はじめに
タイトルにある「機械的メタマテリアル(またはアーキテクテッド・マテリアル)って何ですか?」と、今回ご紹介する材料・構造の研究をされている方に質問してみてください。(ほぼ間違いなく)研究者の方によって答えが異なると思います。
近年、応用物理や機械工学の分野を中心に研究が盛んに行われている「機械的メタマテリアル」ですが、少し論文を調べると「周波数バンド構造」や、「ソリトン波」、「負のポアソン比」など、いろいろな情報が出てきます。(よくわからないけど)これまでの材料・構造とは何か違うという印象を持たれる方が多いと思います。(現在の私の理解だと)機械工学だけでなく他の様々な分野の知見を構造・材料の研究分野に取り入れ、発展してきた経緯があるため、研究者の数だけ「多様な」機械的メタマテリアルの研究があると考えています。本稿では、機械構造に焦点を当て、機械的メタマテリアルにはどんなものがあるのか、宇宙の分野にどんな関係があるのか、そして現在進めている研究についてお話したいと思います。
機械的メタマテリアルにはどんなものがあるのか?
「機械的メタマテリアルとは何か?」を1つの答えに絞るのは難しいので、ここでは「メタマテリアルにはどんなものがあるのか?」についてご紹介しようと思います。機械構造で構成されるメタマテリアル(つまり機械的メタマテリアル)に焦点を当てると、構造全体をユニットセルと呼ばれる要素の周期的な配置で構成し、ユニットセルの幾何形状を工夫することなどで、それを構成する材料自体では発現しない特性を生み出す構造、と捉えて研究をすることがあります(ちなみに、メタマテリアル(metamaterial)の「meta」の接頭語は「超越」を意味します)。このように捉えるのはあくまで一例なので、他にも様々な機械的メタマテリアルの定義はあります。
図1:機械的メタマテリアルの例。(a)ハニカム構造。(b)ラティス構造。また、折り紙に基づく機械的メタマテリアルの例として、(c)吉村パターン、(d)ミウラ折り、(e)Tachi-Miura多面体。
では、どのような構造を機械的メタマテリアルと呼んでいるのか、図1にいくつかの例を挙げてみました。図1(a)のハニカム構造は六角形を敷き詰めた構造で、軽量でかつ高強度など、形状を工夫することで機械的な特性向上を図る、機械的メタマテリアルの良い例かと思います(応用例としてはロケットフェアリング[1] 等)。次に、ラティスと呼ばれる梁のような部材で格子を形作る構造(図1(b))が挙げられます。幾何形状が複雑ですが、3Dプリンターの登場もあり、製作できるようになってきたことで、研究が広く行われています。最近だと、小型月着陸実証機SLIMの着陸脚の衝撃吸収材としてラティス構造が採用されました[2]。
また、こんなものも機械的メタマテリアルになるの?と思われることが多いのが、「折り紙」。実は、近年「Origami-based metamaterials」として研究が盛んに行われています。この「折り紙」の研究ですが、有名なものとして航空機の胴体のような薄い円筒が座屈したときに現れる形状の「吉村パターン」があり、潰れて強くなるという特徴から飲料の缶に応用されています(図1(c))[3]。この吉村パターンは円筒ですが、平面的な形状で有名なのが「ミウラ折り」です(図1(d))[4]。端と端を持って広げるとそれとは対角の方向にも開いていく(その逆の閉じるときも同様)という開きやすい(または閉じやすい)という特徴をもち、地図の折り方やさらにはソーラーアレイといった幅広い応用例があります。円筒の軸方向における座屈の吉村パターン、2次元的に展開・収納するミウラ折り、の他に例えば3次元の空間充填の特性を持ち且つ折り畳める折り紙はあるのか?ということで、本稿では、そのような折り紙の1つとして、私がこれまで研究してきた「Tachi-Miura 多面体」(図1(e))[5] について少し詳しく見ていこうと思います。
折り紙の「形状」と「機械特性」の関係
「折り紙」はこれまでにも工学への応用を目指した研究は多く、IKAROSに代表されるように小さく畳んでおき、使うときに大きく広げるといった例が挙げられます。近年では、「機械的メタマテリアル」の研究の流れと合流することで、「折り紙」が持つ様々な性質が報告されるようになって来ました。Tachi-Miura多面体と呼ばれるミウラ折りを発展させた空間充填の特性を持つ折り紙を例に、従来の材料・構造とはちょっと異なる性質に関する私の研究を紹介します。
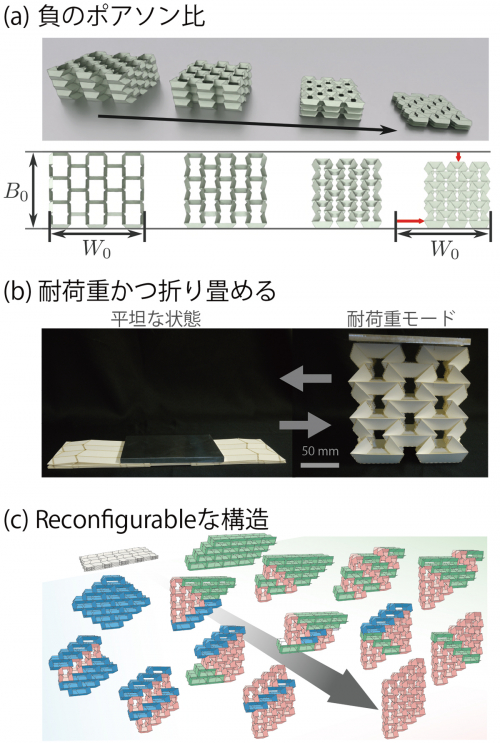
図2:Tachi-Miura多面体の様々な特性。(a)折り畳まれたときの断面形状の変化。(b)紙で試作したモデルの「平坦な状態」と「荷重を支えるモード」の切り替え[7]。(c)1つの折り紙構造が、様々な形状に変化可能な様子を表す図。
1) 負のポアソン比:一般的には材料を潰すと断面が大きくなることが多いです。このような力を加えた縦方向および横方向の変形の比がポアソン比ですが、通常はこの値は正の値を取ります。このポアソン比が負になることは無いのでしょうか?実は、Tachi-Miura多面体は、うまくデザインパラメータを選ぶと、図2(a)のように潰した際に断面が小さくなるように変形するという、ちょっと普通とは違う挙動を示す構造の1つとなることがわかりました[6]。
2) 耐荷重かつ折り畳める:「耐荷重(荷重を支える)」にはがっしりした構造が、「折り畳める」には柔軟に変形できる構造が必要で、その2つは相反する印象があります。Tachi-Miura多面体では、折り目に沿って折っていくことで形状が変化していくのですが、連続的に折り畳まれる途中に2つのモードに分岐する挙動を作り出すことで、特定の方向に関して、ある状態を超えて折ると、図2(b)のように上に物をおいても支えられるようになります。この荷重を支えられる状態(耐荷重モード)は、折り目を何かでロックしているわけではないので、別の方向から引っ張ると先程の平坦な状態にまた折りたたむことが容易にできます[7]。このような構造を用いると「折り畳めて」かつ「荷重も支える」という2つの相反した特性を1つの構造で実現でき、宇宙で空間を持った構造・建築に応用できる可能性を秘めているのではと考えています。
3) Reconfigurableな構造:形状の変形をコントロールしてポアソン比を負にしたり、耐荷重と折畳みを両立させたりできることがわかると、今度は形状をどれくらい自在にコントロールできるのかが気になるかと思います(少なくとも私は気になりました)。このTachi-Miura多面体は、図2(c)左上にある平坦な状態から同図右下の赤い状態に本来折り畳まれます。しかし、折り目を選択的に山折りと谷折りを入れ替えたりなどすると、構造の特定箇所の形状を変更させることができ、構造を製作した後でも、再度作り直すことなく(形状変更の2パターンは図中青色および緑色で示す箇所に対応)、図中の様々な形状に変化可能なことがわかりました(図2(c))[8]。従来のように用途ごとに別々に構造をつくるのではなく、1つの構造を作っておいて、使う目的に応じて変形させ、目的が変わったら、また変形させるといった再使用可能な構造に繋がるかも?と考えています。
金属3Dプリンターを使った折り紙構造
折り紙に基づく機械的メタマテリアルが持つ様々な特性が私を含めた多くの研究者によって研究されてきました。しかし、宇宙機などへの工学応用を考えた時に、「紙」以外の材料(特に金属)でも作れるのか?金属で作った場合、紙で作ったときと同じ挙動になるのか?など、課題はたくさんあります。そういった課題へのアプローチとして、(私の)JAXAでの研究では金属3Dプリンターを活用した折り紙構造の製作に取り組んでいます。折り「紙」ではなく、折り「金属」です。ただし、シート状の材料に折り目を入れて、3次元構造に折っていくのではなく、ここでは最終的な3次元形状を直接プリントしていきます。JAXA安全・信頼性推進部の境野 正法さんとNTT データザムテクノロジーズ様にご協力いただき、アルミ合金を使って手のひらサイズの大きさのプロトタイプを作りました(本号の表紙の図)。
ISASニュース 2024年4月号表紙図:機械的メタマテリアル・金属 3Dプリンターを融合させた新しい構造の探求
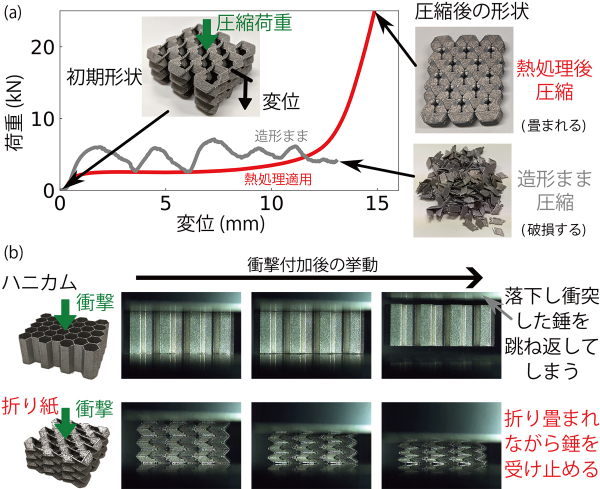
形状がうまく作れたら、折り紙のように折りの動きを出すのは簡単かというと、実はそうでもありませんでした。構造の初期状態を表紙の図下段として、本来のTachi-Miura多面体の潰れる(折り畳まれる)変形は図1(e)右下のようになるのですが、3Dプリンターで造形したままのものを潰すと、図3(a)右下のように理想の折り畳まれた形状とはかけ離れた状態に...(折り目に沿って壊れ、粉々になってます)。そこで、3Dプリントした後に、ある条件で熱処理をし圧縮をすると、圧縮後の形状は本来のTachi-Miura多面体の畳まれた状態(図3(a)右上)と同じように、綺麗に折り畳まれて潰れているのがわかるかと思います。
この「紙のように綺麗に折れる」というのを衝撃吸収に活かせるのでは?というので、衝撃試験をしてみました。比較用にTachi-Miura多面体と同じ材料・同じ体積のハニカムを作り、同じ衝撃を加えると、ある衝撃の大きさではハニカムは(面外方向に)あまり潰れず、衝撃を加えるために上から落としたインパクターが跳ね返ってしまいました(図3(b)上段)。一方、Tachi-Miura多面体は綺麗に折れることでスムーズにエネルギーを吸収できているのがわかります(図3(b)下段)[9]。まだ金属3Dプリンターを使った折り紙構造の研究は少なく、始まったばかりですが、折り紙の折り挙動による、圧縮を受けた構造の変形をコントロールできる利点を活かした衝撃吸収機構、折り紙の形状可変な特性を用いた宇宙での展開構造(または建築物)など様々な応用ができるのでは?とワクワクしながら研究を進めているところです。
図3:金属3Dプリンターで製作した折紙に基づく機械的メタマテリアル[9]。(a)アルミ合金を用いて試作した折紙の(準静的)圧縮試験結果と、造形ままおよび熱処理を適用後に圧縮した場合の圧縮後の状態。(b)同じ体積を持つハニカムと折紙の衝撃試験を行ったときの様子。
さいごに
折り紙を使った機械的メタマテリアルを中心に様々な面白い特性や応用への可能性についてご紹介させていただきましたが、この他にも色々なメタマテリアルの研究が行われています。冒頭の「機械的メタマテリアルとは何か?」の答えが研究者の数だけあると曖昧な言い方をしましたが、多様な分野の知見を取り入れ、それらを機械構造へ適用することで構造というものを理解・解析・設計しようと様々な角度からアプローチした結果の裏返しとも捉えることができるのかなとも私は思います。また、機械的メタマテリアルのような新しい構造材料の設計手法と、3Dプリンターといった新しい製造技術を融合することで、宇宙分野を含めた様々な産業への応用が期待できるのではと考えます。
参考文献
[1] JAXA 宇宙輸送技術部門. ロケットの基礎知識.
https://www.rocket.jaxa.jp/column/knowledge/fairing.html
[2] 河野太郎, 小型月着陸実証機SLIMの着陸機構, 宇宙科学最前線, 読むISAS.
https://www.isas.jaxa.jp/feature/forefront/191226.html
[3] 三浦公亮, 「考証:チューハイ缶と宇宙研の関係」, 2002年9月号いも焼酎.
https://www.isas.jaxa.jp/j/isasnews/backnumber/2002/ISASnews258.pdf
[4] Miura, K. Method of packaging and deployment of large membranes in space. The Institute of Space and Astronautical Science Report No.618 1-9 (1985).
[5] Tachi, T. & Miura, K. Rigid-Foldable cylinders and cells. Journal of the International Association for Shell and Spatial Structures 53, 217-226 (2012).
[6] Yasuda, H. & Yang, J. Reentrant origami-based metamaterials with negative Poisson's ratio and bistability. Physical Review Letters 114, 185502 (2015).
[7] Yasuda, H., et al. Origami‐based cellular structures with in situ transition between collapsible and load‐bearing configurations. Advanced Engineering Materials 21, 1900562 (2019).
[8] Miyazawa, Y. et al. Heterogeneous origami-architected materials with variable stiffness. Communications Materials 2, 110 (2021).
[9] Yasuda, H. & Kunimine, T. Energy absorption of AlSi10Mg origami cellular structures fabricated via laser powder bed fusion. MRS Communications 1-7 (2024).
https://doi.org/10.1557/s43579-024-00518-7
【 ISASニュース 2024年4月号(No.517) 掲載】