TOP > レポート&コラム > 宇宙科学の最前線 > 惑星間航行・編隊飛行のための宇宙機軌道設計


複数フライバイ軌道の設計
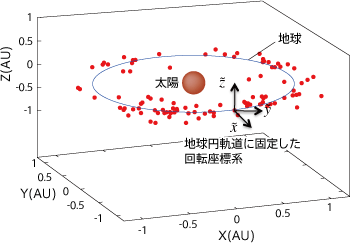
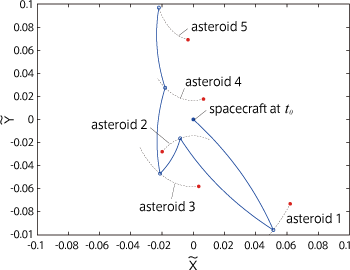
「母関数」の理論を使うと、今までは計算上不可能であった複数の小惑星を次々と通過する軌道(複数フライバイ軌道)の最適化の計算時間を大幅に減らすことができます。例えば、図2Aのような地球近傍の100個の小惑星の中から必要な速度変化量が最小になるような5つの対象と訪れるべき順番を決め、一定の時間おきに小惑星を通過する軌道を設計しようとすると、全部で9,034,502,400通りの順列組み合わせに対してランベール問題を解いて、最適なものを選び出さなければいけません。母関数を使うと、時間間隔さえ固定してしまえば、必要な総速度変化量を計算するための計算式を求めることができます。このため、その計算式に境界条件を代入して必要な総速度変化量を計算すれば、最適なもの、すなわち総速度変化量が小さくて燃料消費が少ない軌道を、現実的な計算時間で見つけることができます(図2B)。従来の設計方法では、初めに対象や行く順番を決めてしまってから燃料消費が最小となるような行き方を決めるので、時間間隔は設計パラメータになります。しかし母関数の方法では、時間間隔を固定することで最適化を可能にしているので、時間間隔の設計には注意が必要となります。
このほかにも、母関数をうまく使うことで、低推力連続加速宇宙機の軌道最適化といった、より難しい問題にも応用できることが分かっています。
|
![]()