Video: The lead author Ryan Lau introduces the highlights of the research results. (Credit: NAOJ and ISAS/JAXA)
With almost two decades of mid-infrared (IR) imaging from the largest observatories around the world including the Subaru Telescope, a team of astronomers was able to capture the spiral motion of newly formed dust streaming from the massive and evolved binary star system Wolf-Rayet (WR) 112. Massive binary star systems, as well as supernova explosions, are regarded as sources of dust in the Universe from its early history, but the process of dust production and the amount of the ejected dust are still open questions. WR 112 is a binary system composed of a massive star in the very late stage of stellar evolution losing a large amount of mass and another massive star at the main sequence. Dust is expected to be formed in the region where stellar winds from these two stars are colliding. The study reveals the motion of the dusty outflow from the system and identifies WR 112 as a highly efficient dust factory that produces an entire Earth mass of dust every year.
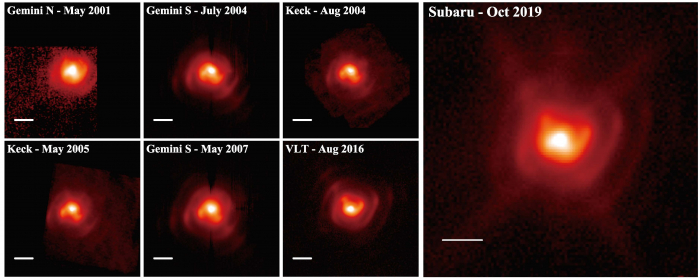
Figure 1: Sequence of 7 mid-IR (~10 micrometers) images of WR 112 taken between 2001 - 2019 by Gemini North, Gemini South, Keck, the Very Large Telescope (VLT), and the Subaru Telescope. The length of the white line on each image corresponds to about 6800 astronomical units. (Caption for the supplementary figure: "Spurs" are the structures formed in the past 20 years showing variations between observations. "Nested shells" are expanding structures formed previously. The X-like signature in the image from the Subaru Telescope is an artifact due to the properties of the instrument.) (Credit: Lau et al.)
Dust formation, which is typically seen in the gentle outflows from cool stars with a Sun-like mass, is somewhat unusual in the extreme environment around massive stars and their violent winds. However, interesting things happen when the fast winds of two massive stars in a binary interact.
"When the two winds collide, all Hell breaks loose, including the release of copious shocked-gas X-rays, but also the (at first blush surprising) creation of copious amounts of carbon-based aerosol dust particles in those binaries in which one of the stars has evolved to He-burning, which produces 40% C in their winds," says co-author Anthony Moffat (University of Montreal). This dust formation process is exactly what is occurring in WR 112. (Note 1)
This binary dust formation phenomenon has been revealed in other systems such as WR 104 by co-author Peter Tuthill (University of Sydney). WR 104, in particular, reveals an elegant trail of dust resembling a 'pinwheel' that traces the orbital motion of the central binary star system (see http://www.physics.usyd.edu.au/~gekko/pinwheel/movie_11.gif)
However, the dusty nebula around WR 112 is far more complex than a simple pinwheel pattern. Decades of multi-wavelength observations presented conflicting interpretations of the dusty outflow and orbital motion of WR 112. After almost 20 years uncertainty on WR 112, images from the COMICS instrument on the Subaru Telescope taken in Oct 2019 provided the final--and unexpected--piece to the puzzle.
"We published a study in 2017 on WR 112 that suggested the dusty nebula was not moving at all, so I thought our COMICS observation would confirm this," explained lead author Ryan Lau (ISAS/JAXA). "To my surprise, the COMCIS image revealed that the dusty shell had definitely moved since the last image we took with the VLT in 2016. It confused me so much that I couldn't sleep after the observing run--I kept flipping through the images until it finally registered in my head that the spiral looked like it was tumbling towards us."
Lau collaborated with researchers at the University of Sydney including Prof. Peter Tuthill and undergraduate Yinuo Han, who are experts at modeling and interpreting the motion of the dusty spirals from binary systems like WR 112. "I shared the images of WR 112 with Peter and Yinuo, and they were able to produce an amazing preliminary model that confirmed that the dusty spiral stream is revolving in our direction along our line of sight," said Lau.
Animation 1: Animated model of the spiral dust nebula around WR 112 (left) and the actual corresponding observations (right). The φ symbol on the model animation indicates the orbital phase of the central binary, where φ = 0 is at the beginning of its 20-yr orbit, and φ = 1 is at the end of its orbit. The animation pauses at each phase that is displayed in the real observations. (Credit: Lau et al.)
The animation above shows a comparison between the models of WR 112 created by the research team alongside the actual mid-IR observations. The appearance of the model images shows a remarkable agreement with the real images of WR 112. The models and the series of imaging observations revealed that the rotation period of this dusty "edge-on" spiral (and the orbital period of the central binary system) is 20 years.
The drastic difference between "face-on" vs "edge-on" appearance, which has to do with our viewing angle of WR 112, is demonstrated in the figure and animations below.
Figure 2: Model of the WR 112 nebula from a face-on viewing angle (left) and the observed viewing angle (right). The dashed lines illustrate the motion of the central binary orbit, where the separation of the central binary and size of each star is not shown to scale. Each panel has its own accompanying animation that shows the revolution of the spiral in both viewing angles. (Credit: Lau et al.)
Animation 2a
Animation 2b
The animation below helps to visualize the transition from the face-on to the observed viewing angle of WR 112.
Animation 3: This animation shows the effect of viewing angle on the appearance of the dusty spiral. First, the "face-on" model shows one full revolution of the dusty spiral if it were rotating in the plane of the sky. The spiral is then rotated to the observed inclination (i) and rotation angle (Ω), where it proceeds with another full revolution. Note that the geometry of the 3D spiral itself is the exact same, but it's only the viewing angle that changes its appearance. (Credit: Lau et al.)
With the revised picture of WR 112, the research team was able to deduce how much dust this binary system is forming. "Spirals are repetitive patterns, so since we understand how much time it takes to form one full dusty spiral turn (~20 years), we can actually trace the age of dust produced by the binary stars at the center of the spiral," says Lau. He points out that "there is freshly formed dust at the very central core of the spiral, while the dust we see that's 4 spiral turns away is about 80 years old. Therefore, we can essentially trace out an entire human lifetime along the dusty spiral stream revealed in our observations. So I could actually pinpoint on the images the dust that was formed when I was born (right now, it's somewhere in between the first and second spiral turns)."
To their surprise, the team found WR 112 is a highly efficient dust factory that outputs dust at a rate of 3x10-6 solar mass per year, which is equivalent to producing an entire Earth mass of dust every year. This was unusual given WR 112's 20-yr orbital period--the most efficient dust producers in this type of WR binary star system tend to have shorter orbital periods less than a year like WR 104 with its 220-day period. WR 112 therefore demonstrates the diversity of WR binary systems that are capable of efficiently forming dust and highlights their potential role as significant sources of dust not only in our Galaxy but galaxies beyond our own.
Lastly, these results demonstrate the discovery potential of multi-epoch mid-IR imaging with the MIMIZUKU instrument on the upcoming Tokyo Atacama Observatory (TAO). The mid-IR results from this study notably utilize the largest observatories in the world and set the stage for the next decade of astronomical discoveries with 30-m class telescopes and the upcoming James Webb Space Telescope.
These research results were published as Ryan M. Lau et al. "Resolving Decades of Periodic Spirals from the Wolf-Rayet Dust Factory WR 112" on September 15, 2020 in The Astrophysical Journal.
(Note 1) Wolf-Rayet (WR) stars are evolved very massive stars that have already lost their hydrogen-rich envelope. The surface of these objects is rich in heavy elements like carbon produced by the internal helium burning process. This results in the ejecta from WR stars including high fractions of carbon and other heavy elements, in contrast to the hydrogen-rich material ejected by usual evolved stars, forming a large amount of dust.

![[Figure 2]](/en/topics/assets_c/2020/09/20200916_2-thumb-700xauto-7809.jpg)