変換行列は9つの要素を持つわけだが、独立な要素は3つである。これは、 オイラーの定理より、任意の直交変換は回転軸の方向(2つの変数で決まる) とそのまわりの回転角(3つめの変数)を与えれば実現できることから理解できる。 その3つの変数を指定すれば、二つの座標系の間の変換を一意的に定義したことになる。
座標変換を表わす3つのパラメーターとして良く使われるものにオイラー角 がある。オイラー角にもいろいろな定義があるが、ここでは日本の科学衛星の姿勢に使われている 「zyz」オイラー角の定義を用いて議論を進める。
赤道座標の上で、2.3節で定義した、![]() 軸を考える(
軸を考える(![]() 軸は春分点、
軸は春分点、
![]() 軸は北極を向いている)。たとえばこれが人工衛星の三軸だったら、今から定義する
オイラー角は人工衛星の姿勢を与えることになるし、別の座標軸だったら、
オイラー角は異なる天球座標系の間の変換を与える。
軸は北極を向いている)。たとえばこれが人工衛星の三軸だったら、今から定義する
オイラー角は人工衛星の姿勢を与えることになるし、別の座標軸だったら、
オイラー角は異なる天球座標系の間の変換を与える。
![]() 軸の周りに、
軸の周りに、![]() の向きを向いて時計周りに角度
の向きを向いて時計周りに角度![]() 回転し、
回転し、
![]() 軸、
軸、![]() 軸の位置を変える。この新たな3軸を、便宜上
軸の位置を変える。この新たな3軸を、便宜上![]() としよう(
としよう(![]() である)。
次に、
である)。
次に、![]() 軸の周りに、角度
軸の周りに、角度![]() 回転し、
回転し、![]() 軸の
位置を変え、
軸の
位置を変え、![]() 軸を定義する(
軸を定義する(![]() である)。最後に、
である)。最後に、![]() 軸の周りに
軸の周りに![]() 回転し、
最終的に、
回転し、
最終的に、![]() ,
,![]() ,
,![]() 軸を定義することができる。
軸を定義することができる。![]() 軸による旧座標系と、
軸による旧座標系と、![]() 軸による
新座標系の間の関係を与える
軸による
新座標系の間の関係を与える
![]() を、オイラー角と呼ぶ。
を、オイラー角と呼ぶ。
このように定義したオイラー角と、(19)または(28)で与えられる変換行列との関係を調べてみよう。まず、最初の![]() 軸のまわりの
軸のまわりの![]() 回転で、新たな
基底ベクトルと元の基底ベクトルの間の関係は以下のようになる。
回転で、新たな
基底ベクトルと元の基底ベクトルの間の関係は以下のようになる。
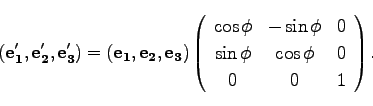 |
(50) |
同様にして、![]() 軸周りの
軸周りの![]() 回転によって、
回転によって、
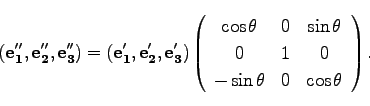 |
(51) |
![]() 軸周りの
軸周りの![]() 回転によって、
回転によって、
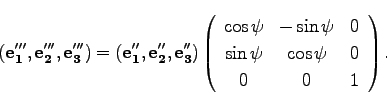 |
(52) |
以上、3式をまとめて、
これが、このノートの冒頭で与えた式(6)である。
これは回転行列だから、条件(34)と(42)を満たしていることに注意しよう![]() 。
。