



Next: 座標変換の計算
Up: 回転による座標変換
Previous: 直交変換と変換行列
Contents
直交変換の簡単な記法
直交行列の性質を簡単に表す記法がある。まず、添字、1,2,3,4を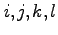 などの文字で表す。
Kroneckerのデルタを導入する。
などの文字で表す。
Kroneckerのデルタを導入する。
 |
(31) |
さらに、「同じ添字が対になって一つの項に現われるときには、常にその添字について1から3まで (3次元空間の場合)あるいは
1から4まで(4次元時空の場合)の和を
とる( 記号を省略する)」という総和の規約を導入する。
すると、
基底ベクトルの直交条件、(14),(15)は以下のように書ける。
記号を省略する)」という総和の規約を導入する。
すると、
基底ベクトルの直交条件、(14),(15)は以下のように書ける。
 |
(32) |
二つの座標系の基底ベクトルと、変換行列との関係は以下のようになる。
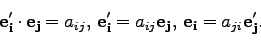 |
(33) |
座標軸の直交関係を表わす(20),(21),(29),(30)は、
 |
(34) |
となる。
Ken EBISAWA
2011-05-30
