



Next: 直交変換の簡単な記法
Up: 回転による座標変換
Previous: 方向ベクトルと座標変換
Contents
基底ベクトル
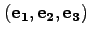 で表される直交座標系と
で表される直交座標系と
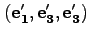 で表される直交座標系の間の直交変換を考える(添字1,2,3が
上で書いた
で表される直交座標系の間の直交変換を考える(添字1,2,3が
上で書いた に対応)。
これらは、それぞれ互いに垂直な単位ベクトルの組だから、
に対応)。
これらは、それぞれ互いに垂直な単位ベクトルの組だから、
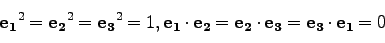 |
(14) |
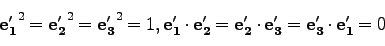 |
(15) |
片方の系のベクトルはもう片方の系のベクトルを使って表わすことができる。
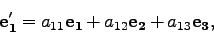 |
(16) |
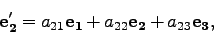 |
(17) |
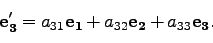 |
(18) |
行列表示すると、
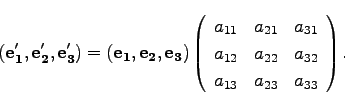 |
(19) |
(15)の条件より、この変換行列の各要素の間に、
 |
(20) |
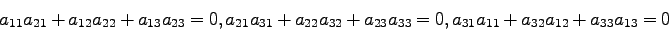 |
(21) |
が成立する。
また、(16)、(17)、(18)と、
 の内積を取ることにより、以下がわかる。
の内積を取ることにより、以下がわかる。
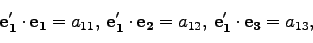 |
(22) |
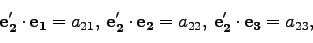 |
(23) |
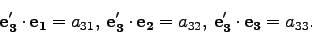 |
(24) |
つまり、式(19)
で定義される変換行列の9つの変換係数は旧座標系の3軸と新座標系の3軸の間の
なす9つの角度の余弦に対応している。これを、「
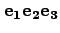 で表わされる系に
おける
で表わされる系に
おける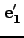 ,
,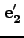 ,
,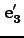 の方向余弦は、それぞれ
の方向余弦は、それぞれ
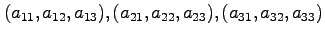 である」、という言いかたをする。同様に、
式(22),(23),(24)を縦に眺めると、
「
である」、という言いかたをする。同様に、
式(22),(23),(24)を縦に眺めると、
「
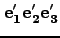 で表わされる系に
おける
で表わされる系に
おける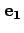 ,
,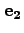 ,
,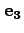 の方向余弦は、それぞれ
の方向余弦は、それぞれ
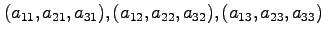 である」
ことがわかる。
である」
ことがわかる。
よって、
式(16),(17),(18)
の逆変換は、
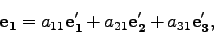 |
(25) |
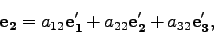 |
(26) |
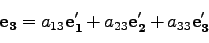 |
(27) |
となる。
行列表示すると、
 |
(28) |
(14)の条件より、(20), (21)に対応する式は、
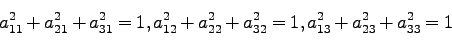 |
(29) |
、
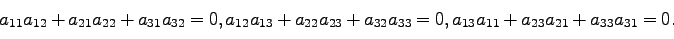 |
(30) |
式(19)と式(28)を比較すると、変換行列の
行と列を入れかえた転置行列が逆行列になっていることがわかる。




Next: 直交変換の簡単な記法
Up: 回転による座標変換
Previous: 方向ベクトルと座標変換
Contents
Ken EBISAWA
2011-05-30