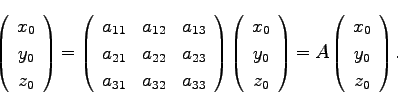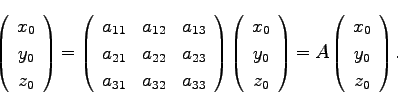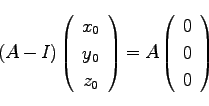Next: オイラー角
Up: オイラー角と座標変換
Previous: オイラー角と座標変換
Contents
今、共通の原点を持つ二つの直交座標系の間の座標変換(点のまわりの回転変位)を考えているのだが、この場合に以下の
オイラーの定理が成立する。
定理 I
点のまわりの回転変位は、その点を通る1つの軸のまわりの回転によって達っせられる。
これを、すでに学んだ直交行列の性質から簡単に証明することができる。回転変位を実現する回転軸に沿った方向ベクトル
はその変換によって不変だから、そのベクトルの3成分を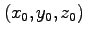 と書けば、
と書けば、
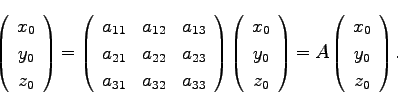 |
(44) |
ここで変換行列を単純に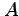 と書いた。これは、直交行列
と書いた。これは、直交行列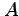 に対して、
に対して、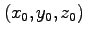 が
固有ベクトルであり、固有値が1であることを示している。
単位行列
が
固有ベクトルであり、固有値が1であることを示している。
単位行列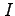 を持ちいると、上式は、
を持ちいると、上式は、
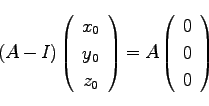 |
(45) |
と書ける。つまり、行列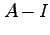 には逆行列が存在しない。その条件は、行列式が0であること、
には逆行列が存在しない。その条件は、行列式が0であること、
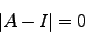 |
(46) |
である。ところで、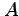 の転置行列
の転置行列
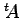 は
は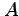 の逆行列だから、
の逆行列だから、
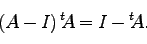 |
(47) |
ここで両辺の行列式を取り、転置行列の行列式は元の行列式と等しいこと、回転行列の
行列式は1であること(式42)を持ちいると、
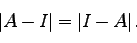 |
(48) |
一般に、 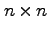 行列
行列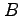 の行列式について、
の行列式について、
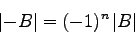 |
(49) |
が成立する。今考えている3次元行列については、
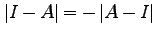 である。よって、
(48)は(46)を示していることがわかる。
である。よって、
(48)は(46)を示していることがわかる。
Ken EBISAWA
2011-05-30