



Next: オイラー角と座標変換
Up: 回転による座標変換
Previous: 座標変換の計算
Contents
もうひとつ、直交行列の性質として、その行列式の値は1である、と言うことがある。
これを証明してみよう。
まず、ベクトルの外積の復習をしておこう。
3次元のベクトル
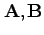 の外積を
の外積を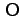 とする
とする![[*]](file:/usr/local/share/lib/latex2html/icons/footnote.png) 。
。
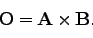 |
(37) |
Oは、AからBの向きに右ネジを回したときに、ネジが進む方向を
向くベクトルで、その大きさは、AとBがなす角を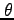 とすると、
とすると、
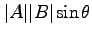 で与えられる (
で与えられる ( と
と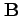 を二辺とする平行四辺形の面積)。また、各成分は以下の通りである。
を二辺とする平行四辺形の面積)。また、各成分は以下の通りである。
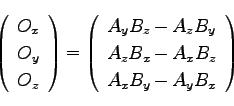 |
(38) |
一般的に、ベクトル
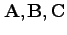 のスカラー三重積は、
のスカラー三重積は、
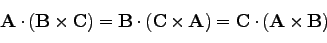 |
(39) |
で定義される。
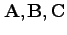 がこの順に右手系をなすとき、スカラー三重積は、
この3つのベクトルが作る平行六面体の体積を表わす。 スカラー三重積を
がこの順に右手系をなすとき、スカラー三重積は、
この3つのベクトルが作る平行六面体の体積を表わす。 スカラー三重積を
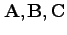 の直角成分を用いて書くと、
の直角成分を用いて書くと、
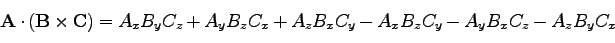 |
(40) |
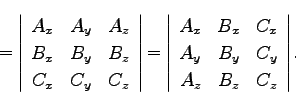 |
(41) |
ここで、
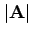 は行列
は行列 の行列式を示す。
上記で定義した直交座標系の基底ベクトル
の行列式を示す。
上記で定義した直交座標系の基底ベクトル
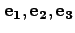 または
または
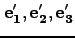 が作る平行六面体の体積は当然1なので、
それらのスカラー三重積は1、つまり直交変換の変換行列の行列式の値は1である。
が作る平行六面体の体積は当然1なので、
それらのスカラー三重積は1、つまり直交変換の変換行列の行列式の値は1である。
 |
(42) |
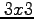 行列の行列式の計算方法から
行列の行列式の計算方法から
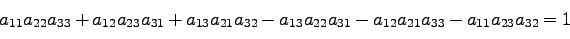 |
(43) |
である。
Ken EBISAWA
2011-05-30
![]() の外積を
の外積を![]() とする
とする![]() 。
。
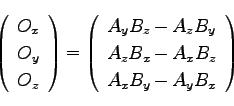
![]() のスカラー三重積は、
のスカラー三重積は、
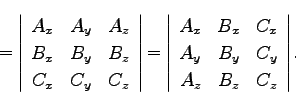
![]() 行列の行列式の計算方法から
行列の行列式の計算方法から