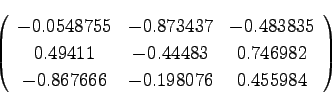3次元空間、4次元時空の回転の例

ここでは、大学一年で学ぶ初歩的な線形代数の応用例として3次元空間、4次元時空の座標系の回転を考えてみよう。 それによって、特殊相対性理論を理解することを目標とする。

以下に3つの行列を示す。これらの行列に共通の特徴を読み取れるだろうか？

$$\left(\begin{array}{ccc} -0.0548755 & -0.873437 & -0.483835\... ...982\\ -0.867666 & -0.198076 & 0.455984\\ \end{array}\right)$$ (5)

$$\left(\begin{array}{ccc} \cos \phi \cos\theta \cos \psi - \... ...si & \sin \theta \sin \psi & \cos \theta\\ \end{array}\right)$$ (6)

$$\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\... ...a /\sqrt{1-\beta^2}& 1/\sqrt{1-\beta^2} \\ \end{array}\right)$$ (7)

これらの行列は、

1. 各列あるいは各行を成分とするベクトルの長さが1(自分自身との内積が1)
   
2. 各列あるいは各行を成分とするベクトルは、他の列あるいは行を成分とする ベクトルと直交している(内積が0)
   

という特徴がある(実際に確かめてみよう)。 このような行列を直交行列と呼ぶ。 直交行列は二つの座標系の間の、回転による座標変換を記述する。

3次元空間に任意の座標系をとり、 位置ベクトル$(x,y,z)$を考える。その座標系を回転させて、新たな位置ベクトルが$(x',y',z')$ となったとする。回転によってベクトルの長さが変わらない事は直感的にわかるだろう。 つまり、

$$x^2+y^2+z^2=x'^2+y'^2+z'^2$$ (8)

である。直交行列による座標変換は、ベクトルの長さを変えない、という 特徴がある。その条件を正確に書き出すと、上記の二つの条件になる。

冒頭に示した3つの行列の物理的意味は何であろうか？(5)は、天空上の赤道座標から 銀河座標への 座標変換を表す。 (6)は、人工衛星の姿勢が $(\phi,\theta, \psi)$ のオイラー角で表されるとき、人工衛星上の座標と天球座標の間の変換を与える。 (7)は、静止している座標系とそれに対して速度$\beta=v/c$ ($c$は光速; よって$\beta \leq 1$) で等速運動している座標系の間のローレンツ変換を与える。二つの等速運動している座標系の間で、 モノの長さや時間は保存されないことに注意しよう (時間や長さは伸び縮みする！)。保存されるのは、四次元時空における世界距離なのである(これが特殊相対性理論の本質!)。

これら3つの物理的には全く異なる状況が、全く同じ数学で記述される事がポイントである。これらについて、以下に順に解説していく。