Evaluation of spectral resolving power of an immersion-echelle high-dispersion spectrometer using mid-infrared wave tracing calculations
Jun. 29, 2022 | GATEWAY to Academic Articles
Immersion echelle gratings are small, high-dispersion elements used in optical-infrared astronomy for high wavelength-resolution spectroscopic observations of celestial objects. However, the commonly used evaluation formula for the wavelength resolution of immersion echelle gratings for point sources does not consider the effects of diffraction at two locations: the entrance slit and the finite-size window of the immersion echelle grating. This study realized a calculation that traces the propagation of light waves and evaluated the spectral resolving power of the mid-infrared immersion-echelle spectrometer. The main result was that the presence of an entrance slit reduces the effect of telescope aberrations on the spectral resolving power. In addition, when the slit width was varied for realistic grating sizes, we found that the minimum spectral resolving power emerged at the seemingly optimal slit width, where the slit transmits the entire width of the main lobe of the incident beam. We expect these findings to be helpful for the design of future high-wavelength-resolution mid-infrared spectrographs and space telescopes that include such spectrographs.
Research Summary
Spectroscopic observations with a high spectral resolving power that can detect wavelength deviations smaller than a few tens of thousands of wavelengths in the 10-20 µm infrared band are an unexplored area of observational astronomy and are of great scientific importance.
For example, we can use the Doppler effect of light to determine the position of snow lines*1 in protoplanetary disks*2. H2O gas creates a characteristic peak on the infrared spectra. This peak shape is modified by the Doppler effect of light produced when observing a light source (H2O gas) in motion in the line-of-sight direction. By measuring this peak shape and comparing it to a model that includes disk movements that are close to Kepler's law, the position of the snow line can be identified. This is an important observational verification of current planet formation models.
To make spectroscopic observations of the entire 10-20 µm wavelength band, it is necessary to observe from a space telescope to avoid light absorptions by the atmosphere. In addition, we must cool the entire instrument, including the optics, to cryogenic temperatures to avoid thermal radiation noise from the instrument itself. For these reasons, there are severe requirements on the size of the spectrometer.
Immersion echelle gratings are dispersive elements that enable spectroscopy with a high spectral resolving power in a small size by using diffraction gratings*3 with high diffraction orders in contact with a material with a high refractive index. Therefore, they are promising for the realization of high-wavelength-resolution spectrometers in the 10-20 µm wavelength range.
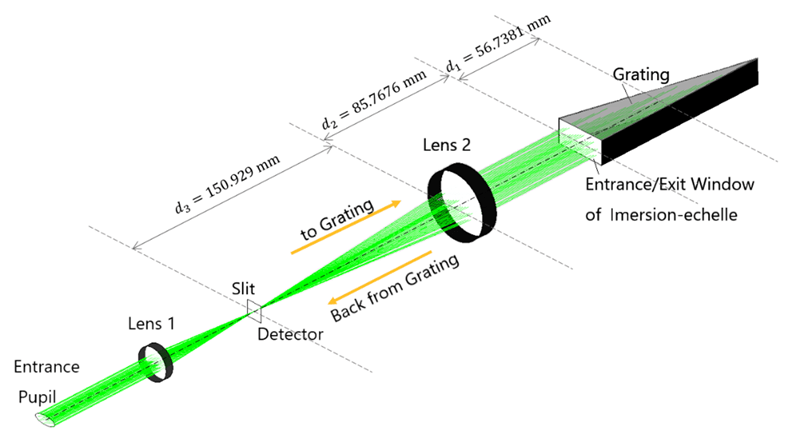
Nevertheless, the evaluation formula for spectral resolving power (R=λ/Δλ; λ is the wavelength consider for the evaluation; Δλ is the minimum resolvable wavelength difference) for a point source of an immersion echelle grating used so far did not consider the effect of light diffraction in two stages at the spectrometer entrance slit and the grating window (See Fig.1 for a schematic of spectrometer setup used in the calculation). In this study, we considered these effects and performed numerical calculations to trace the propagation of light waves. We investigated how the presence or absence of an incident slit, slit width, and optical aberration*3 affect the spectral resolving power of the mid-infrared spectrometer using immersion echelle grating.
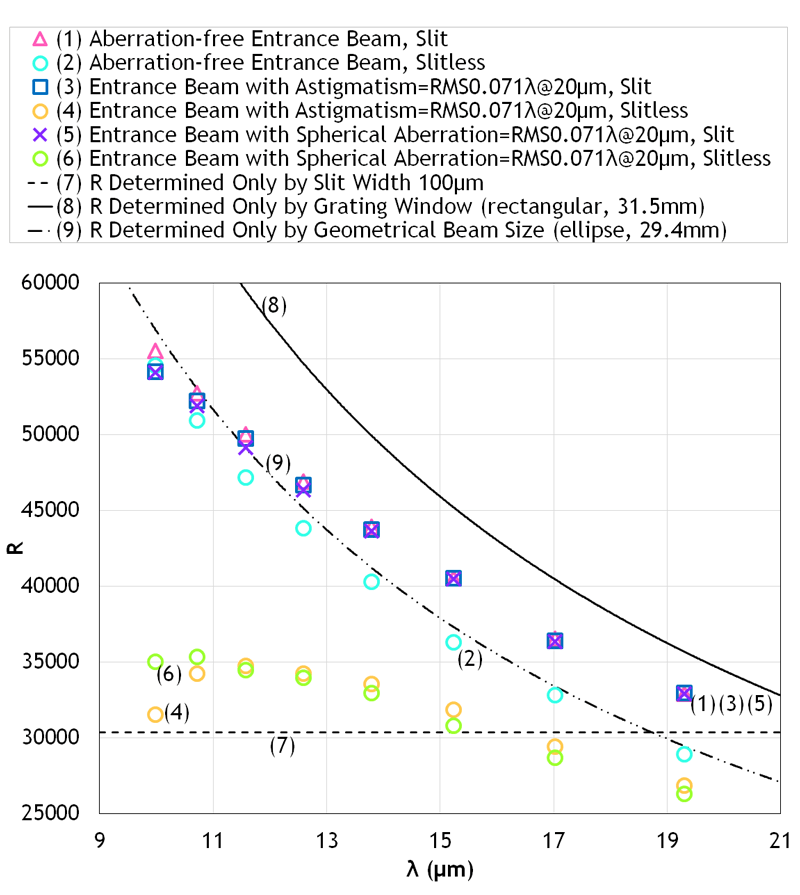
Fig.2 shows the calculated wavelength resolution at various wavelengths and with/without slits and telescope aberration. The vertical axis in Fig.2 is spectral resolving powers. The horizontal axis is wavelengths. As evaluation points, we have chosen wavelengths at which the grating exit rays are exactly the reverse paths of the incident rays (see Fig.1) at various diffraction orders [Fig.2 (1)-(6)]. The amount of telescope aberration assumed was the amount that would result in a Strehl ratio*4 of 80% at a wavelength of 20 μm. The slit width assumed corresponds to the full width at half maximum of the diffraction-limited Point Spread Function*5 at a wavelength of 18.34 μm. From (2), (4), and (6) for the case without a slit, we see that aberrations affect R when there is no slit. On the other hand, from (1), (3), and (5) for the case with a slit, we observe that the presence of the assumed aberration has little effect on R when there is a slit. This means that the presence of the slit relaxes the requirement for the accuracy of the telescope's mirror shape from the perspective of wavelength resolution.
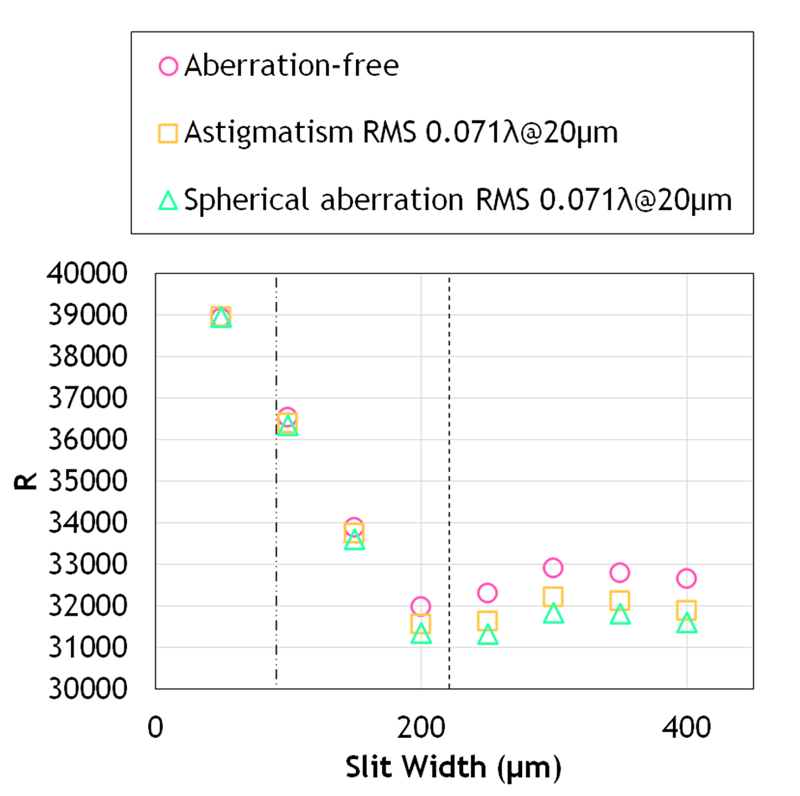
Fig.3 shows calculation results for the same setup, but this time we fixed the wavelength at 17.03 μm and we vary the slit width on the horizontal axis. Fig.3 shows that the wavelength resolution reaches a minimum around a certain slit width, regardless of the assumed aberration. This slit width is approximately the width of the main lobe*6 of the diffraction-limited Point Spread Function. In other words, a slit width that extracts only the main lobe of the Point Spread Function is the design that causes the most loss from the perspective of wavelength resolution. We expect the accumulation of such basic knowledge on instruments to have an impact on the design of future high spatial resolution mid-infrared spectrometers and space telescopes that include such instruments.
Terminologies
- *1 protoplanetary disk : A disk of gas and dust that forms around a newly-forming star. The dust in this disk coalesces to form planets.
- *2 snow line : The position in a protoplanetary disk where water changes from gas to solid (ice).
- *3 diffraction grating : An element that periodically modulates the amplitude or phase of transmitted or reflected light waves in space to create directions in which the waves strengthen and weaken each other. It is used to make spectra of light by utilizing the wavelength dependence of the direction in which the waves strengthen each other. For example, an array of equally spaced slits is diffraction grating. Waves from adjacent slits strengthen each other in the direction where the phase difference between them is m times the wavelength (m is an integer). The m is called the diffraction order.
- *4 optical aberration : A measure that quantifies non-ideality in imaging optics such as lenses and telescopes. The deviation from the spherical surface of the wavefront of the focusing light. We can express the deviation as a superposition of a set of two-dimensional functions, each of which corresponds to a category of aberration (e.g., spherical aberration, astigmatism).
- *5 Strehl ratio : The ratio of the actual intensity of light at the center of focus of an imaging optical system and the intensity of light when we assume the imaging optical system to have no aberration. It expresses the magnitude of aberration.
- *6 point spread function : A function that expresses how the focusing light forms the intensity distribution on the image plane when an imaging optical system collects a point light source at an object point to an image point. Even if an optical system has perfect point-to-point imaging from the perspectives of geometrical optics, the intensity distribution on the image surface will spread due to the diffraction of light waves unless the optical system collects all light emitted from the object point.
- *7 full width at half maximum : A measure of the spread of peak structure when observed data or signals are plotted as a single-variable function graph. It is defined as the interval on the variable axis between two points with half the peak value.
- *8 main lobe : The main lobe means the mountain-shaped region with the highest intensity at the center of the peaks when a beam has multiple peaks due to diffraction.
Information
| Journal Title | Journal of Astronomical Telescopes, Instruments, and Systems |
|---|---|
| Full title of the paper | Simulations of the Spectral Resolving Power of a Compact Space-Borne Immersion-Echelle Spectrometer Using Mid-Infrared Wave Tracing |
| DOI | https://doi.org/10.1117/1.JATIS.8.2.025004 |
| Publish date | 23 June 2022 |
| Author(s) | Satoshi Itoh, Daisuke Ishihara, Takehiko Wada, Takao Nakagawa, Shinki Oyabu, Hidehiro Kaneda, Yasuhiro Hirahara and the SMI consortium |
| ISAS or JAXA member(s) among author(s) |
ITOH Satoshi(Dept. of Space Astronomy and Astrophysics, ISAS), NAKAGAWA Takao(Dept. of Space Astronomy and Astrophysics, ISAS), ISHIHARA Daisuke(Dept. of Space Astronomy and Astrophysics, ISAS), WADA Takehiko(Dept. of Space Astronomy and Astrophysics, ISAS) |


 ITOH Satoshi / Nagoya University (At the time: Dept. of Space Astronomy and Astrophysics, ISAS)
ITOH Satoshi / Nagoya University (At the time: Dept. of Space Astronomy and Astrophysics, ISAS) 