



Next: 楕円軌道
Up: 二体問題
Previous: 換算質量
Contents
地球の周りの人工衛星の軌道や、太陽のまわりの惑星の軌道を考えてみよう。以下で、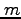 は人工衛星または惑星の換算質量、
は人工衛星または惑星の換算質量、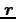 は、
地球中心に相対的な人工衛星の位置、あるいは太陽に相対的な惑星の位置を示す。
は、
地球中心に相対的な人工衛星の位置、あるいは太陽に相対的な惑星の位置を示す。
まず、運動方程式をたてる。
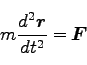 |
(198) |
であるが、動径方向の単位ベクトル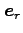 とそれと直交する単位ベクトル
とそれと直交する単位ベクトル
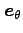 を基底する極座標で考える。惑星の速度ベクトルは
を基底する極座標で考える。惑星の速度ベクトルは
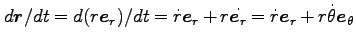 で表される。さらにそれを微分して、
で表される。さらにそれを微分して、
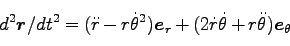 |
(199) |
よって、運動方程式を動径方向、角度方向に分解して書きくだすと、それぞれ、
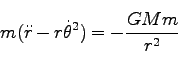 |
(200) |
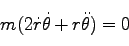 |
(201) |
となる。(194)を用いて、(201)は
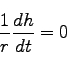 |
(202) |
と書ける。これはまさに角運動量保存則に他ならない。
また、(200)は、やはり(194)を用いて、
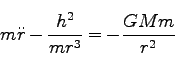 |
(203) |
とかける。
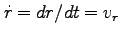 であることに注意して、上式を積分する。
であることに注意して、上式を積分する。
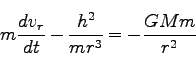 |
(204) |
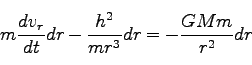 |
(205) |
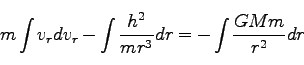 |
(206) |
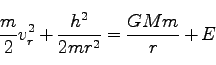 |
(207) |
 |
(208) |
ここで、積分定数を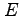 とした。
これは、エネルギー保存則に他ならない。
とした。
これは、エネルギー保存則に他ならない。
ここで(194)から、
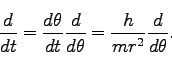 |
(209) |
よって、独立変数を時刻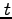 から
から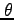 に変換して(207)は、
に変換して(207)は、
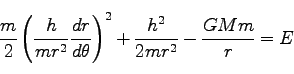 |
(210) |
と書ける。
この微分方程式が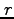 と
と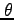 の関係を与えるので、
の関係を与えるので、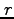 を
を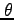 の関数として求めれば、惑星の軌道が求められたことになる。
ここで、
の関数として求めれば、惑星の軌道が求められたことになる。
ここで、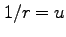 と変数を変換すると、以下のように変形できる。
と変数を変換すると、以下のように変形できる。
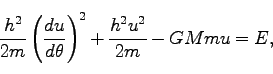 |
(211) |
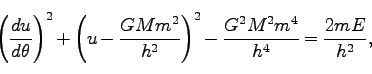 |
(212) |
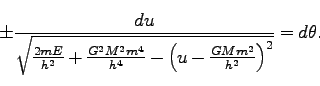 |
(213) |
ここで積分公式、
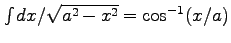 を用いて、
を用いて、
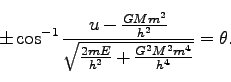 |
(214) |
よって、
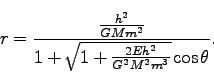 |
(215) |
ここで、
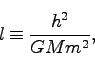 |
(216) |
 |
(217) |
と定義すれば、
(215)は、
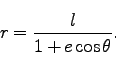 |
(218) |
と書ける。これは原点(太陽または地球)を焦点の一つとする円錐曲線の式で、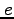 は離心率、
は離心率、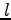 は半直弦と呼ばれる。
円錐曲線は、円錐を任意の断面で切ったときの断面の形で、楕円(
は半直弦と呼ばれる。
円錐曲線は、円錐を任意の断面で切ったときの断面の形で、楕円(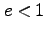 )、放物線(
)、放物線(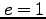 )、双曲線 (
)、双曲線 (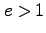 )、のいずれかである。
下図に、異なる離心率の円錐曲線の例を示す。
)、のいずれかである。
下図に、異なる離心率の円錐曲線の例を示す。
実際に太陽の周りの惑星(彗星)や地球の周りの人工衛星(探査機)の軌道も、楕円、放物線、双曲線のどれかである。
(217)より、離心率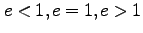 はそれぞれエネルギー
はそれぞれエネルギー 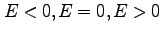 に対応している。すなわち、
全エネルギー
に対応している。すなわち、
全エネルギー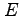 が負のときは、人工衛星は地球の重力に束縛されて、地球の周りを楕円軌道を描いて周回する(ケプラーの第一法則)。
運動エネルギーが増加するにつれ、離心率が大きくなり、やがて軌道は放物線となり、人工衛星は地球の重力圏を
脱出する。無限遠でエネルギーはゼロになる。さらに運動エネルギーが大きい場合は、双極線軌道になり、無限遠でも
正のエネルギーを持つ。
が負のときは、人工衛星は地球の重力に束縛されて、地球の周りを楕円軌道を描いて周回する(ケプラーの第一法則)。
運動エネルギーが増加するにつれ、離心率が大きくなり、やがて軌道は放物線となり、人工衛星は地球の重力圏を
脱出する。無限遠でエネルギーはゼロになる。さらに運動エネルギーが大きい場合は、双極線軌道になり、無限遠でも
正のエネルギーを持つ。




Next: 楕円軌道
Up: 二体問題
Previous: 換算質量
Contents
Ken EBISAWA
2011-05-30
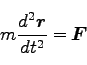
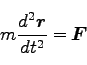
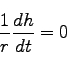
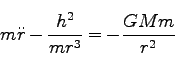
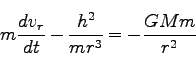
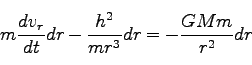
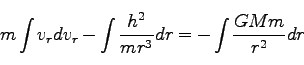

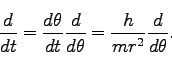
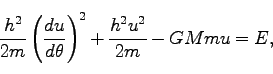
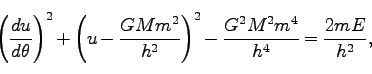
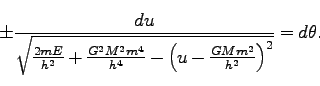
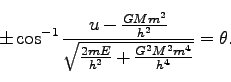
![]() はそれぞれエネルギー
はそれぞれエネルギー ![]() に対応している。すなわち、
全エネルギー
に対応している。すなわち、
全エネルギー![]() が負のときは、人工衛星は地球の重力に束縛されて、地球の周りを楕円軌道を描いて周回する(ケプラーの第一法則)。
運動エネルギーが増加するにつれ、離心率が大きくなり、やがて軌道は放物線となり、人工衛星は地球の重力圏を
脱出する。無限遠でエネルギーはゼロになる。さらに運動エネルギーが大きい場合は、双極線軌道になり、無限遠でも
正のエネルギーを持つ。
が負のときは、人工衛星は地球の重力に束縛されて、地球の周りを楕円軌道を描いて周回する(ケプラーの第一法則)。
運動エネルギーが増加するにつれ、離心率が大きくなり、やがて軌道は放物線となり、人工衛星は地球の重力圏を
脱出する。無限遠でエネルギーはゼロになる。さらに運動エネルギーが大きい場合は、双極線軌道になり、無限遠でも
正のエネルギーを持つ。