時刻![]() における質点の位置ベクトル
における質点の位置ベクトル![]() と、運動量
と、運動量![]() との外積
との外積
![]() を、原点Oに関する質点の、時刻
を、原点Oに関する質点の、時刻![]() における
角運動量と言う(以下、
における
角運動量と言う(以下、![]() で表す。)。
で表す。)。
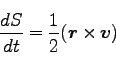 |
(191) |
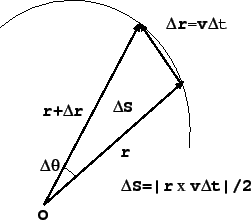
(190)式を微分し、運動方程式
![]() を用いると、
を用いると、
 |
(192) |
特に、力のモーメントがゼロの時、角運動量は一定に保たれる。これを角運動量保存則、あるいは面積速度保存則と言う。
力がゼロでなくても、それが働く方向が原点Oを通る場合(中心力)、![]() と
と![]() は平行なので、
は平行なので、
![]() 。
よって、質点が重力によって原点Oに引かれながら運動するとき、Oの周りの角運動量と面積速度は運動中一定に保たれる。
これから、「惑星と太陽を結ぶ動径は、単位時間に一定の面積を掃く」という
ケプラーの第二法則が導かれる。
。
よって、質点が重力によって原点Oに引かれながら運動するとき、Oの周りの角運動量と面積速度は運動中一定に保たれる。
これから、「惑星と太陽を結ぶ動径は、単位時間に一定の面積を掃く」という
ケプラーの第二法則が導かれる。
角運動量の大きさ![]() を
を![]() とする。速度ベクトル
とする。速度ベクトル![]() を
を![]() に平行な成分
に平行な成分![]() と垂直な成分
と垂直な成分![]() に分解すると、
下図からわかるように、
に分解すると、
下図からわかるように、
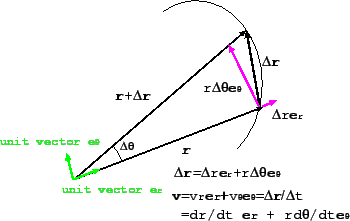
![]() だから、
だから、