二体問題の例

地球の公転:精密な天体観測を行う際、地球の公転運動を考慮に入れることが重要である。たとえば、パルサー(高速回転している中性子星)のタイミング観測を行うとき、地球がパルサーに近づいているか、遠ざかっているかで、見かけ上のパルス周期がドップラー効果に依って変化する。これを補正するために、地球の公転運動を精密に解き、天体からのパルスを解析するときには、そのパルス到達時刻 (pulse-arrival time)を、 太陽系重心 (barycenter)で測定した値に直す。これをbarycentric correctionと呼ぶ。

惑星の運動、人工衛星の運動:惑星と太陽の二体問題を解いて、惑星の軌道は、 第9.1節で説明する軌道六要素 を用いて記述される。 たとえば、「理科年表」を見ると、それらの軌道六要素が記述されている。 地球と人工衛星の二体問題を問いて、人工衛星の軌道も、軌道六要素で 記述される。地球大気による擾乱や、地球が扁平している効果によって、人工衛星の軌道はゆっくりと変化している。よって、軌道六要素を出す場合は、いつ測定した値であるかを明示する必要である。

惑星や人工衛星の位置を測定した時刻を元期(エポック、Epoch)と呼ぶ。エポックと軌道六要素が与えられらば、その前後の時刻 における惑星や人工衛星の位置は、解析的に求めることができる。人工衛星の 「軌道ファイル」には、六要素がエポックの関数として与えられている。

探査機: 地球の重力圏を脱出した探査機は、主に太陽の重力の影響を受け、太陽を焦点とするほぼ 楕円軌道を描き、 太陽系内を運動する。軌道を変えるために、地球や月によるスイングバイを利用する。その時の軌道は、地球や月を焦点とする双曲線、放物線になっている。

X線連星系: 太陽は連星系ではないが、多くの恒星は、連星系を成している。特に、通常の星とコンパクト星 (白色矮星、中性子星、ブラックホール)から成る連星系は、通常の星からコンパクト星に物質が落ちるときの 大きな重力エネルギーが開放されて、X線連星系となる。特にコンパクト星が回転している 中性子星の場合、これはX線パルサーとして観測され、公転運動によるドップラー効果の測定から、 視線方向の速度がわかり、二体問題を解くことによって、その軌道を正確に決めることができる。

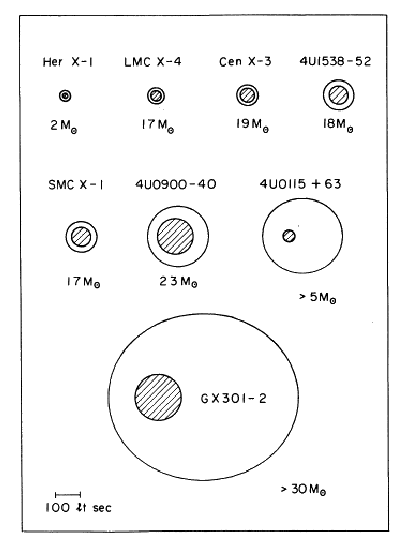
下図がX線連星パルサーの軌道の例である(Joss and Rappaport, 1984, Annual Review of Astronomy and Astrophysics, 22, 537より)。それぞれの天体名と、伴星の質量が書いてある。相対的な スケールは正しく示されている(左下の 線が100光秒)。中性子星の 質量はどれも大体$1.4 M_\odot$。4U0115+63($e=0.34$)やGX301-2($e=0.47$)は 離心率の大きい楕円軌道であるが、離心率もドップラー効果の観測から測定できることに注意。

重力波の間接的検証:

電荷を持った物体が加速度運動すると電磁波を放出するように、質量を持った物体が運動すると 重力波 が放出される、と一般相対論は予言している。重力波はあまりにも弱いので、今だ直接検出されていないが、 連星パルサーの観測から、間接的に重力波の存在が検証されている。 ハルスとテイラーは、PSR 1913+16という連星パルサーを、プエルトリコにある電波望遠鏡を用い、1974年 の発見以来、長期間モニター観測を行った。その結果、その軌道がほんの少しずつ変化していることが わかった。これはニュートン力学では説明できない。一方、一般相対論によると、重力波の放射によって、 連星パルサーはエネルギーを失ない、それによって、徐々に軌道が変化していく。その計算結果 と観測された軌道変化がピタリと一致した。これが、今日では(唯一)の重力波の観測的証拠だと 考えられている。ハルスとテイラーは、この業績により、1993年のノーベル物理学賞を 受賞した。