天体が原点Oの重力に引かれて運動するときは、Oの周りの角運動量が保存するので、その問題は簡単になる。 しかし、一般に二つの天体が重力で引きあっているときには、両方の運動を考えなくてはいけないので、問題は複雑になるのではないだろうか? その心配がないことを以下で述べる。
例として、惑星(質量![]() )が太陽(質量
)が太陽(質量![]() )のまわりを公転運動する場合を考えよう。それぞれの位置ベクトルを
)のまわりを公転運動する場合を考えよう。それぞれの位置ベクトルを
![]() とすれば、
とすれば、
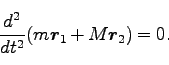 |
(196) |
一方、(195)から次式も導ける。
これは、太陽に対する惑星の位置(
![]() に、換算質量
に、換算質量
![]() の天体がある場合の運動を表わす運動方程式である。
の天体がある場合の運動を表わす運動方程式である。
一般に二つの質点が互いに力を及ぼしあって運動するとき、個々の質点の運動方程式を、質量中心の運動方程式と、 一方の質点が静止しているかのようにみなしたときの他方の質点の運動方程式(ただし、質量が換算質量にかわっている)に書き換えることができる。 二体問題(195)を解くかわりに、それと等価な一体問題(197)を解けば良いことになる。