



Next: ケプラーの第三法則
Up: 二体問題
Previous: 人工衛星の軌道、惑星の軌道
Contents
楕円は、二つの焦点からの距離の和が等しい点をつなげたものである。下図のように長半径を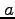 、短半径を
、短半径を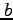 とする。
楕円の面積は
とする。
楕円の面積は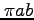 で与えられる。
で与えられる。
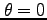 の点がA,
の点がA,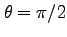 の点がQ,
の点がQ, の点がCである。
右側の焦点、
の点がCである。
右側の焦点、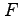 からの距離を考える。Aが近日点、Cが遠日点である。
からの距離を考える。Aが近日点、Cが遠日点である。
下図と(218)より、
 。よって、
。よって、
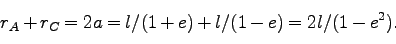 |
(219) |
これから、長半径は
 |
(220) |
と書けることがわかる。よって、
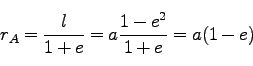 |
(221) |
だから、下図に書いてあるとおり
 である。
である。
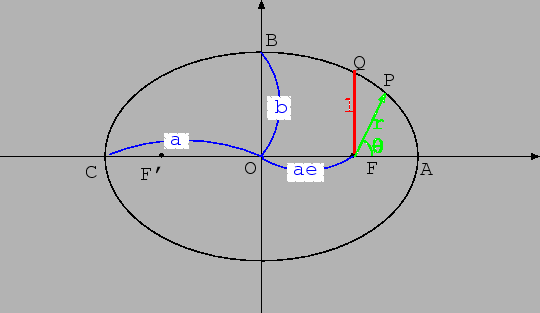
次に短半径を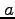 と
と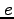 で表わす。楕円の定義より、
で表わす。楕円の定義より、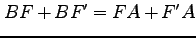 である。
である。
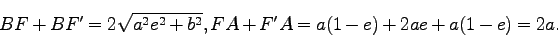 |
(222) |
よって、
 |
(223) |
ここで、(220)を使った。
(216),(217)と(220)より、
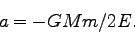 |
(224) |
つまり、
軌道長半径は、エネルギー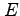 だけで決まる。
同様に、(223)と(216)を使って、
だけで決まる。
同様に、(223)と(216)を使って、
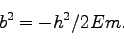 |
(225) |
これら二つの式は、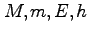 が与えられらば、一意的に
が与えられらば、一意的に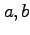 、つまり楕円軌道が決まることを表わしている。
、つまり楕円軌道が決まることを表わしている。
Ken EBISAWA
2011-05-30
![]() 、短半径を
、短半径を![]() とする。
楕円の面積は
とする。
楕円の面積は![]() で与えられる。
で与えられる。
![]() の点がA,
の点がA,![]() の点がQ,
の点がQ,![]() の点がCである。
右側の焦点、
の点がCである。
右側の焦点、![]() からの距離を考える。Aが近日点、Cが遠日点である。
からの距離を考える。Aが近日点、Cが遠日点である。
![]() 。よって、
。よって、
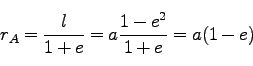
![]() と
と![]() で表わす。楕円の定義より、
で表わす。楕円の定義より、![]() である。
である。