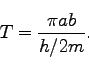


Next: 円軌道の場合
Up: 二体問題
Previous: 楕円軌道
Contents
楕円の長半径を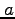 、短半径を
、短半径を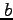 としたとき、その面積は
としたとき、その面積は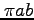 で与えられる。角運動量を
で与えられる。角運動量を
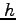 、天体の質量を
、天体の質量を とするとすると、面積速度は
とするとすると、面積速度は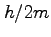 である。よって、天体の公転周期
である。よって、天体の公転周期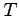 は、
は、
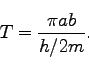 |
(226) |
である。ここで、(223)と(216)を使って、
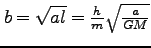 だから、
だから、
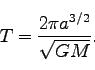 |
(227) |
これが、「惑星の公転周期の二乗が軌道長半径の三乗に比例する」、というケプラーの第三法則
である。
Ken EBISAWA
2011-02-08
![]() 、短半径を
、短半径を![]() としたとき、その面積は
としたとき、その面積は![]() で与えられる。角運動量を
で与えられる。角運動量を
![]() 、天体の質量を
、天体の質量を![]() とするとすると、面積速度は
とするとすると、面積速度は![]() である。よって、天体の公転周期
である。よって、天体の公転周期![]() は、
は、