ドップラー効果と光行差 (aberration)

電磁波の伝播を考えるとき、電磁波の波数ベクトルを${\bf k}$ ( $\vert{\bf k}\vert=\omega/c$)、 角振動数を$\omega$として、

$$({\bf k}, i\omega/c)$$ (103)

は四元ベクトルである。その長さは、

$${\bf k}\cdot {\bf k} - \omega^2/c^2 =0$$ (104)

となり、ローレンツ不変量であることがわかる。また、四元ベクトル、

$$(x, y, z, ict)$$ (105)

との内積をとると、

$${\bf k}\cdot {\bf x} - \omega t$$ (106)

は、電磁波の位相を与え、これもローレンツ不変量である。

$K$系と、その$z$方向に速度$v$で走る$K'$系の間の ローレンツ変換の式(72)と、四元速度の定義(89)から、

$$\left(\begin{array}{c} k'_x \\ k'_y \\ k'_z \\ \omega' i/... ...{c} k_x \\ k_y \\ k_z \\ \omega i/c \\ \end{array}\right).$$ (107)

波数の定義から $\vert{\bf k}\vert=\omega/c$、 $\vert{\bf k'}\vert=\omega'/c$で、 ベクトル${\bf k}$がyz平面にあり、 電磁波が進む向きと $z$軸、$z'$軸のなす角を $\theta, \theta'$とすると、 $k_y=(\omega/c) \sin \theta$、 $k'_y=(\omega'/c) \sin \theta'$ $k_z=(\omega/c) \cos \theta$、 $k'_z=(\omega'/c) \cos \theta'$ である。よって、(107)を書きくだすと、

$$\omega'\; \sin \theta' =\omega\; \sin \theta$$ (108)

$$\omega'\; \cos \theta' =\omega \: \gamma (\cos \theta - \beta)$$ (109)

$$\omega' = \omega\; \gamma \; (1 - \beta \cos \theta) = \frac{\omega}{\sqrt{1-(v/c)^2}}\left(1-\frac{v}{c}\cos\theta\right)$$ (110)

となる。式(108)と(109)の比を取ると、

$$\tan \theta' =\frac{\sin \theta}{\gamma(\cos \theta - \beta)} =\frac{\sqrt{1 - (v/c)^2} \sin \theta}{\cos \theta - v/c}$$ (111)

が得られる。

式(110)は、光のドップラー効果に他ならない。$v\ll c$のとき、 $(v/c)^2$の項を無視すれば、これは

$$\omega' = \omega \;\left(1-\frac{v}{c}\cos\theta\right)$$ (112)

となり、音波の場合と同じように、非相対論的なドップラー効果を表す。$(v/c)^2$の項を無視できないとき、 式(110)で、$\theta=0$、光源が視線方向と垂直に運動しているときにも 波長が変化することに注意。これを横ドップラー効果と呼ぶ。

式(111)は、地球の公転運動によって、星からの光の到来方向が変化する 光行差 (aberration)を説明する。地球の公転速度は、$v \approx 30$ km/s, $v/c \approx 10^{-4}$である。地球の公転面と垂直方向から星の光がやってくるとき、 $\theta= 90^\circ$なので、

$$\tan \theta' = - \frac{c}{v} \sqrt{1 - (v/c)^2}$$ (113)

である。

$\tan (\theta' -\pi/2) = - 1 /\tan \theta'$を使って、 $\theta' -\pi/2=\alpha$とすると(下図参照)

$$\tan \alpha = \frac{v}{c}\frac{1}{\sqrt{1 - (v/c)^2}}.$$ (114)

非相対論的には、単純にベクトルの大きさから、

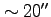$$\tan \alpha = \frac{v}{c}$$ (115)

が得られるが、これは式(114)で、 $(v/c)^2$の項を無視した場合と一致する。

$v/c \approx 10^{-4}$は、角度では$\sim20''$に対応する。地球の公転のために、季節 (地球の公転運動の方向の違い)によって、星の見かけの位置は最大$\pm20''$変化する。 $(v/c)^2\approx10^{-8}$は、角度では$\sim2$ marcsec (ミリ秒角)に対応していて、 それほど高分解能の観測は電波干渉計によって可能であるが、それ以外のほとんどの天文観測においては 装置の位置分解能以下なので、 無視しても構わない。