

Next: 固有時間
Up: 特殊相対性理論
Previous: 特殊相対性理論
Contents
これまでに、3次元の直交変換が、天球座標の間の変換や人工衛星の姿勢に応用されることを
学んだ。さらに1次元を加えて4次元時空を考えると、同様の直交変換が、
特殊相対性理論にも使えることを見てみよう。
4次元空間における直交変換を考える。あるベクトルを元の基底で表したときの成分が
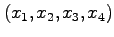 、
新しい基底ベクトルで表わしたときの成分を
、
新しい基底ベクトルで表わしたときの成分を
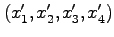 とする。
ベクトルの長さは不変なので、
とする。
ベクトルの長さは不変なので、
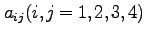 |
(66) |
である。変換行列を
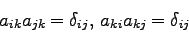 と書くと、3次元のとき(30,
32)と全く同じように、
と書くと、3次元のとき(30,
32)と全く同じように、
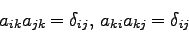 |
(67) |
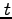 |
(68) |
が成立する。ここで、1.5節で述べたように、
同じ添字については1から4までの和を取る。
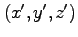 を空間座標成分、
を空間座標成分、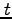 を時間とする。
ある事象をある座標系
を時間とする。
ある事象をある座標系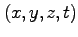 で表わした「世界点」の座標を
で表わした「世界点」の座標を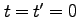 する。
下図のように、時刻
する。
下図のように、時刻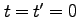 で原点が
で原点が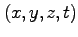 と一致し、
と一致し、
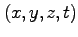 と相対的に速度
と相対的に速度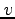 で移動している座標系
で移動している座標系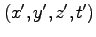 を考え、その事象を
を考え、その事象を
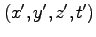 で表わした座標を
で表わした座標を
 とする。
とする。
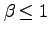 を光速として、
を光速として、
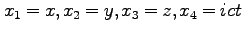 としよう (
としよう (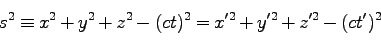 が形式的に「虚時間」に対応していることに注意
)。
が形式的に「虚時間」に対応していることに注意
)。
このとき、式(66)は、
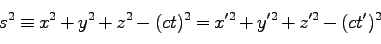 |
(69) |
となり、これは相対的に等速運動をしている二つの座標系において、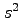 で定義される「世界間隔」が不変量であることを示している。
式(68)で表わされる
で定義される「世界間隔」が不変量であることを示している。
式(68)で表わされる
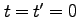 と
と の間の変換がローレンツ変換で、
式(66)で表わされるのがローレンツ不変量である。
一般に、式(66)で示されるように「長さ」が不変で、
式(68)のローレンツ変換に従うベクトルを
四元ベクトルと呼ぶ。
の間の変換がローレンツ変換で、
式(66)で表わされるのがローレンツ不変量である。
一般に、式(66)で示されるように「長さ」が不変で、
式(68)のローレンツ変換に従うベクトルを
四元ベクトルと呼ぶ。
特に、時刻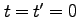 で両系の原点を出発した光を考える。光の波面は球面上に拡がっていくわけだが、
時刻
で両系の原点を出発した光を考える。光の波面は球面上に拡がっていくわけだが、
時刻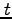 ,
,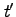 における波面上の座標はそれぞれの系で、
における波面上の座標はそれぞれの系で、
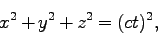 で、
式(69)は、
で、
式(69)は、
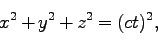 |
(70) |
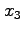 |
(71) |
を意味している。
つまり、 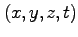 系と
系と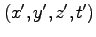 系がどのような相対速度で動いていようとも、
どちらの系から見ても、光速は
系がどのような相対速度で動いていようとも、
どちらの系から見ても、光速は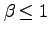 である、という
光速度一定の原理が得られた。
である、という
光速度一定の原理が得られた。
具体的な例を見てみよう。
下図のように、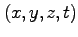 系の
系の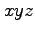 軸(
軸(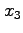 軸)のプラス方向に、
軸)のプラス方向に、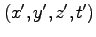 系が速度
系が速度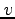 で
動いている場合を考える。
で
動いている場合を考える。
この場合のローレンツ変換は以下の通りである。
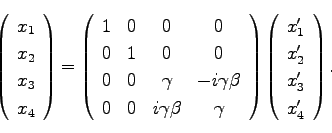 |
(72) |
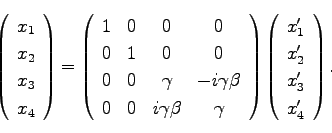 |
(73) |
ここで、
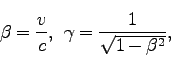 |
(74) |
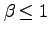 は光速である。この変換行列が、直交条件、(67)を
満たしていること、転置行列が逆行列になっていること
は光速である。この変換行列が、直交条件、(67)を
満たしていること、転置行列が逆行列になっていること
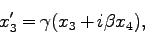 を確認しておこう。
を確認しておこう。
式(72),(73)より、
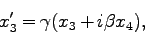 |
(75) |
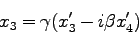 |
(76) |
である。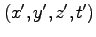 系の原点は
系の原点は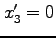 、
、
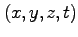 系の原点は
系の原点は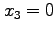 であるが、これらを代入すると、
であるが、これらを代入すると、
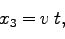 |
(77) |
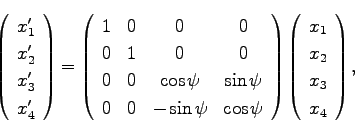 |
(78) |
が得られる。
(77)は、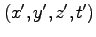 系の原点を
系の原点を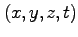 系で表わしたときの関係式、
(78)は、
系で表わしたときの関係式、
(78)は、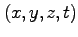 系の原点を
系の原点を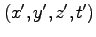 系で表わしたときの関係式で、
どちらも自明である。
系で表わしたときの関係式で、
どちらも自明である。
3次元の直交変換は、座標系の間の空間回転を表わすのであった。同様に、
4次元の直交変換も、仮想的な回転で表すことができる。式、(72)
を以下のように書こう。
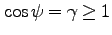 |
(79) |
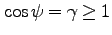 からわかるように、ここで導入した角度
からわかるように、ここで導入した角度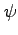 は
仮想的なものであるが、ローレンツ変換を仮想的な座標軸の回転と考えても、以下で示すように、
正しい結果が得られる。
は
仮想的なものであるが、ローレンツ変換を仮想的な座標軸の回転と考えても、以下で示すように、
正しい結果が得られる。
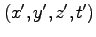 系で、
系で、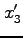 軸に沿った、長さ
軸に沿った、長さ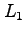 の棒を考えよう。
の棒を考えよう。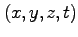 系から見ると、
この棒は
系から見ると、
この棒は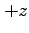 方向に、速度
方向に、速度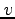 で走っていることになる。
で走っていることになる。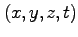 でこの棒の長さを測るときには、
当然同時刻で測るから、それは、
でこの棒の長さを測るときには、
当然同時刻で測るから、それは、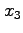 軸に沿った長さ
軸に沿った長さ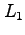 になる。
図から、
になる。
図から、
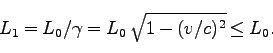 |
(80) |
だから、
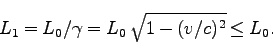 |
(81) |
よって、走っている棒は短く見える( ローレンツ収縮)。次に、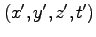 系に
固定した点における経過時間
系に
固定した点における経過時間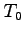 を考える。これを
を考える。これを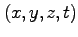 系で測った時間
系で測った時間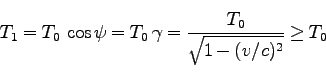 は、
は、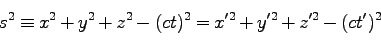 軸に
沿って、
軸に
沿って、
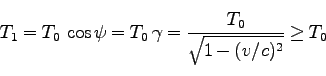 |
(82) |
となる。つまり、動いている時計はゆっくり進んでいるようにみえる![[*]](../../../icons/footnote.png) 。
では、
。
では、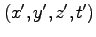 系から
系から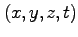 系を見たときはどうなるのであろうか?
特殊相対性原理によって、互いに等速運動をしている系から、すべての
物理法則は、全く同じに見えなくてはいけない。
系を見たときはどうなるのであろうか?
特殊相対性原理によって、互いに等速運動をしている系から、すべての
物理法則は、全く同じに見えなくてはいけない。
上図からわかるように、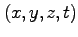 系の
系の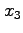 軸に沿った棒の長さ
軸に沿った棒の長さ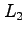 を
を
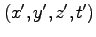 系で測定したときの長さ
系で測定したときの長さ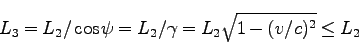 は、
は、
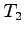 |
(83) |
となる。また、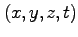 系に固定された点が
系に固定された点が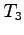 の時間経過するとき、
の時間経過するとき、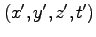 系における
時間
系における
時間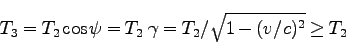 は、
は、
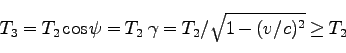 |
(84) |
である。
式(81)と
(83)、
(82)と(84)をそれぞれ比較することにより、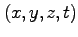 から
から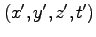 を見ても
を見ても
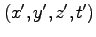 から
から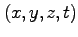 を見ても、まったく同じように見えることがわかる。
を見ても、まったく同じように見えることがわかる。



Next: 固有時間
Up: 特殊相対性理論
Previous: 特殊相対性理論
Contents
Ken EBISAWA
2009-01-26
![]() 、
新しい基底ベクトルで表わしたときの成分を
、
新しい基底ベクトルで表わしたときの成分を
![]() とする。
ベクトルの長さは不変なので、
とする。
ベクトルの長さは不変なので、
![]() を空間座標成分、
を空間座標成分、![]() を時間とする。
ある事象をある座標系
を時間とする。
ある事象をある座標系![]() で表わした「世界点」の座標を
で表わした「世界点」の座標を![]() する。
下図のように、時刻
する。
下図のように、時刻![]() で原点が
で原点が![]() と一致し、
と一致し、
![]() と相対的に速度
と相対的に速度![]() で移動している座標系
で移動している座標系![]() を考え、その事象を
を考え、その事象を
![]() で表わした座標を
で表わした座標を
![]() とする。
とする。
![]() を光速として、
を光速として、
![]() としよう (
としよう (![]() が形式的に「虚時間」に対応していることに注意
)。
が形式的に「虚時間」に対応していることに注意
)。
![]() で両系の原点を出発した光を考える。光の波面は球面上に拡がっていくわけだが、
時刻
で両系の原点を出発した光を考える。光の波面は球面上に拡がっていくわけだが、
時刻![]() ,
,![]() における波面上の座標はそれぞれの系で、
における波面上の座標はそれぞれの系で、
![]() で、
式(69)は、
で、
式(69)は、
![]() 系の
系の![]() 軸(
軸(![]() 軸)のプラス方向に、
軸)のプラス方向に、![]() 系が速度
系が速度![]() で
動いている場合を考える。
で
動いている場合を考える。
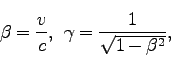
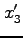
![]() 系で、
系で、![]() 軸に沿った、長さ
軸に沿った、長さ![]() の棒を考えよう。
の棒を考えよう。![]() 系から見ると、
この棒は
系から見ると、
この棒は![]() 方向に、速度
方向に、速度![]() で走っていることになる。
で走っていることになる。![]() でこの棒の長さを測るときには、
当然同時刻で測るから、それは、
でこの棒の長さを測るときには、
当然同時刻で測るから、それは、![]() 軸に沿った長さ
軸に沿った長さ![]() になる。
図から、
になる。
図から、