


Next: ドップラー効果と光行差 (aberration)
Up: 特殊相対性理論
Previous: 速度の変換則
Contents
四元速度に質量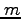 を書けたものを四元運動量と呼ぶ。
すなわち、
を書けたものを四元運動量と呼ぶ。
すなわち、
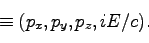 |
(96) |
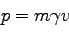 |
(97) |
ここで、相対論的には運動量は
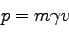 |
(98) |
で、
エネルギーは、
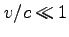 |
(99) |
で表されることを用いた。
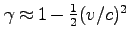 のとき、
のとき、
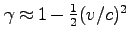 を用いて、
(99)は、
を用いて、
(99)は、
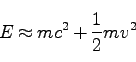 |
(100) |
と近似できる。最初の項が静止エネルギー、二番目の項が、ニュートン力学における
通常の運動エネルギーである。
(90)より、四元運動量の長さの二乗は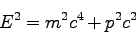 だから、
良く知られたエネルギーと運動量の間の関係式、
だから、
良く知られたエネルギーと運動量の間の関係式、
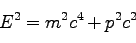 |
(101) |
が得られる。
特に、光子など質量がゼロである素粒子の場合は、
 |
(102) |
光の波長を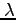 ,振動数を
,振動数を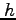 とするとき、
とするとき、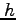 をプランク定数として、光子のエネルギーは
をプランク定数として、光子のエネルギーは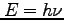 ,運動量は
,運動量は
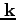 で表わされることを思いだそう。
あたりまえだが、光子について、(101)が成立している。
で表わされることを思いだそう。
あたりまえだが、光子について、(101)が成立している。
Ken EBISAWA
2009-01-26
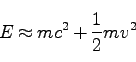
![]() だから、
良く知られたエネルギーと運動量の間の関係式、
だから、
良く知られたエネルギーと運動量の間の関係式、