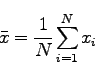 |
(244) |
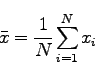 |
(244) |
計算してみると、
![]() となる。
ここで、
となる。
ここで、![]() 分布の表(図19)と照らし合わせる
分布の表(図19)と照らし合わせる![]() 。
表には自由度99はないが、それほど変わらないので、自由度100の
。
表には自由度99はないが、それほど変わらないので、自由度100の![]() 分布を見てみる。
ここには、「上側確率」の値と、それを与える
分布を見てみる。
ここには、「上側確率」の値と、それを与える![]() の値が書いてある。
たとえば、上側確率が0.5, 0.1, 0.01, 0.001となる
の値が書いてある。
たとえば、上側確率が0.5, 0.1, 0.01, 0.001となる![]() の値は、それぞれ
0.993, 1.358, 1.494である。これは、自由度100の
の値は、それぞれ
0.993, 1.358, 1.494である。これは、自由度100の![]() 分布において、
分布において、
![]() が1.494以上であるような事象の起きる確率は0.001以下(非常に稀)であることを意味している。
それにたいして、現在の
が1.494以上であるような事象の起きる確率は0.001以下(非常に稀)であることを意味している。
それにたいして、現在の
![]() という値は、「なんてことのない」値で、
自由度100の
という値は、「なんてことのない」値で、
自由度100の![]() 分布において普通に起こりうる。よって、
図13のライトカーブ、図14のヒストグラムで与えられる天体の時間変動は一定だと
考えてよい。
分布において普通に起こりうる。よって、
図13のライトカーブ、図14のヒストグラムで与えられる天体の時間変動は一定だと
考えてよい。
 |
では、図20で与えられるライトカーブの場合はどうであろうか?これは
先のライトカーブで、一ビンだけ、カウント数を15から65に作為的に変更したものである。
もし、このようなライトカーブが観測されたとしたら、これは統計的なゆらぎで起きうることだろうか?
あるいは、「X線フラッシュ」![]() のような宇宙現象であろうか?先の例と同様に、平均を計算すると25.58となる。
のような宇宙現象であろうか?先の例と同様に、平均を計算すると25.58となる。![]() ,
,
![]() である。
である。![]() 分布の表と照らし合わせると、このように大きな
分布の表と照らし合わせると、このように大きな
![]() の値が起きる確率は、0.01以下であるが、0.001以上であることがわかる。ライトカーブ
から作った
の値が起きる確率は、0.01以下であるが、0.001以上であることがわかる。ライトカーブ
から作った![]() が、もし
が、もし![]() 分布に従うとしたら非常に稀なことが起きた、ということは、
そもそもそれが
分布に従うとしたら非常に稀なことが起きた、ということは、
そもそもそれが![]() 分布に従っていないこと、つまり各ビンに落ちてくるX線光子数の分布は、ある
平均値の回りの正規分布にしたがっていない(=この天体は時間変動している)ことを示唆する。
分布に従っていないこと、つまり各ビンに落ちてくるX線光子数の分布は、ある
平均値の回りの正規分布にしたがっていない(=この天体は時間変動している)ことを示唆する。
まとめると、図20のようなX線天体の時間変動が観測されたとき、この天体の強度が 一定であると言う仮説は、危険率0.01で棄却できる(これほど稀な事は、偶然には100回に一回も起こらない)。しかし、危険率0.001では棄却できない(これほど珍しい事でも、1000回に一回は偶然起きることがある)。