



Next: カイ二乗検定
Up: 統計入門
Previous: 標準偏差と偏差値
Contents
平均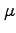 , 標準偏差
, 標準偏差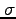 である正規分布に従う確率変数
である正規分布に従う確率変数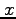 を、えいやっ、と取ってきて
を、えいやっ、と取ってきて
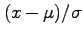 という量を作ってみよう。これは、0の回りに対称にばらつき、大きく0からずれることは稀なので、
-1から+1の間の値を取る事が多いだろう。
という量を作ってみよう。これは、0の回りに対称にばらつき、大きく0からずれることは稀なので、
-1から+1の間の値を取る事が多いだろう。
では、同じ正規分布を考え、そこから
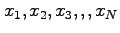 という
という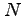 個の値をとってきて、
個の値をとってきて、
 |
(243) |
という量を定義したら、その値はどうなるだろうか?
各項は1の回りにばらついているので、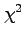 は
は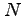 の回りにばらつくはずである。
の回りにばらつくはずである。
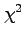 の従う確率分布を自由度
の従う確率分布を自由度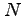 の
の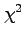 分布(カイ二乗分布)と呼ぶが、その平均は
上記の推測通り
分布(カイ二乗分布)と呼ぶが、その平均は
上記の推測通り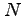 である。また、その分散は
である。また、その分散は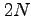 であることがわかっている。
であることがわかっている。
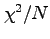 のことをreduced
のことをreduced 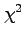 (
(
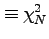 ) と呼び、この値は1に近い。
) と呼び、この値は1に近い。
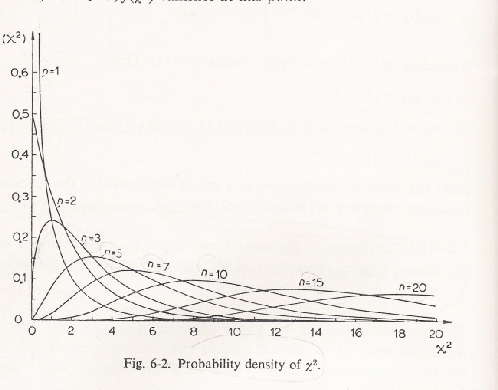
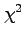 分布の表式はやや複雑なので、ここには記さないが、それをプロットしたものは
図18の通りである。それぞれ、自由度が平均に
なっていること、(当然であるが)積分すると1になっていることに注意。
分布の表式はやや複雑なので、ここには記さないが、それをプロットしたものは
図18の通りである。それぞれ、自由度が平均に
なっていること、(当然であるが)積分すると1になっていることに注意。
Figure:
自由度1, 2, 3, 5, 7, 10, 15, 20の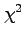 分布。''Statistical and Computation
Methods in Data Analysis''(ISBN 0-7204-0334-0)より。
分布。''Statistical and Computation
Methods in Data Analysis''(ISBN 0-7204-0334-0)より。
 |
Ken EBISAWA
2011-05-30
![]() という
という![]() 個の値をとってきて、
個の値をとってきて、
