



Next: (カイ二乗)分布
Up: 統計入門
Previous: 正規分布
Contents
分散、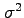 の平方根、
の平方根、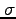 が標準偏差である。これは、確率分布が
どれだけ平均の回りに集中しているかを示す量である。同じ平均
が標準偏差である。これは、確率分布が
どれだけ平均の回りに集中しているかを示す量である。同じ平均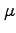 を持つ正規分布でも、
を持つ正規分布でも、
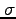 が小さい分布は「細く」、
が小さい分布は「細く」、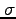 が大きい分布は「太い」ことがわかるだろう(図16)。
いつでも確率分布を
が大きい分布は「太い」ことがわかるだろう(図16)。
いつでも確率分布を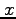 で積分すると1になることに注意。
で積分すると1になることに注意。
Figure:
平均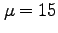 , 標準偏差
, 標準偏差
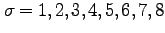 の正規分布の比較。
の正規分布の比較。
|
正規分布を、横軸を平均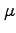 からのずれを
からのずれを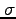 を単位にして描いてみよう(図17)。
この図は、正規分布において、確率変数の平均からのずれが
を単位にして描いてみよう(図17)。
この図は、正規分布において、確率変数の平均からのずれが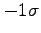 から
から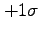 のあいだにある
確率は68.26 %、というように見る。同様に、平均からのずれが
のあいだにある
確率は68.26 %、というように見る。同様に、平均からのずれが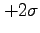 よりも大きい確率は、約2.27 %であることがわかる。
よりも大きい確率は、約2.27 %であることがわかる。
Figure:
正規分布において、横軸を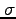 を単位として表したときの確率分布
を単位として表したときの確率分布
|
ある確率変数が、どれだけ平均からずれているかを表すときに、「何々シグマ」という言い方をする。
たとえば、仮に日本人男性の身長の分布が165cmで、標準偏差が8cmの正規分布に従うとすると、
身長181cmの人は平均よりも2シグマ背が高く、それよりも背が高い人は、人口の中の約2.27 %である。
身長189cmの人は平均よりも3シグマ背が高く、それよりも背が高い人は、人口の中の約0.13 %である。
いわゆる「偏差値」は、平均を50, 1シグマを10としたときに、平均からどれだけずれているかを
示す指標である。たとえば、偏差値70というのは平均よりも2シグマ上位にいることで、それよりも
上位の人は全体の約2.27 %である。
Ken EBISAWA
2011-05-30