



Next: 四元速度
Up: 特殊相対性理論
Previous: ローレンツ変換
Contents
式(117)で示されるように、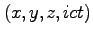 の長さは
ローレンツ不変量であるから、微少なベクトル
の長さは
ローレンツ不変量であるから、微少なベクトル
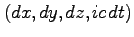 の長さもローレンツ不変
である。すなわち、
の長さもローレンツ不変
である。すなわち、
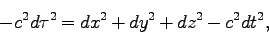 |
(133) |
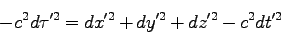 |
(134) |
と書いたとき、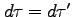 である
である![[*]](file:/usr/local/share/lib/latex2html/icons/footnote.png) 。
。
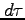 は、
は、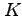 系の時計で
系の時計で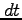 の間に
の間に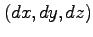 移動する物体とともに動く
(
移動する物体とともに動く
(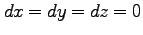 )観測者の測る時間、
)観測者の測る時間、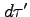 は、
は、
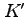 系の時計で、
系の時計で、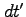 の間に
の間に
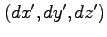 移動する物体とともに動く(
移動する物体とともに動く(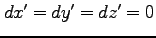 )観測者の測る時間である。つまり、物体とともに動く時計で測った時間は不変量であり
)観測者の測る時間である。つまり、物体とともに動く時計で測った時間は不変量であり![[*]](file:/usr/local/share/lib/latex2html/icons/footnote.png) 、この
、この
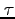 を固有時間と呼ぶ。
を固有時間と呼ぶ。
式(133)を、
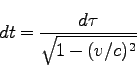 |
(135) |
と書くと、
これはまさに式(130)と同値で、
動いている時計はゆっくり進んでいるように見えることを示している。
Ken EBISAWA
2011-05-30