


Next: 静止衛星
Up: 人工衛星の軌道
Previous: 人工衛星の軌道
Contents
軌道六要素
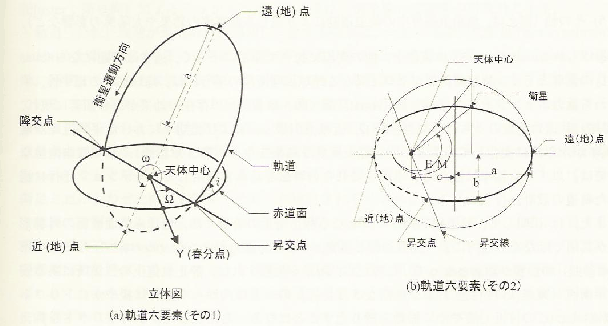
ある時刻(エポック)における人工衛星の軌道(一般に楕円軌道)と位置は、以下で示す軌道六要素を用いて記述できる。
図7は「人工衛星の力学と制御ハンドブック」より![[*]](../../../icons/footnote.png) 。
。
Figure:
人工衛星の軌道を記述する軌道六要素。「人工衛星の力学と制御ハンドブック」
 |
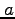 :軌道長半径 (semi-major axis)。円軌道のときは、円の半径。
:軌道長半径 (semi-major axis)。円軌道のときは、円の半径。
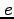 :離心率 (eccentricity)
:離心率 (eccentricity) 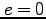 は円軌道。
は円軌道。
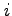 :軌道傾斜角 (inclination)。地球の赤道面と人工衛星の軌道面がなす角度。
:軌道傾斜角 (inclination)。地球の赤道面と人工衛星の軌道面がなす角度。
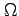 :昇交点赤経 (right ascension of the ascending node)。
:昇交点赤経 (right ascension of the ascending node)。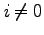 のとき、地球の赤道面と人工衛星の軌道面が交差する点の赤経。
のとき、地球の赤道面と人工衛星の軌道面が交差する点の赤経。
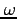 :近地点引数 (argument of perigee)。楕円軌道の場合、昇交点から測って近地点が軌道面上のどこに来るかを表わす。
:近地点引数 (argument of perigee)。楕円軌道の場合、昇交点から測って近地点が軌道面上のどこに来るかを表わす。
以上5つのパラメーターで軌道は決まる。
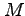 :平均近点離角 (mean anomaly)。与えられたエポックにおける人工衛星の軌道上での位置を表す。
:平均近点離角 (mean anomaly)。与えられたエポックにおける人工衛星の軌道上での位置を表す。
図8に、1987年2月5日に打ちあげられ、1991年11月1日に大気圏に再突入した
「ぎんが」衛星の軌道六要素の時間変化を示す。
Figure:
ぎんが衛星の軌道六要素の打ち上げから大気圏再突入までの時間変化。
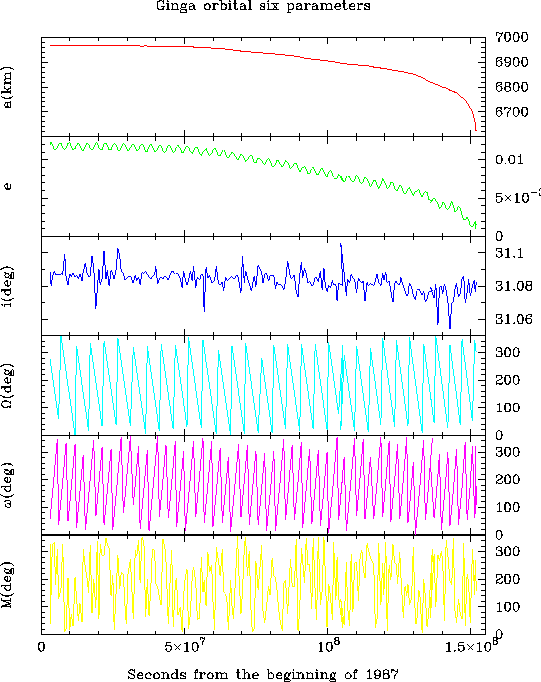 |
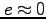 から、ほぼ円軌道であることがわかる。
地球の半径は、約6378kmだから、ぎんが衛星の打ち上げ時の高度は、約550 km。軌道傾斜角
から、ほぼ円軌道であることがわかる。
地球の半径は、約6378kmだから、ぎんが衛星の打ち上げ時の高度は、約550 km。軌道傾斜角
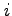 が、「ぎんが」衛星が打ち上げられた内之浦宇宙空間観測所の緯度に対応していることに注意しよう。地球の自転速度を稼ぐために、人工衛星は真東に打たれる。
その結果、軌道傾斜角が打ち上げ地の緯度に一致することになる。
が、「ぎんが」衛星が打ち上げられた内之浦宇宙空間観測所の緯度に対応していることに注意しよう。地球の自転速度を稼ぐために、人工衛星は真東に打たれる。
その結果、軌道傾斜角が打ち上げ地の緯度に一致することになる。
もし衛星の軌道の地球に対する相対的な位置が不変ならば、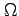 も
も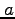 ,
, 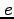 ,
, 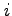 と同じくほぼ一定のはずであるが、
と同じくほぼ一定のはずであるが、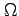 は周期的に
変化している。これは、地球が扁平である影響で人工衛星の軌道面が歳差運動をしているためである。
ほぼ円軌道なので、近地点の位置を表わす
は周期的に
変化している。これは、地球が扁平である影響で人工衛星の軌道面が歳差運動をしているためである。
ほぼ円軌道なので、近地点の位置を表わす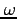 はあまり意味を持たない。
はあまり意味を持たない。
ミッションの終了近くになって、大気の摩擦のために、急激に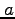 が減少(衛星が降下)していることがわかる。
また、もともと離心率は小さくほぼ円軌道であったが、衛星が降下するにつれて、さらに
円軌道からのずれが「なまされて」、離心率も減少していることがわかる。
が減少(衛星が降下)していることがわかる。
また、もともと離心率は小さくほぼ円軌道であったが、衛星が降下するにつれて、さらに
円軌道からのずれが「なまされて」、離心率も減少していることがわかる。
式(227)より、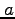 から衛星の公転周期が求められる。
地球のシュワルツシルド半径、
から衛星の公転周期が求められる。
地球のシュワルツシルド半径、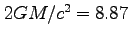 mmを使うと、以下のように簡単に計算できる。
mmを使うと、以下のように簡単に計算できる。
このようにして求められた公転周期と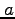 の関係を図9に示す。
の関係を図9に示す。
Figure:
ぎんが衛星の打ち上げから大気圏再突入までの軌道長半径と周期の変化。
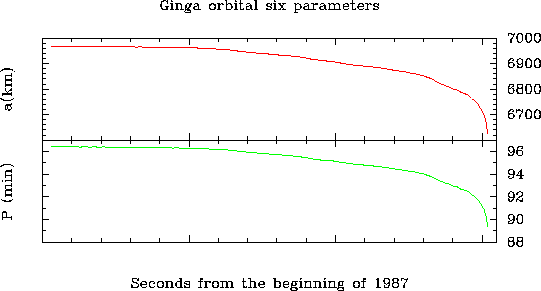 |
ぎんが衛星のように低高度の衛星は、一日に地球の周りを約15周することがわかる。
Ken EBISAWA
2011-02-08
![]() 。
。
![]() も
も![]() ,
, ![]() ,
, ![]() と同じくほぼ一定のはずであるが、
と同じくほぼ一定のはずであるが、![]() は周期的に
変化している。これは、地球が扁平である影響で人工衛星の軌道面が歳差運動をしているためである。
ほぼ円軌道なので、近地点の位置を表わす
は周期的に
変化している。これは、地球が扁平である影響で人工衛星の軌道面が歳差運動をしているためである。
ほぼ円軌道なので、近地点の位置を表わす![]() はあまり意味を持たない。
はあまり意味を持たない。
![]() が減少(衛星が降下)していることがわかる。
また、もともと離心率は小さくほぼ円軌道であったが、衛星が降下するにつれて、さらに
円軌道からのずれが「なまされて」、離心率も減少していることがわかる。
が減少(衛星が降下)していることがわかる。
また、もともと離心率は小さくほぼ円軌道であったが、衛星が降下するにつれて、さらに
円軌道からのずれが「なまされて」、離心率も減少していることがわかる。
![]() から衛星の公転周期が求められる。
地球のシュワルツシルド半径、
から衛星の公転周期が求められる。
地球のシュワルツシルド半径、![]() mmを使うと、以下のように簡単に計算できる。
mmを使うと、以下のように簡単に計算できる。
![]() の関係を図9に示す。
の関係を図9に示す。