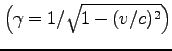 。
物体の運動も、
。
物体の運動も、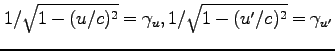 とする。
とする。
先と同じく、![]() 系は
系は![]() 系の
系の![]() 軸方向に、
軸方向に、![]() に対して速度
に対して速度![]() で動いているとする
で動いているとする
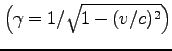 。
物体の運動も、
。
物体の運動も、![]() 系から見て
系から見て![]() 軸方向とし、その速度を
軸方向とし、その速度を![]() とする(
とする(
![]() )。
)。
![]() 系から見た物体の速度を
系から見た物体の速度を![]() とする。
また、
とする。
また、
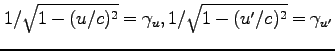 とする。
とする。
ローレンツ変換の式(120)と、四元速度の定義(137)から、
日常生活においては、
物体の移動速度は光速に比べてはるかに小さいので、![]() と近似してよい。すると
上式は
と近似してよい。すると
上式は![]() と言う、見慣れた式になる
と言う、見慣れた式になる![]() 。
。
![]() のときには、
のときには、![]() の値には関わらず、
の値には関わらず、![]() になる。これは光速度不変の原理に他ならない。
になる。これは光速度不変の原理に他ならない。
![]() ,
, ![]() としてみよう。非相対論的に考えると、
としてみよう。非相対論的に考えると、![]() 系から見て、物体は
系から見て、物体は
![]() で遠ざかっていくことになるが、そんなことは実際にはありえない。
式(143は、
で遠ざかっていくことになるが、そんなことは実際にはありえない。
式(143は、![]() を与える。物体の運動の速度が光速を越えることは
ありえないのだ。
を与える。物体の運動の速度が光速を越えることは
ありえないのだ。