


Next: 二体問題
Up: 一般相対性理論
Previous: シュバルツシルト時空
地球の半径はそのシュバルツシルト半径に比べてはるかに大きいから、一般相対性理論の効果は、
日常生活では、ほとんど効いてこない。しかし、非常に精密な測定によって、一般相対性理論が
効いてくることがある。その例がGPS (Glocal Positioning System)である。
GPSは、地球の周りをそれぞれ12時間で周回する24個の衛星を用いている。3個の衛星からの正確な距離が
わかれば、地球上あらゆる場所の位置が正確にわかる。
衛星からの距離は、
光の発射時刻と受信時刻の差に光速を掛けて求める。時刻の補正には4つめの衛星を使う。地球上の
どこからでも、(視界が開けていれば)常に4つの衛星が受信できるように、衛星軌道が
配置されている。
地球表面で自転運動している観測者、GPS衛星上で公転運動している観測者を考える。
式(134)で、どちらの''shell''でも、
自分の座標系では動いていないから、
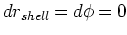 で、
で、
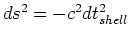 である。十分遠方の観測者がこれを見たとき
である。十分遠方の観測者がこれを見たとき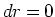 だから、
(135)と合わせて、
だから、
(135)と合わせて、
 |
(139) |
である。よって、
ここで、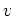 は、地表の自転速度、またはGPS衛星の公転の速度である。
(140)を、地表とGPS衛星について比を取って、
は、地表の自転速度、またはGPS衛星の公転の速度である。
(140)を、地表とGPS衛星について比を取って、
 |
(141) |
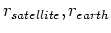 は地球のシュバルツシルト半径に比べて
はるかに大きいから、いくつか近似が可能である。
は地球のシュバルツシルト半径に比べて
はるかに大きいから、いくつか近似が可能である。
まず、
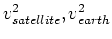 の項を除いて考えよう(これらの効果はマイナーであることが
わかっている)。
この式からただちにわかるように、
の項を除いて考えよう(これらの効果はマイナーであることが
わかっている)。
この式からただちにわかるように、
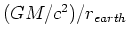 と
と
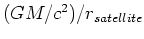 はどちらも非常に小さな数であるが、その違いが無視できない、ということが本質的である。
はどちらも非常に小さな数であるが、その違いが無視できない、ということが本質的である。
GPS衛星の周期が12時間ということから、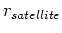 と
と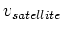 を求めよう。
円運動の公式から
を求めよう。
円運動の公式から![[*]](../../../icons/footnote.png) 、
、
 |
(144) |
 |
(145) |
これを変形して、
 |
(146) |
 |
(147) |
数値を代入して、
 m (2万6600km)、
m (2万6600km)、
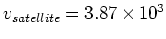 m/s.
m/s.
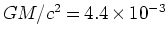 m、
m、
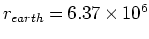 mだから、
(143)に代入して、
mだから、
(143)に代入して、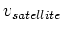 、
、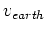 の項を無視すると、
の項を無視すると、
 |
(148) |
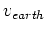 として赤道上の値を使うと、
として赤道上の値を使うと、
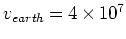 m/86400=463 m/s。
(143)に
m/86400=463 m/s。
(143)に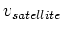 、
、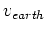 の項も入れて、
の項も入れて、
 |
(149) |
これだけの割合で、地表の時間よりも、人工衛星上の時間のほうが速く進むことがわかる。
一日(86400秒)で、このずれは、38マイクロ秒になる。その間に、光は11kmも進む!
これを補正しないと、GPSは全く使いものにならない。



Next: 二体問題
Up: 一般相対性理論
Previous: シュバルツシルト時空
Ken EBISAWA
2008-01-30
![]() で、
で、
![]() である。十分遠方の観測者がこれを見たとき
である。十分遠方の観測者がこれを見たとき![]() だから、
(135)と合わせて、
だから、
(135)と合わせて、


![]() と
と![]() を求めよう。
円運動の公式から
を求めよう。
円運動の公式から![]() 、
、




![]() m、
m、
![]() mだから、
(143)に代入して、
mだから、
(143)に代入して、![]() 、
、![]() の項を無視すると、
の項を無視すると、

