球対象だから、世界間隔を表わすのに、極座標を用いると便利である。
天体の近く、動径座標![]() の球殻に固定した観測者が計る時間を
の球殻に固定した観測者が計る時間を![]() 、
、
![]() に沿って直接測る距離を
に沿って直接測る距離を![]() とすると、
とすると、
十分遠方の観測者が乗っている座標を![]() とすると、メトリックは
とすると、メトリックは
太陽と地球のシュバルツシルト半径は覚えておこう。
![]() m
m![]() /kg/s
/kg/s![]() 、
、
![]() m/s、太陽質量=
m/s、太陽質量=
![]() kg、
地球質量
kg、
地球質量
![]() kgだから、
太陽のシュバルツシルト半径は、2.95 km、地球の
シュバルツシルト半径は8.87 mm
kgだから、
太陽のシュバルツシルト半径は、2.95 km、地球の
シュバルツシルト半径は8.87 mm![]() 。
。
通常の星(主系列星)は、核融合反応による圧力で形を保っていて、その半径は シュバルツシルト半径よりもはるかに大きい。 中性子星の平均質量は太陽質量の約1.4倍で、中性子間の核力により形を保っていて、 その半径はシュバルツシルト半径よりも大きい。質量が太陽の約3倍以上になると、 中性子間の核力でもその重さを支えられなくなり、重力崩壊を起こしてブラックホールになる。 回転していなりブラックホールの半径(のようなもの)が、シュバルツシルト半径と考えてよい。
(136)は、直接測った動径方向の長さは、円周を![]() で
割った長さよりも長いことを示している。
(137)は、重力が強いところでは、時間の進み方が遅いことを示している。
特にシュバルツシルト半径、
で
割った長さよりも長いことを示している。
(137)は、重力が強いところでは、時間の進み方が遅いことを示している。
特にシュバルツシルト半径、
![]() においては、
においては、
![]() に対しても
に対しても![]() は無限大になる。よって、たとえばブラックホールに
一定間隔で光を出しながらモノが落ちていくようすを無限遠方から眺めると、
シュバルツシルト半径に近づくにつれてその間隔は伸びていき、やがて
無限になる(モノがブラックホールに落ちるところは決っして観測できない)。
は無限大になる。よって、たとえばブラックホールに
一定間隔で光を出しながらモノが落ちていくようすを無限遠方から眺めると、
シュバルツシルト半径に近づくにつれてその間隔は伸びていき、やがて
無限になる(モノがブラックホールに落ちるところは決っして観測できない)。
また、天体の近く![]() で時間間隔
で時間間隔![]() の間に
の間に![]() 個の光波が発射されたとき、
その場所における光の振動数は
個の光波が発射されたとき、
その場所における光の振動数は
![]() 、
無限遠方で観測した同じ光の振動数は
、
無限遠方で観測した同じ光の振動数は![]() であるが、
(137)より、
であるが、
(137)より、
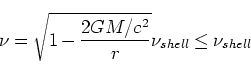 |
(138) |