

Next: シュバルツシルト時空
Up: 一般相対性理論
Previous: 一般相対性理論
互いに等速運動している座標系の間では、式(86)で与えられる
四次元時空中の二点間の「世界間隔」は不変量であった。二つの系の間の座標変換(ローレンツ
変換)は、ベクトルの長さを変えない、四次元時空における回転を表す「直交変換」と考えても良いことを
見てきた。これは、系が加速度運動をしておらず、重力を及ぼすモノが存在しない場合にのみ
成立し、この条件が成立している座標系を慣性系と呼ぶ。
慣性系では「時空が平坦」なので、世界間隔は不変である。
慣性系においては、ニュートンの第一法則が成立し、
「静止しているモノは静止しつづけ、等速運動しているモノは等速運動しつづける」。
現実の世界には完全な慣性系は存在しないが、加速度運動による慣性力と重力は区別できないという
等価原理によって、重力と慣性力を打ち消しあった、局所慣性系を定義することができる。
たとえば、
宇宙空間に浮かんで、いろいろな
天体からの重力に身を任せている宇宙船の中は局所慣性系である。その宇宙船に対して等速運動している
局所慣性系とのあいだの座標変換はローレンツ変換で与えられる。
慣性系は局所的にしか存在できないことは、以下の思考実験でわかる。
遠方から地球に向かって自由落下する宇宙船を考えよう。あるいは、綱の切れたエレベーターの中でも良い。
その中は局所慣性系になっている
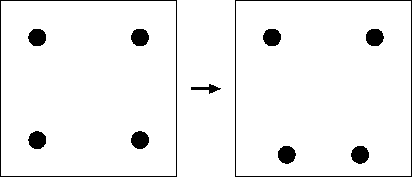
(いわゆる「無重力状態![[*]](../../../icons/footnote.png) )。ボールを4つ等間隔に配置する。
)。ボールを4つ等間隔に配置する。
もしこれが完全な慣性系ならば、ボールの間隔は変化しないはずだが、
それぞれのボールは地球の中心に向かって落ちていき、地球の中心に近いほうが
重力加速度は大きいので、やがてボール間の横方向の間隔は縮み、
縦方向の間隔は伸びる![[*]](../../../icons/footnote.png) 。
。
一般に、
グローバルな慣性系は定義できない(時空は一様でない)ので、(86)は成立せず、
代わりに、二つの局所慣性系座標の間に、
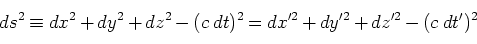 |
(133) |
が成立する。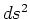 をメトリック(計量)と呼ぶ。
一般相対性理論によれば、任意の座標変換に対して、局所的な世界間隔は不変である。
をメトリック(計量)と呼ぶ。
一般相対性理論によれば、任意の座標変換に対して、局所的な世界間隔は不変である。
Ken EBISAWA
2008-01-30
![]() )。ボールを4つ等間隔に配置する。
)。ボールを4つ等間隔に配置する。