僴僯僇儉僒儞僪僀僢僠斅偲桳尷梫慺朄夝愅
丂丂丂搶嫗搒棫壢妛媄弍戝妛岺妛晹丂丂搉曈丂捈峴
仧偼偠傔偵
丂尰嵼偺峲嬻塅拡暘栰偵偍偄偰丆寉検壔偺娤揰偐傜丆暋崌嵽椏偲僒儞僪僀僢僠峔憿偼晄壜寚側傕偺偲側偭偰偄傞丅暋崌嵽椏偵偮偄偰偼丆偙偺棑偱傕偡偱偵壗搙偐庢傝忋偘傜傟偰偄傞偺偱丆偙偙偱偼僒儞僪僀僢僠斅偵偮偄偰徯夘偡傞丅僒儞僪僀僢僠斅偼丆寉偔偰崉惈偺掅偄怱嵽(僐傾)傪崉惈丒嫮搙偺崅偄敄偄斅偱嫴傫偩傕偺偱偁傝丆昞旂偲僐傾偼僔乕僩宆偺愙拝嵻偱愙拝偝傟傞丅傾儖儈昞旂/傾儖儈僴僯僇儉僐傾偺僒儞僪僀僢僠斅偑懡偔巊傢傟偰偄傞偑丆寉検偐偮崅嫮搙丆崅崉惈偺梫媮偑嫮偄応崌偵偼丆僐傾傪岤偔偟丆摨帪偵昞旂偵俠俥俼俹(扽慺慇堐嫮壔僾儔僗僠僢僋)偑梡偄傜傟傞丅俵-倁偺僲乕僘僼僃傾儕儞僌偼丆婎杮揑偵偼昞旂偑俠俥俼俹偱僐傾偑傾儖儈僴僯僇儉偱偁傞僒儞僪僀僢僠斅偱偁傞丅偨偩偟塹惎偲偺揹攇偵傛傞岎怣傪峴偆偨傔丆暿側慺嵽偱偱偒偰偄傞捠徧乬憢乭偲屇偽傟傞晹暘偑偁傝丆偦偙偼昞旂偵俧俥俼俹(僈儔僗慇堐嫮壔僾儔僗僠僢僋)丆僐傾偵僲乕儊僢僋僗(働僽儔慇堐嫮壔僾儔僗僠僢僋)傪梡偄偰揹攇偺摟夁惈傪妋曐偟偰偄傞丅傑偨丆俙俽俿俼俷-俠丆俽俷俴俙俼-俙側偳偺塹惎偱偺庡峔憿懱偼丆傎偲傫偳偑僒儞僪僀僢僠斅偱偱偒偰偄傞丅偙偺傛偆偵寉検偱嬋偘崉惈偑旕忢偵崅偔丆嬋偘偁傞偄偼埑弅傪庴偗傞晹嵽偲偟偰懡梡偝傟丆嫮搙偽偐傝偱側偔嵗孅丆屌桳怳摦悢側偳偺崉惈梫媮偐傜傕桳棙偱偁傞丅丂堦曽丆寁嶼婡偺媫懍側恑曕偲憡傑偭偰丆桳尷梫慺朄(俥俤俵)傪戙昞偲偡傞悢抣夝愅朄偑條乆側暘栰偱巊傢傟傞傛偆偵側偭偰偄傞丅峲嬻塅拡偺峔憿愝寁偵偍偄偰偼俶俙俽俙偑奐敪偟偨斈梡戝宆俥俤俵僜儖僶乕俶俙俽俿俼俙俶偑昁偢偲尵偭偰偄偄傎偳偵梡偄傜傟偰偄傞丅偟偐偟側偑傜丆偝傜側傞寉検壔偺梫媮偼丆僒儞僪僀僢僠斅偵尷偭偰傒偰傕丆捠忢偺夝愅偱偼捛偄偮偐側偄尰徾偑婲偙偭偰偒偰偄傞丅偙偙偱偼偦偺撪偺擇偮偺尰徾偲丆夝愅寢壥偵偮偄偰弎傋傞丅
仧嵶偐偄擬嵗孅(僨傿儞僾儖)偺栤戣
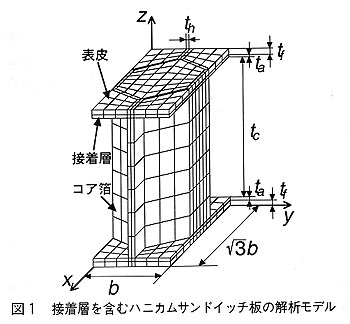 丂恾侾偵僴僯僇儉僐傾偺僙儖侾偮暘偺桳尷梫慺儌僨儖傪帵偡丅嵟傕奜懁偵岤偝 tf 偺昞旂偑偁傝丆師偵岤偝 ta 偺愙拝僔乕僩偑偁傝偦偺壓偵崅偝 tc 偺僐傾偑偁傞丅拞棫幉(拞怱)偐傜棧傟偨強偵崉惈偺崅偄嵽椏傪攝抲偡傟偽傛偄偺偱丆塹惎丒儘働僢僩偺峔憿偺傛偆偵丆寉検壔傪捛媦偡傞応崌偼丆昞旂偵崅崉惈僞僀僾偺俠俥俼俹傪巊偄丆僐傾崅偝 tc 傪戝偒偔丆昞旂岤偝 tf 傪彫偝偔偡傞丅偙傟偵傛傝懢梲揹抮僷僪儖側偳偵偼昞旂岤偝偑0.1咢偱丆僐傾崅偝偑俀僀儞僠(50.8咢)偲偄偆傛偆側傕偺傑偱巊傢傟偰偄傞丅昞旂偲僐傾偼120亷偱愙拝偝傟傞偑忢壏偵栠偡娫偵丆擬朿挘學悢偺堘偄偐傜(俠俥俼俹偼傎偲傫偳侽丆傾儖儈偼俇 x 10-6/亷偱偁傝愙拝嵻偼偝傜偵懡偒側抣偱偁傞)昞旂偵埑弅丆僐傾偵堷挘偺巆棷擬墳椡偑敪惗偟丆忋婰偺條偵昞旂偑嬌傔偰敄偄応崌偵偼丆恾俀偵帵偡傛偆側昞旂偵僐傾偺廃婜偵堦抳偡傞嵶偐偄擬嵗孅(僨傿儞僾儖)偑惗偠丆斅偲偟偰偺崉惈丆埑弅嵗孅壸廳偑戝偒偔掅壓偡傞丅傑偨丆忢壏偱偼偙傟偑尠挊偱柍偄応崌偱傕丆塅拡嬻娫偱偼擔塭偵側傞帪側偳偵偼壏搙偑偝傜偵掅壓偟僨傿儞僾儖偑惗偠傞丅懢梲揹抮僙儖傪揬傞応崌偵偼丆偔傏傒偵愙拝嵻偑擖傝偡偓偰丆偣偭偐偔偺寉検壔偑戜柍偟偲側傞側偳偺栤戣傕惗偠傞丅
丂恾侾偵僴僯僇儉僐傾偺僙儖侾偮暘偺桳尷梫慺儌僨儖傪帵偡丅嵟傕奜懁偵岤偝 tf 偺昞旂偑偁傝丆師偵岤偝 ta 偺愙拝僔乕僩偑偁傝偦偺壓偵崅偝 tc 偺僐傾偑偁傞丅拞棫幉(拞怱)偐傜棧傟偨強偵崉惈偺崅偄嵽椏傪攝抲偡傟偽傛偄偺偱丆塹惎丒儘働僢僩偺峔憿偺傛偆偵丆寉検壔傪捛媦偡傞応崌偼丆昞旂偵崅崉惈僞僀僾偺俠俥俼俹傪巊偄丆僐傾崅偝 tc 傪戝偒偔丆昞旂岤偝 tf 傪彫偝偔偡傞丅偙傟偵傛傝懢梲揹抮僷僪儖側偳偵偼昞旂岤偝偑0.1咢偱丆僐傾崅偝偑俀僀儞僠(50.8咢)偲偄偆傛偆側傕偺傑偱巊傢傟偰偄傞丅昞旂偲僐傾偼120亷偱愙拝偝傟傞偑忢壏偵栠偡娫偵丆擬朿挘學悢偺堘偄偐傜(俠俥俼俹偼傎偲傫偳侽丆傾儖儈偼俇 x 10-6/亷偱偁傝愙拝嵻偼偝傜偵懡偒側抣偱偁傞)昞旂偵埑弅丆僐傾偵堷挘偺巆棷擬墳椡偑敪惗偟丆忋婰偺條偵昞旂偑嬌傔偰敄偄応崌偵偼丆恾俀偵帵偡傛偆側昞旂偵僐傾偺廃婜偵堦抳偡傞嵶偐偄擬嵗孅(僨傿儞僾儖)偑惗偠丆斅偲偟偰偺崉惈丆埑弅嵗孅壸廳偑戝偒偔掅壓偡傞丅傑偨丆忢壏偱偼偙傟偑尠挊偱柍偄応崌偱傕丆塅拡嬻娫偱偼擔塭偵側傞帪側偳偵偼壏搙偑偝傜偵掅壓偟僨傿儞僾儖偑惗偠傞丅懢梲揹抮僙儖傪揬傞応崌偵偼丆偔傏傒偵愙拝嵻偑擖傝偡偓偰丆偣偭偐偔偺寉検壔偑戜柍偟偲側傞側偳偺栤戣傕惗偠傞丅
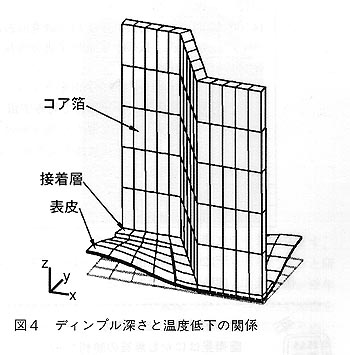
 丂偙偺尰徾偼嬌傔偰暋嶨偱偁傞丅壏搙傪壓偘偰偄偔偲丆昞旂偺擬偵傛傞埑弅墳椡偑憹壛偟丆偦傟偵傛傝嬋偘曄宍偑戝偒偔側傞偑丆摨帪偵偦偺曄宍偵傛傝墳椡偑娚榓偝傟傞丅擬墳椡夝愅偲戝曄宍夝愅偲堎曽惈乮昞旂偼堦憌偱偼側偔堎側傞摿惈偺憌偐傜側傞愊憌斅偱偁傞乯偺栤戣傪摨帪偵夝偐偹偽側傜側偄丅恾俁偵丆b亖9.5咢丆tf亖0.1咢丆tc亖20咢丆th亖0.05咢偺応崌偺夝愅寢壥傪帵偡丅廲幉偼壏搙偺掅壓検偱墶幉偼僨傿儞僾儖怺偝偱偁傞丅愙拝憌偑柍偄応崌偲0.1咢偺愙拝憌傪帩偮応崌傪斾妑偡傞丅愙拝憌偑柍偟偺応崌偼壏搙掅壓偑50亷晅嬤偱僨傿儞僾儖偑怺偔側傝巒傔偦偺屻媫寖偵憹壛偟丆嵟廔揑偵偼180兪m偵傕払偡傞丅堦曽丆0.1咢偺愙拝憌傪帩偮応崌偼80亷晅嬤傑偱僨傿儞僾儖偼傎偲傫偳怺偔側傜偢丆偦偺屻娚傗偐偵憹壛偟偰偄偔偑丆120亷偱傕75兪m偵偡偓側偄丅偙偺寢壥偐傜偼丄愙拝憌偼埨慡懁偵摥偔傛偆偵尒偊傞丅偲偙傠偑丆幚嵺偵塹惎峔憿側偳偵巊傢傟傞傕偺偱偼丆傛傝偄偭偦偆偺寉検壔偺偨傔偝傜偵敄偄僔乕僩宆愙拝嵻傪巊偄丆愙拝嵻偼峝壔屻偵偼僐傾敁 偲昞旂偺愙崌揰晅嬤偺傒偵廤傑傞傛偆偵摿庩側張棟偑側偝傟偰偄傞丅偦偺儌僨儖壔傪偟偨偺偑恾係偱偁傝丆嵟廔揑側擬曄宍(幚嵺偺50攞偵奼戝偟偰偁傞)傪摨帪偵帵偡丅偙偺條側儌僨儖壔傪峴偆偲丆恾俁偵乬寠奐偒0.2咢乭偲偟偰帵偡傛偆偵丄僨傿儞僾儖偼壏搙掅壓偑彮側偄撪偐傜偝傜偵戝偒偔敪惗偡傞帠偵側傝丆傛傝怺崗側帠懺偱偁傞帠偑傢偐傞丅
丂偙偺尰徾偼嬌傔偰暋嶨偱偁傞丅壏搙傪壓偘偰偄偔偲丆昞旂偺擬偵傛傞埑弅墳椡偑憹壛偟丆偦傟偵傛傝嬋偘曄宍偑戝偒偔側傞偑丆摨帪偵偦偺曄宍偵傛傝墳椡偑娚榓偝傟傞丅擬墳椡夝愅偲戝曄宍夝愅偲堎曽惈乮昞旂偼堦憌偱偼側偔堎側傞摿惈偺憌偐傜側傞愊憌斅偱偁傞乯偺栤戣傪摨帪偵夝偐偹偽側傜側偄丅恾俁偵丆b亖9.5咢丆tf亖0.1咢丆tc亖20咢丆th亖0.05咢偺応崌偺夝愅寢壥傪帵偡丅廲幉偼壏搙偺掅壓検偱墶幉偼僨傿儞僾儖怺偝偱偁傞丅愙拝憌偑柍偄応崌偲0.1咢偺愙拝憌傪帩偮応崌傪斾妑偡傞丅愙拝憌偑柍偟偺応崌偼壏搙掅壓偑50亷晅嬤偱僨傿儞僾儖偑怺偔側傝巒傔偦偺屻媫寖偵憹壛偟丆嵟廔揑偵偼180兪m偵傕払偡傞丅堦曽丆0.1咢偺愙拝憌傪帩偮応崌偼80亷晅嬤傑偱僨傿儞僾儖偼傎偲傫偳怺偔側傜偢丆偦偺屻娚傗偐偵憹壛偟偰偄偔偑丆120亷偱傕75兪m偵偡偓側偄丅偙偺寢壥偐傜偼丄愙拝憌偼埨慡懁偵摥偔傛偆偵尒偊傞丅偲偙傠偑丆幚嵺偵塹惎峔憿側偳偵巊傢傟傞傕偺偱偼丆傛傝偄偭偦偆偺寉検壔偺偨傔偝傜偵敄偄僔乕僩宆愙拝嵻傪巊偄丆愙拝嵻偼峝壔屻偵偼僐傾敁 偲昞旂偺愙崌揰晅嬤偺傒偵廤傑傞傛偆偵摿庩側張棟偑側偝傟偰偄傞丅偦偺儌僨儖壔傪偟偨偺偑恾係偱偁傝丆嵟廔揑側擬曄宍(幚嵺偺50攞偵奼戝偟偰偁傞)傪摨帪偵帵偡丅偙偺條側儌僨儖壔傪峴偆偲丆恾俁偵乬寠奐偒0.2咢乭偲偟偰帵偡傛偆偵丄僨傿儞僾儖偼壏搙掅壓偑彮側偄撪偐傜偝傜偵戝偒偔敪惗偡傞帠偵側傝丆傛傝怺崗側帠懺偱偁傞帠偑傢偐傞丅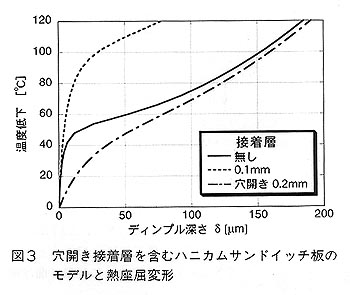
 丂寉検壔偵傛傞暿側栤戣偲偟偰丆僴僯僇儉僒儞僪僀僢僠斅偑嬻婥椡偵傛傝塭嬁傪庴偗丆偦傟偑柍帇偱偒側偔側傞帠傕嬤擭敪惗偟偰偒偰偄傞丅桳柤側偺偼丆戝偒側懢梲揹抮僷僪儖傑偨偼傾儞僥僫偑抧忋偱偺怳摦帋尡偵偍偄偰嬻婥拞偱怳摦偡傞嵺偵丆昞柺嬤偔偺嬻婥傪墴偟偺偗傞帠偱傒偐偗偺幙検偑憹偊丆嫟怳怳摦悢偑嬻婥偑柍偄応崌偵妑傋偰掅壓偡傞帠偲偟偰抦傜傟偰偄傞丅偙偺栤戣偵偮偄偰偼晅壛幙検偵傛傞嬤帡夝朄偵傛傝斾妑揑梕堈偵張棟偝傟偰偒偰偄傞丅堦曽丆嬤擭塿乆戝宆壔丆寉検壔偝傟偰偒偨懢梲揹抮僷僪儖偼丆懪偪忋偘帪偵偼 幹暊偺傛偆偵愜傝忯傒廂擺偝傟傞帠偑懡偔側偭偰偄傞丅 偙傟傜偼丆懪偪忋偘帪偺怳摦偵嵺偟丆僷僱儖娫偵嫴傑傟偨嬻婥憌偐傜戝偒側塭嬁傪庴偗傞丅幚嵺偵丆暯惉係擭偵懪偪忋偘傜傟偨抧媴帒尮塹惎(傆傛偆)侾崋偵搵嵹偝傟偰偄偨崌惉奐岥儗乕僟乕偼丆廲2.3m x 墶1.4m x 岤偝22咢丆幙検15哃/枃偺僴僯僇儉僒儞僪僀僢僠斅偑6咢偺娫妘偱俉枃愜傝忯傑傟偨傕偺偱偁偭偨丅怳摦帋尡偵偍偄偰丆柺奜曽岦偺嫟怳怳摦悢偼61Hz偱偁偭偨偑丆嬻婥椡傪峫椂偟側偄桳尷梫慺朄夝愅偱偼52.1Hz偲戝偒側嵎偑惗偠偨丅娫偺嬻婥憌偑斅偺怳摦偵懳偟偰嬻婥僶僱偲偟偰嶌梡偟丆嫟怳怳摦悢傪偙偺傛偆偵17亾傕崅偔偟偨丅峔憿懱偺嫮搙曐徹摍傪帋尡偺傒偱偺妋擣偑晄壜擻偱丆偐側傝偺晹暘傪夝愅偵傛傝峴偭偰偄傞塹惎峔憿偱偼戝偒側栤戣偲側傞丅
丂寉検壔偵傛傞暿側栤戣偲偟偰丆僴僯僇儉僒儞僪僀僢僠斅偑嬻婥椡偵傛傝塭嬁傪庴偗丆偦傟偑柍帇偱偒側偔側傞帠傕嬤擭敪惗偟偰偒偰偄傞丅桳柤側偺偼丆戝偒側懢梲揹抮僷僪儖傑偨偼傾儞僥僫偑抧忋偱偺怳摦帋尡偵偍偄偰嬻婥拞偱怳摦偡傞嵺偵丆昞柺嬤偔偺嬻婥傪墴偟偺偗傞帠偱傒偐偗偺幙検偑憹偊丆嫟怳怳摦悢偑嬻婥偑柍偄応崌偵妑傋偰掅壓偡傞帠偲偟偰抦傜傟偰偄傞丅偙偺栤戣偵偮偄偰偼晅壛幙検偵傛傞嬤帡夝朄偵傛傝斾妑揑梕堈偵張棟偝傟偰偒偰偄傞丅堦曽丆嬤擭塿乆戝宆壔丆寉検壔偝傟偰偒偨懢梲揹抮僷僪儖偼丆懪偪忋偘帪偵偼 幹暊偺傛偆偵愜傝忯傒廂擺偝傟傞帠偑懡偔側偭偰偄傞丅 偙傟傜偼丆懪偪忋偘帪偺怳摦偵嵺偟丆僷僱儖娫偵嫴傑傟偨嬻婥憌偐傜戝偒側塭嬁傪庴偗傞丅幚嵺偵丆暯惉係擭偵懪偪忋偘傜傟偨抧媴帒尮塹惎(傆傛偆)侾崋偵搵嵹偝傟偰偄偨崌惉奐岥儗乕僟乕偼丆廲2.3m x 墶1.4m x 岤偝22咢丆幙検15哃/枃偺僴僯僇儉僒儞僪僀僢僠斅偑6咢偺娫妘偱俉枃愜傝忯傑傟偨傕偺偱偁偭偨丅怳摦帋尡偵偍偄偰丆柺奜曽岦偺嫟怳怳摦悢偼61Hz偱偁偭偨偑丆嬻婥椡傪峫椂偟側偄桳尷梫慺朄夝愅偱偼52.1Hz偲戝偒側嵎偑惗偠偨丅娫偺嬻婥憌偑斅偺怳摦偵懳偟偰嬻婥僶僱偲偟偰嶌梡偟丆嫟怳怳摦悢傪偙偺傛偆偵17亾傕崅偔偟偨丅峔憿懱偺嫮搙曐徹摍傪帋尡偺傒偱偺妋擣偑晄壜擻偱丆偐側傝偺晹暘傪夝愅偵傛傝峴偭偰偄傞塹惎峔憿偱偼戝偒側栤戣偲側傞丅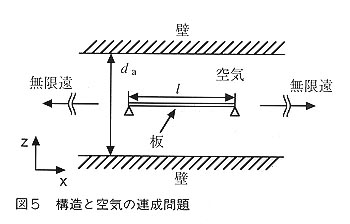 丂廬棃偐傜憿慏側偳偺暘栰偵偍偄偰塼懱(廳偔埑弅偝傟側偄)偲峔憿偺楢惉栤戣偼斾妑揑懡偔尋媶偝傟偰偒偰偄傞偑丆嬻婥摍偺婥懱偲偺傕偺偼傎偲傫偳柍偄丅変乆偼丆嬻婥偲峔憿偺楢惉怳摦偺栤戣傪桳尷梫慺朄偵傛傝摑堦揑偵夝愅偡傞偙偲傪帋傒偨丅夝愅偟偨栤戣偺堦椺傪恾俆偵帵偡丅偙偙偱偼夝愅偺娙扨壔偺偨傔偵丆師偺壖掕傪傕偆偗偨丅懡憌斅傪堦枃偺廮擃側(傕偪傠傫旕忢偵寉偄)斅偲丆椉椬偵側傞崉惈偺崅偄斅(崉暻)偱儌僨儖壔偡傞丅偝傜偵偦傟傜偼巻柺偵悅捈側曽岦偵柍尷偵懕偄偰偄傞偲偡傞帠偵傛傝丆擇師尦栤戣偲偟偰埖偭偨丅偙偙偱斅(椑)偺挿偝傪侾偲偟丆嬻婥憌偺岤偝傪 da 偲偟丆偦傟傜傪曄偊偰寁嶼偟偨丅嵟掅師嫟怳怳摦悢偺寢壥傪恾俇偵帵偡丅
丂廬棃偐傜憿慏側偳偺暘栰偵偍偄偰塼懱(廳偔埑弅偝傟側偄)偲峔憿偺楢惉栤戣偼斾妑揑懡偔尋媶偝傟偰偒偰偄傞偑丆嬻婥摍偺婥懱偲偺傕偺偼傎偲傫偳柍偄丅変乆偼丆嬻婥偲峔憿偺楢惉怳摦偺栤戣傪桳尷梫慺朄偵傛傝摑堦揑偵夝愅偡傞偙偲傪帋傒偨丅夝愅偟偨栤戣偺堦椺傪恾俆偵帵偡丅偙偙偱偼夝愅偺娙扨壔偺偨傔偵丆師偺壖掕傪傕偆偗偨丅懡憌斅傪堦枃偺廮擃側(傕偪傠傫旕忢偵寉偄)斅偲丆椉椬偵側傞崉惈偺崅偄斅(崉暻)偱儌僨儖壔偡傞丅偝傜偵偦傟傜偼巻柺偵悅捈側曽岦偵柍尷偵懕偄偰偄傞偲偡傞帠偵傛傝丆擇師尦栤戣偲偟偰埖偭偨丅偙偙偱斅(椑)偺挿偝傪侾偲偟丆嬻婥憌偺岤偝傪 da 偲偟丆偦傟傜傪曄偊偰寁嶼偟偨丅嵟掅師嫟怳怳摦悢偺寢壥傪恾俇偵帵偡丅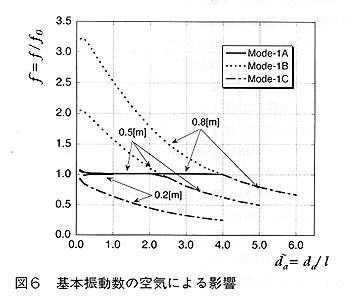 墶幉偼嬻婥憌偺暆傪斅偺挿偝偱妱偭偨柍師尦嬻婥憌岤偝偱偁傝丆廲幉偼嬻婥傪峫椂偟偨帪偺怳摦悢傪嬻婥椡偑柍偄帪偺傕偺偱柍師尦壔偟偨怳摦悢偱偁傞丅斅偺挿偝偑0.2m偺傛偆偵抁偄帪偵偼怳摦悢偼忢偵侾傛傝彫偝偔丆嬻婥偺晅壛幙検岠壥偵傛傝怳摦悢偼掅壓偡傞偙偲偑傢偐傞丅0.5m偺応崌偼丆嬻婥憌偑敄偄帪偵偼僶僱岠壥偱怳摦悢偼崅偔側傝丆嬻婥憌偑岤偄帪偵偼晅壛幙検岠壥偵傛傝怳摦悢偼掅壓偡傞丅0.8m偺応崌傕摨條偱偁傞丅嬻婥憌偑敄偄応崌偵儌乕僪偑擇偮懚嵼偡傞偺偼嬻婥偺棳傟偺嫇摦偑堎側傞偨傔偱偁傞丅偙偺帠偐傜丆嬻婥偺晅壛幙検岠壥偲僶僱岠壥偑偳偆偄偆応崌偵偳偺傛偆偵尰傟傞偐傪帵偡偙偲偑偱偒偨丅
墶幉偼嬻婥憌偺暆傪斅偺挿偝偱妱偭偨柍師尦嬻婥憌岤偝偱偁傝丆廲幉偼嬻婥傪峫椂偟偨帪偺怳摦悢傪嬻婥椡偑柍偄帪偺傕偺偱柍師尦壔偟偨怳摦悢偱偁傞丅斅偺挿偝偑0.2m偺傛偆偵抁偄帪偵偼怳摦悢偼忢偵侾傛傝彫偝偔丆嬻婥偺晅壛幙検岠壥偵傛傝怳摦悢偼掅壓偡傞偙偲偑傢偐傞丅0.5m偺応崌偼丆嬻婥憌偑敄偄帪偵偼僶僱岠壥偱怳摦悢偼崅偔側傝丆嬻婥憌偑岤偄帪偵偼晅壛幙検岠壥偵傛傝怳摦悢偼掅壓偡傞丅0.8m偺応崌傕摨條偱偁傞丅嬻婥憌偑敄偄応崌偵儌乕僪偑擇偮懚嵼偡傞偺偼嬻婥偺棳傟偺嫇摦偑堎側傞偨傔偱偁傞丅偙偺帠偐傜丆嬻婥偺晅壛幙検岠壥偲僶僱岠壥偑偳偆偄偆応崌偵偳偺傛偆偵尰傟傞偐傪帵偡偙偲偑偱偒偨丅