赤ちゃん星が作りだす巨大爆発現象を理解しよう
目次
1. はじめに
教材を進めていくために必要なワークシート(PDF)
2. 初級編 〜 画像を見てみよう
3. 中級編 〜 X線強度の変化を見てみよう
4. 上級編 〜 吸収量、プラズマの温度、X線の明るさを出してみよう
5. 達人編 〜 太陽フレアと比較をしてみよう
6. 余力があれば ...
答え
所要時間 2時間程度(個人差があります)
1. はじめに 10分、2. 初級編 30分、3. 中級編 30分、4. 上級編 30分、5. 達人編 20分、6. 余力があれば ...
初級編まででもいいですが、ぜひ最後まで到達して、赤ちゃん星が作り出す爆発はすごいものだと実感してください。
1. はじめに
1.1. 星の誕生の舞台
星は、暗黒星雲と呼ばれる漆黒の闇の中で生まれます。そこは何もないから暗いのではなく、 零下250度の極寒の分子ガスや塵がぎっしりと詰まっている場所なのです。 可視光線では暗い暗黒星雲も、電波で観測すれば明々と輝いています。 それは、可視光を遮る極低温の塵自身が電波を放出するためです。このような冷たい物質の中で生まれる星の赤ちゃん(原始星)はどんな姿で何をしているのでしょうか? 実は残念ながら、 星の誕生の瞬間とその後しばらくは、降り積もり、吹き飛ぶガスで幾重にも遮られ、ほとんど見ることはできません。電波や赤外線で見えるのは「新生児」 でなく周辺のガス、いわば「ゆりかご」にすぎないのです。
では、X線でなら星の赤ちゃん達を見ることができるのでしょうか? 極低温の星の誕生の舞台は、X線を放つような高エネルギー現象とは一見無縁に思えます。本当に見えないのか、実際にこの誕生の現場をX線で見てみることにしましょう。
1.2. へびつかい座 ρ(ロー)暗黒星雲(rho Oph)
この宇宙には数多くの銀河が存在します。私たちが住む太陽系はそのような銀河のひとつ、天の川銀河の片隅にあります。下の図は可視光でその天の川銀河を太陽系の方向から真横に眺めた絵です。白いところが太陽のような星が沢山存在する場所であり、黒く見えるのがまさしく暗黒星雲です。
銀河系の中には、たくさんの星が存在します。それ以外の星と星の間は何があるのでしょうか? 全くの真空状態なのでしょうか? 確かに地球上の真空ポンプでは実現できないぐらいの真空状態ですが、ごくわずかながらガス(気体)とダスト(宇宙塵;固体微粒子)とよばれる星間物質が存在しています。この星間物質の分布は一様ではなく、特に密度の高い領域も存在します。このような星間物質の密度の高い領域が、背景の星の光や、散光星雲の光をさえぎって暗く(シルエットとして)見えます。これが暗黒星雲の正体なのです。

へびつかい座ρ暗黒星雲の可視光の画像(参考:Mellinger 2009)
この教材では、上の図にあるように「へびつかい座ρ暗黒星雲」を例として取り上げます。へびつかい座はさそり座の近くにある日本でも夏に見られる星座です。ここにある暗黒星雲は、私たちの銀河中心の方向にあり、また距離も145パーセク(473光年、4.47×1018 m)と近いため、数多くの研究がなされています。
1.3. X線天文衛星「チャンドラ」
アメリカのX線天文衛星「チャンドラ」で撮影された、へびつかい座暗黒星雲のデータを解析しましょう。チャンドラは、1999年にNASAが打ち上げたX線天文衛星で、角分解能が非常に優れた特徴を持っています。そのため、とてもきれいなX線画像を得ることができます。ここでは「チャンドラ」に搭載されたX線CCDカメラで得たデータを使いましょう。

X線天文衛星「チャンドラ」のイラスト(NASAより)
1.4. ワークシートをプリントしよう
こちらに教材を進めていくために必要なワークシート(PDF)がありますので、まずはプリントしましょう。
Questionと書かれたところに自分で答えを書いてみてください。そして、Questionをクリックして、答えを確認をしてください。
2. 初級編 〜 画像を見てみよう
2.1. ソフトとデータを用意しよう
データ解析には、「SAOImage ds9」と「fv FITS viewer」というソフトだけを使って進めていきます。どちらのソフトも天文学者が実際に解析に使用しているソフトです。 データ解析のページを参考に利用してください。
・ SAOImage ds9:fitsファイルの画像の表示に使います。この教材ではバージョン5.7を使って解説しています。
自分の使っているOS用のバイナリーを用意してください。
なお、Windowsでは、とある場所に解凍されるだけなので、ds9のショートカットをデスクトップに作っておくと便利でしょう。
・ fv FITS viewer :
fitsファイル形式で光子の抽出、イベント数の解析、スペクトルやライトカーブの表示に使います。
注意!
なお、バージョン5.*ではとある作業でバグがあるため、ここでは若干古いですが、バージョン4.4のものを必ず使ってください。
この解説もバージョン4.4 用のものです。
次に、へびつかい座暗黒星雲のデータ「RhoOphCore.fits」をあなたのパソコンにダウンロードしましょう。右クリックで保存してください。なお、Windowsでは、「デスクトップ」に保存してしまうと開けないので、「マイ ドキュメント」など、わかりやすい場所に保存してください。
アメリカのX線天文衛星「チャンドラ」は、星の赤ちゃんが生まれている現場である「へびつかい座暗黒星雲」を2000年に観測しています。このデータを調べてみましょう。
2.2. 星の赤ちゃんはX線で見えるかな?
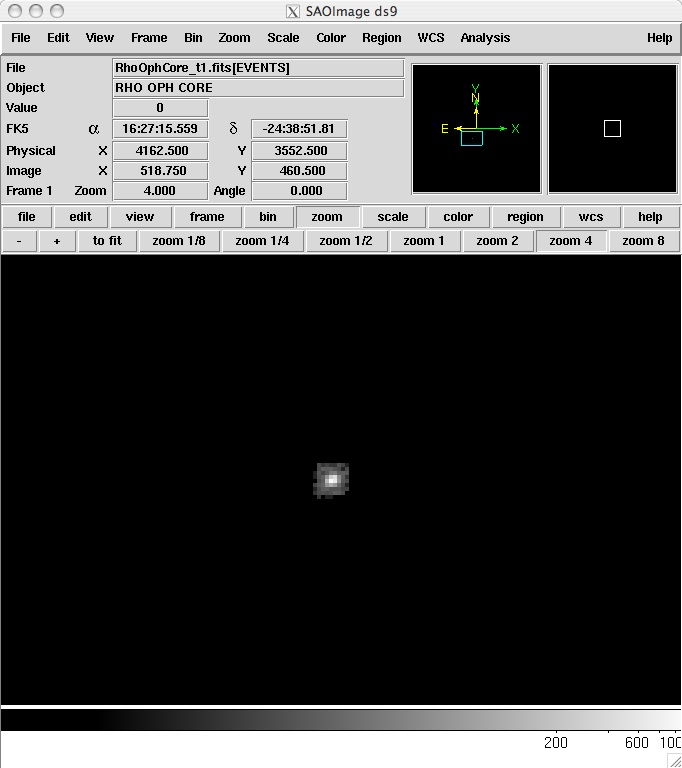
ds9はX線の光子が届いた位置を表示させるためのソフトです。まず、ds9を使ってX線画像を見てみましょう。 星の赤ちゃんは、暗黒星雲のど真ん中で生まれているはずです。他の波長では全く見ることのできない星の赤ちゃんはX線で見えるでしょうか? 明るいのでしょうか? 確認してみましょう。ds9を起動し、File -> open の順でクリックし、RhoOphCore.fitsを開いてください。binをblock 4、scaleはlog、 zoomは2くらいにすると見やすいです。なお、下図の大きな○のところにある水色の□で、表示する位置を調整することができます。
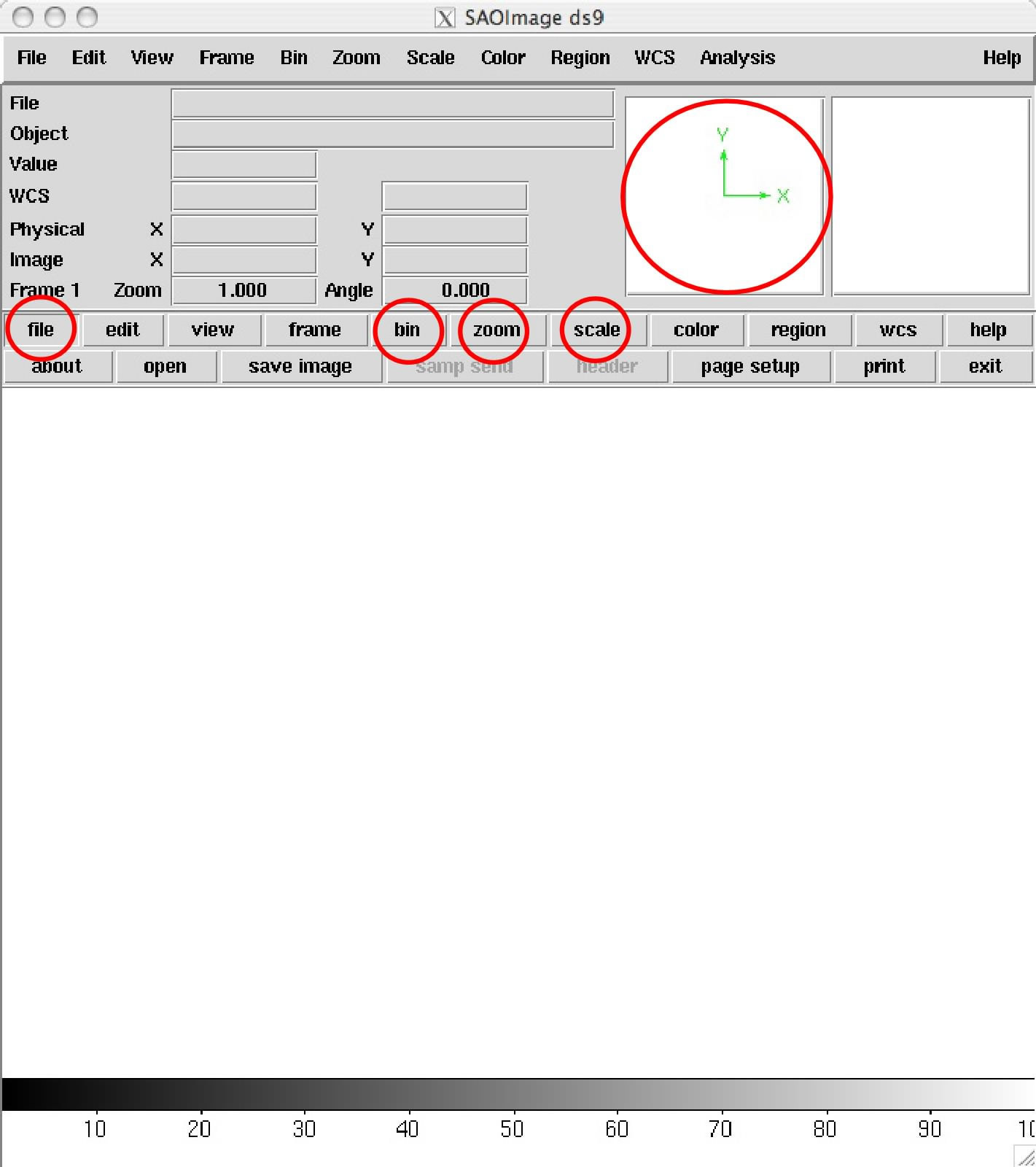
Question 2.2. 画像からどうなりましたか? どんなことが分かりますか?
2.3. 動画を作ってみよう
さて、2.2. で表示した画像は、105 秒(約1.2日)もの積分時間で撮像されたX線写真です。しかし、観測データには光子一個一個がCCDカメラに到来した時刻が書かれていますので、時刻を細分割して、ある時間帯に来た光子だけを取り出すこともできます。それを順次行い、ぱらぱら漫画のように、ds9 で順に表示させれば、X線動画のできあがりです。この暗黒星雲全体としてはどのようなX線の変動が見られるでしょうか。
まずfvを使って、ある時間帯に来た光子だけでイメージを作ります。今回は、20 ksec(20000秒)毎に時間を分割して5つのファイルを作りましょう。fvを起動させ、「Open File」を選んでRhoOphCore.fitsを開き、Allをクリックします。
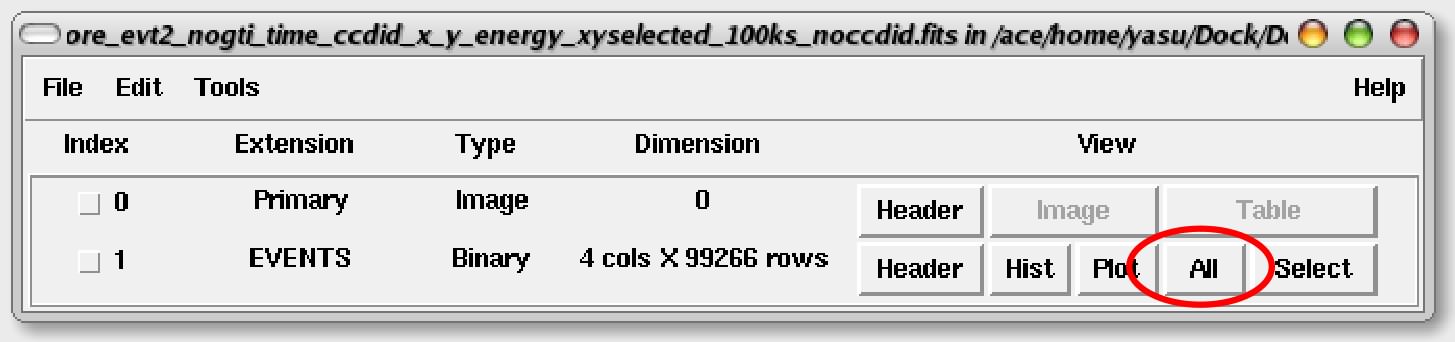
Edit→Select Rows…を選択し、面画が出たら、=の右側に、
『0<time&&time<=20000』と入力し、Selectボタンを押します(0<time<=20000と入力しても作動しないので注意)。
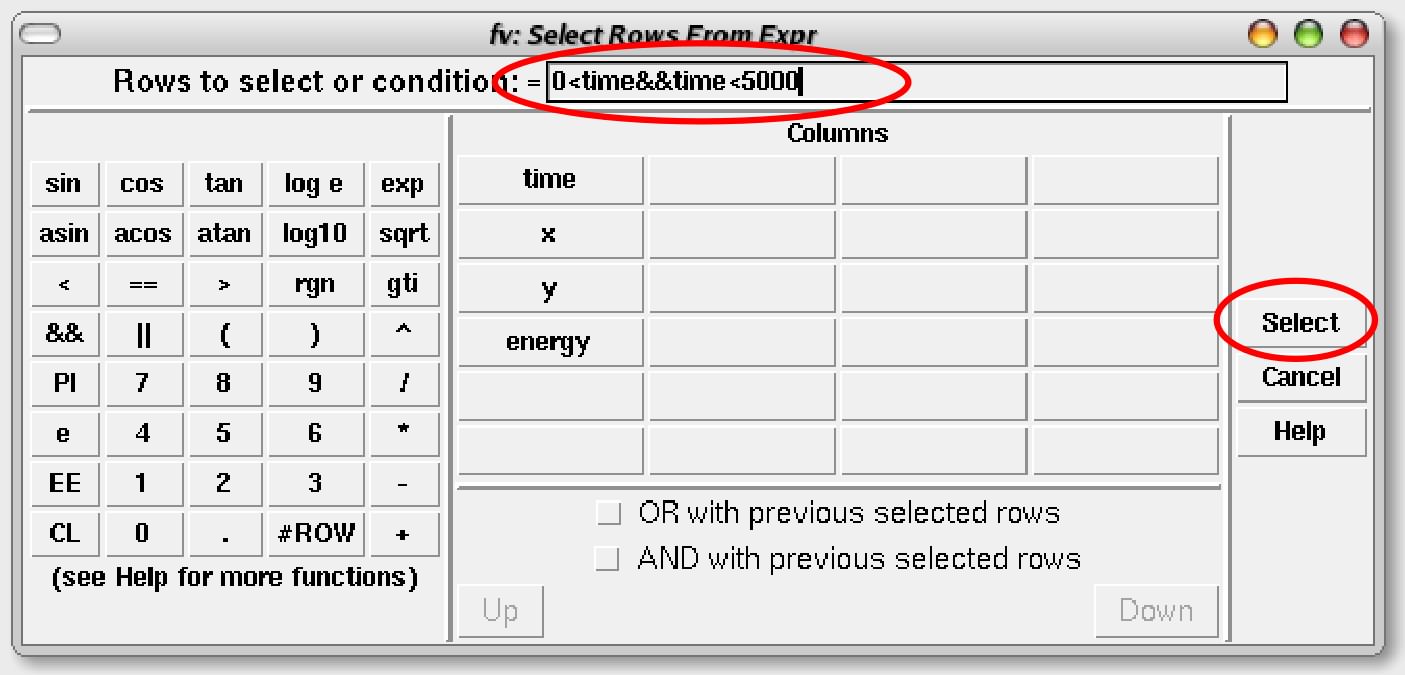
うまくいくと以下の図ように、選択された列のところが黄色になります。確認してください(この画面をスクロールして下に下げると黄色でない列が出てくることが分かります)。この列の1つ1つが CCD カメラに届いた光子1個1個の情報(到来時間、X座標の位置、Y座標の位置、光子のエネルギー)を表しています。

最後に選択された列(光子)だけをファイルに書き出しします。File→Export Hdu…と選択、「RhoOphCore_d1.fits」などと、わかりやすい名前を付けてSaveを選択します(拡張子は.fitsにしてください)。次にでてきた画面で、RowsをAllからSelectionに変えて、Saveを選択します。これで選ばれた、黄色で示された光子のみが書き出されます。
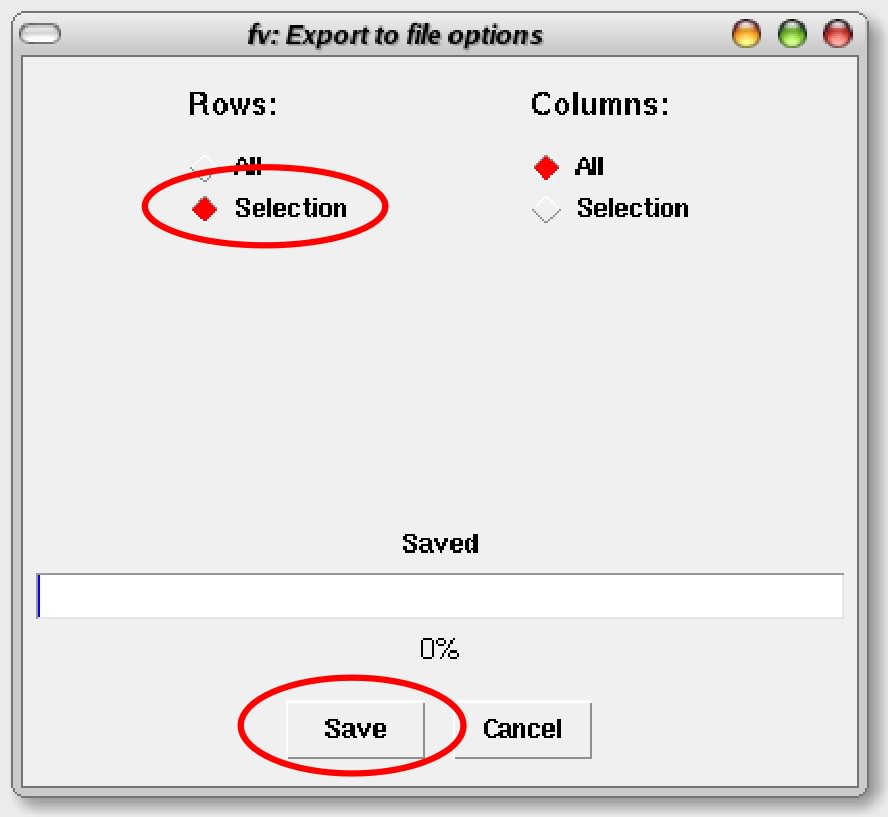
以下、timeの値を『20000<time&&time<=40000』と20000ずつずらしたものを保存していき、『60000<time&&time<=80000』、『80000<time』となるまで続けます。ここまでの作業が終わったらfvを終了します。
次に、ds9を起動させます。File→Open…を選択し、新しい面画が出たら、先ほど作成したファイルを順次開いていきます。ここでは、binをblock4に変更し、scaleをlogに変更します。これによりどのように画像が変化するのか自分の目で確認し、意味を考えてみましょう。次の時間帯のデータの開き方は、上部にあるFrameボタンを押して、New Frameを選択して画像の「枠」をまず確保し、File→Open…を選択します。これに対してもbinをblock4に変更します。
これらを繰り返してfvで作成した5つのファイルを全て開きます。最後にFrameボタンを押して、Blink Framesを選択します。これにより、開かれた画像が順次再生されムービーとして見ることができます。また、Blink Intervalではムービーの間隔を変更できます。画像の中心や拡大率を変えたい場合は、1つのファイルを位置をあわせて、上のFrameメニューから、Frame→Match Frame→WCS とすると、開いているすべての画像をそろえることができます。
Question 2.3. 動画は見られましたか? 動画からどんなことが分かりますか?
もし、時間があれば、5000秒ごとに20個のファイルを作って、動画を作成してみてください。
よりわかりやすくなります。このような形になります。
3. 中級編 〜 X線強度の変化を見てみよう
3.1. 1つの星を抽出したファイルを作ろう
2.3.で作った動画からは、たくさんの星の赤ちゃんがこの領域にあること、そしてそれぞれの赤ちゃんがさまざまに強度変動を起こしていることが分かったと思います。ここからは、とある一つの星に着目して理解をすすめていきましょう。ここでは、以下の画像の緑の四角の中にある光子だけを抽出して解析を進めていきます。

上の図から緑の四角は、XY座標の中心が(3845.5, 3309.5)、 幅が60です。
RhoOphCore.fitsを開いているfvのメニューから、Allをクリックします。すると、動画を作ったときと同様に数字が羅列された表がでてきます。
次に、表の上のメニューから、Edit→Select Rows…を選択し、面画が出たら、=の右側に、前回と同じように、 星の座標を入力します。ここでは、『3815.5<=x && x<=3875.5 && 3279.5<=y && y<=3339.5』 と入力し、Selectボタンを押します。
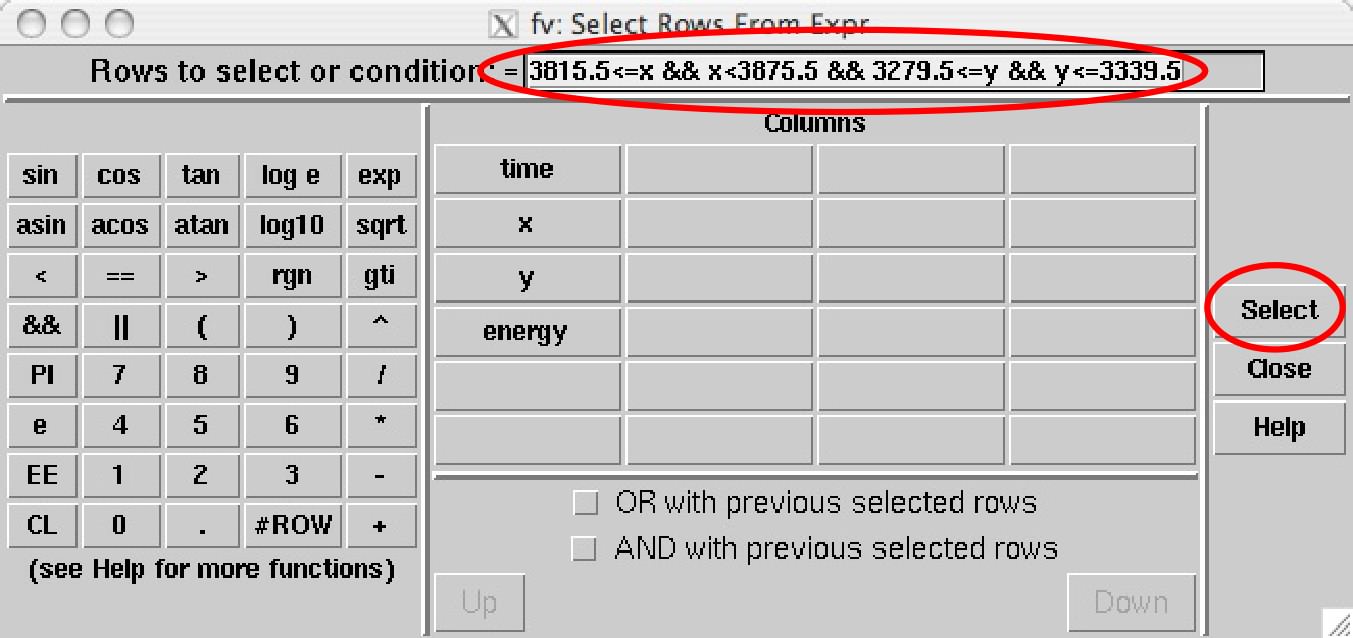
すると、以下のように表に、黄色い帯が表示されます。これらが 注目した星から来たX線の情報(光子)です。
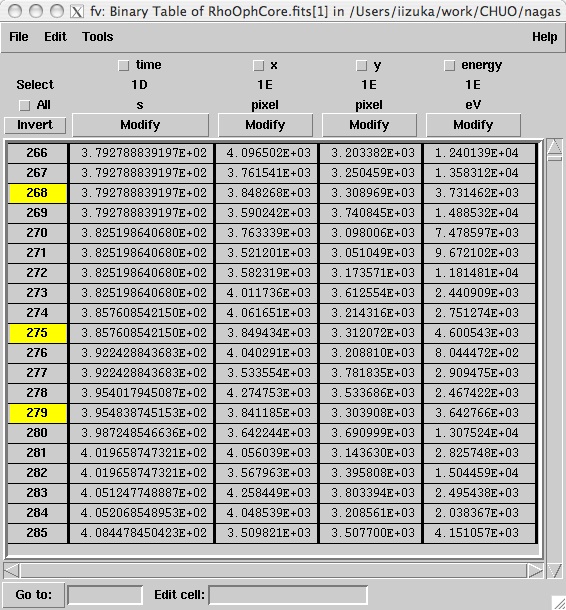
最後に、File→Export Hdu…と選択、名前(たとえば、RhoOphCore_s1.fits)を付けてSaveを選択します。
なお、先ほどと同じように、RowsをAllからSelectionに変えて、Saveすることを忘れないようにします。できたファイルをds9で確認をします。
Question 3.1 fvで作成したファイル(RhoOphCore_s1.fits)はds9で見るとどのようになっていますか?
3.2. X線の強度変化のグラフを作ろう
次に、2.3.で作った動画から分かった強度変動の様子をグラフにしてみましょう。注目した星のX線変動がどのようなものなのか、横軸が時間、縦軸がX線強度のグラフを作ってみます。このグラフの表示も fv でできます。一度 fv を終了します。そして再び、fv を起動させ、「Open File」を選んで、前回の3.1.作ったRhoOphCore_s1.fitsを開きます。

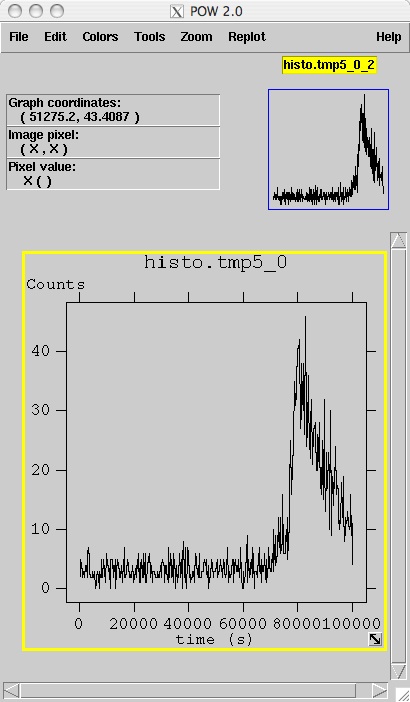
表示部分の「All」をクリックします。表がでてきたら、 表の上のメニューから、「Tools」→「Histgram...」を選び、 出てきた新しいwindowで、X=timeを選びましょう。Yは空欄のままにしましょう。 「Make」をクリックすると、横軸が時間、縦軸がX線強度の図、すなわち、X線の強度変動のグラフが出てきます。
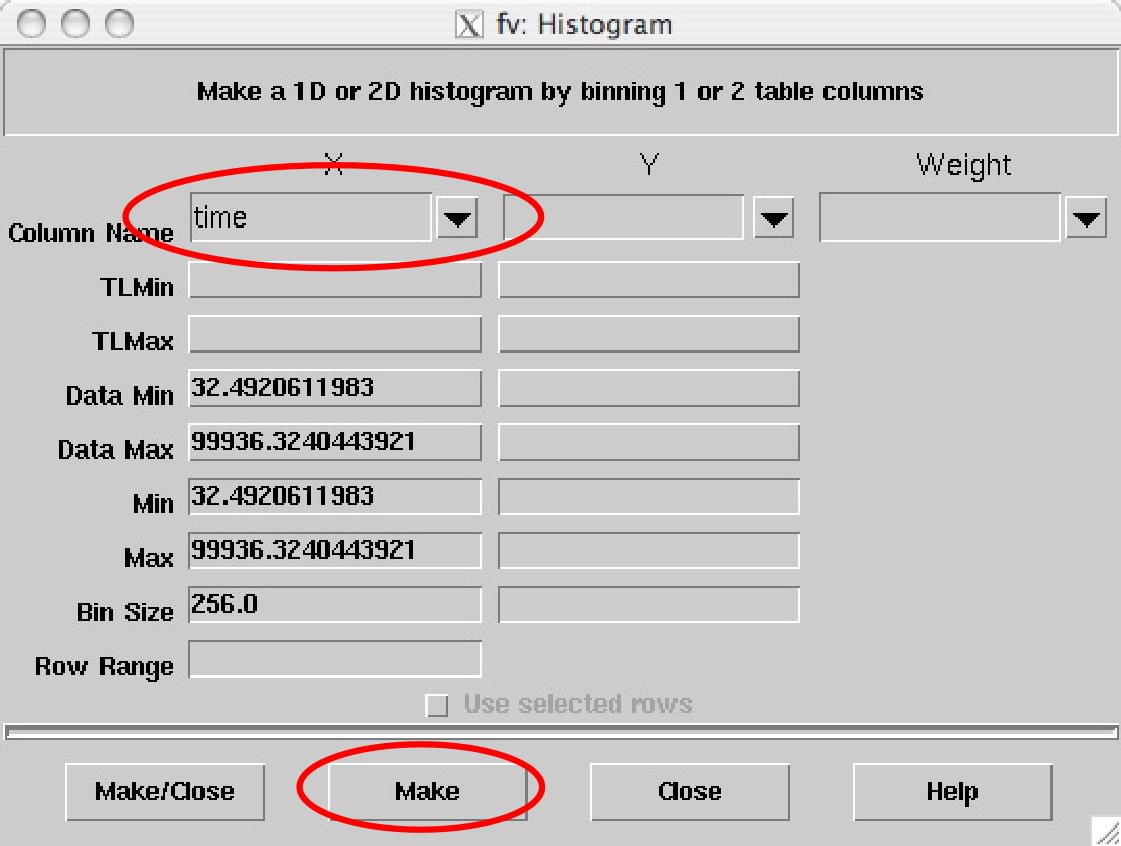
Question 3.2. X線の強度変化はどんな形をしていますか?
3.3 星の爆発現象「フレア」
前回3.2.の強度変動のグラフを見ると、X線強度が急激に高くなり、その後ゆるやかに低くなっていることが分かります。このような増光現象のことを一般的に「フレア」といいます。太陽においても「フレア」現象は見られます。
太陽におけるフレアは、太陽系内最大の爆発現象で、磁気嵐やオーロラ現象が発生したり、 地球近傍の衛星や無線通信に悪影響を与えることがしばしばあります。

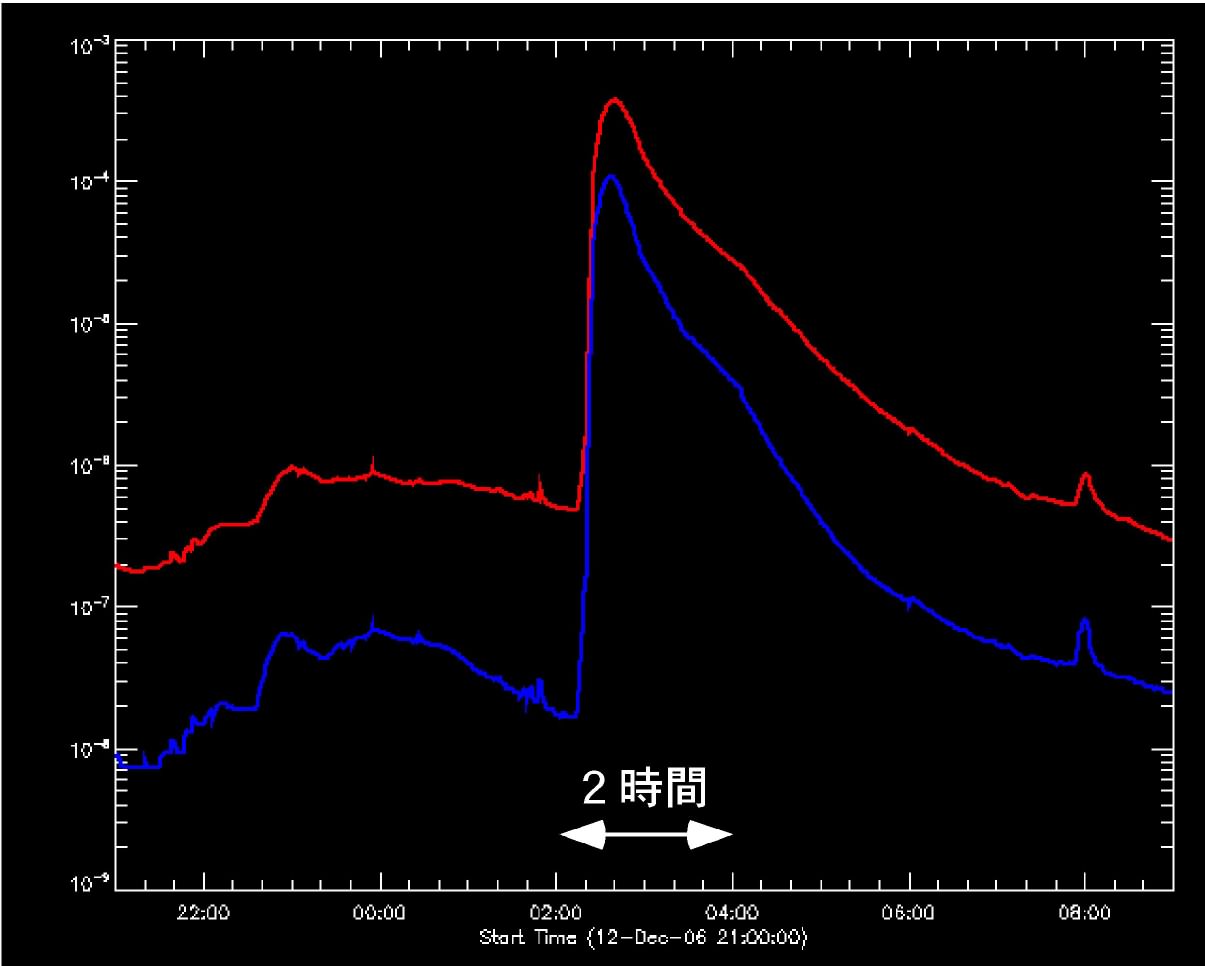
2006年12月13日、SOHO衛星がとらえた太陽フレア。左図がX線画像、右図はX線強度変動(国立天文台より)。
上の太陽のX線写真では特にループ状になった箇所が明るいことがわかります。ここには熱いプラズマが充満しており、そのプラズマからX線が放射されているのです。そして、このプラズマを爆発的に加熱する現象が太陽フレアなのです。太陽フレアは磁力線がつなぎかえられることによって、磁場のエネルギーが解放され、それが熱エネルギーに変換されて起きると考えられています。この熱いプラズマは放っておくと拡散してしまいますが、磁気ループの磁場に閉じ込められて形状が保たれています。太陽の詳しい説明については、「太陽表面の高エネルギー現象を探ろう」の教材を参考にしてください。太陽フレアが発生すると、X線やガンマ線から紫外線や可視光線、電波にいたるまでのさまざまな波長域で増光が見られます。
しかし、私たちがいま解析している星の赤ちゃんにおけるフレアは、そもそも太陽フレアと同種のものでしょうか。ここからは、今回注目した星のフレアが、どのような性質をもつのか、太陽フレアと違うのかを見ていきましょう。まずは、 3.2で出したX線強度変化のグラフから、上の太陽フレアの図のように、明るくなってから暗くなるまでどのくらいの時間がかかっているか、求めてみましょう。実際は、一番明るくなったところから、その半分の明るさになったところまでを見ます。
Question 3.3. 半分の明るさになるまでどのくらいの時間がかかっていますか?
4. 上級編 〜 吸収量、プラズマの温度、X線の明るさを出してみよう
4.1. X線の色「スペクトル」を作ってみよう
3.1.で抽出したデータ(RhoOphCore_s1.fits)を使って、注目した星のX線のスペクトルを作ってみましょう。スペクトルとは、どんなエネルギーのX線がどういう強度で来ているか、のグラフのことで、X線の色とも言えるものです。ここでも fv が使えます。前回に続いて、表の上のメニューから、Allをクリックします。そして、「Tools」→「Histgram...」を選び、 出てきた新しいwindowで、X=energyを選びましょう。Yは空欄のままにしましょう。
最小最大は適宜選ぶと見栄えのよいものができます。ここでは、最小値 Min=0 eV、最大値 Max=10000 eV、Bin Size=50 eVとします。「Make」をクリックすると、横軸がエネルギー、縦軸がX線強度の図、すなわち、スペクトルが出てきます。

Question 4.1. どんな形をしていますか? 特徴を述べてみてください。
4.2. フレアのところだけを抽出しよう
次に、フレアで増光した部分(これからは「フレアX線」と呼ぶことにします)だけのスペクトルを抽出するために、明るい時のスペクトルから暗い時のものを引き算しましょう。 3.2.で作ったX線強度変動を調べてみると、 明るい時は80000<time<100000 のデータが、暗い時は、たとえば40000<time<60000 のデータが使えます。下の解析の都合上同じ時間幅をとる必要があります。X線の色を4つの帯域にわけて、 暗い時と明るい時のそれぞれの光子数を調べていってください。なお、ここでは、4つの帯域を、 ①300-2000 eV、②2000-3000 eV、③3000-5000 eV、④5000-8000 eVに設定します。
| 色の幅 | 暗いとき | 明るいとき | 明るいとき−暗いとき | 割り算 |
|---|---|---|---|---|
| 帯域① 300 - 2000 eV |
--- | --- | --- | 帯域②÷帯域① |
| 帯域② 2000 - 3000 eV |
--- | --- | --- | |
| 帯域③ 3000 - 5000 eV |
--- | --- | --- | 帯域④÷帯域③ |
| 帯域④ 5000 - 8000 eV |
--- | --- | --- |
まずは、暗いときの帯域①の光子数です。 星のところだけを切り出したRhoOphCore_s1.fits を fv で開き、Allをクリックします。 表の上のメニューから、Edit→Select Rows…を選択し、面画が出たら、=の右側に、前回と同じように、 『40000<=time && time<=60000 && 300<=energy && energy<=2000』と 入力をします。そして「Select」を押して暗い時間帯の光子のみを抽出します。

続いて、表の上のメニューから、「Tools」→「Statistics...」を選ぶと 以下のような画面がでてきます。そこで、左から、「energy」を押すと、数字が表示されます。 このとき「Use selected rows」にチェックを入れるのを忘れないようにしてください。 この「Number of Values」を見ます。この「41」という数字が、 暗いとき(time=40000-60000)、帯域①(energy=300-2000 eV)のX線色のところの光子数になります。
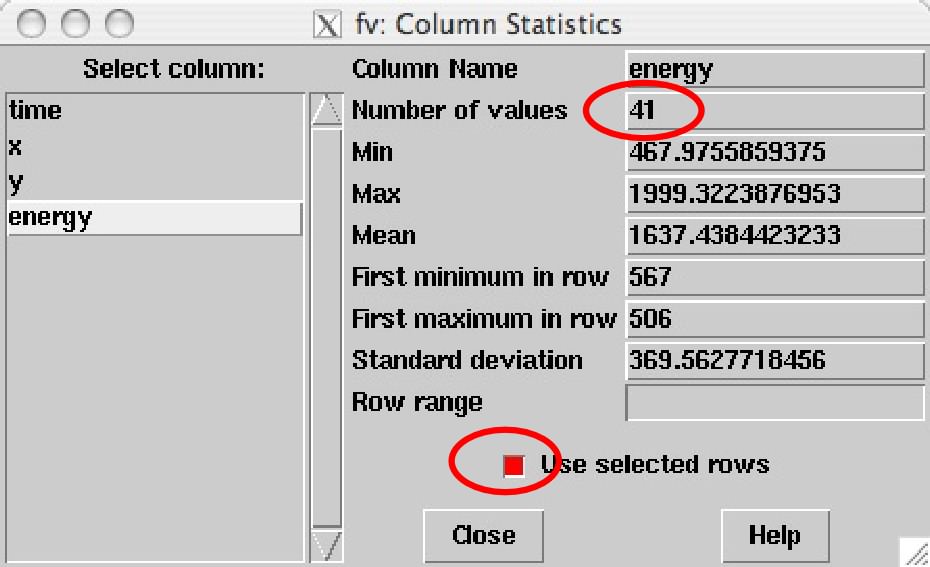
同様の方法で、
『40000<=time && time<=60000 && 2000<=energy && energy<=3000』
『40000<=time && time<=60000 && 3000<=energy && energy<=5000』
『40000<=time && time<=60000 && 5000<=energy && energy<=8000』
『80000<=time && time<=100000 && 300<=energy && energy<=2000』
『80000<=time && time<=100000 && 2000<=energy && energy<=3000』
『80000<=time && time<=100000 && 3000<=energy && energy<=5000』
『80000<=time && time<=100000 && 5000<=energy && energy<=8000』
についても行い、上の表をすべて埋めましょう。「引き算」の部分が「フレアX線」のスペクトルです。また、割り算についても行ってください。割り算が何を意味するかは、下の解析で分かります。
Question 4.2. 表はどのようになりましたか?
4.3. X線の吸収量を求めよう
吸収量とは、X線を放つ天体から人工衛星までの間に存在する物質によりX線が吸収される量のことです。単位はm-2 で表します。「長さが衛星から天体まで、断面積が1 m-2 の柱の中にある水素原子の数」で表すのです。柱密度とも呼ばれます。下図に模式図を示します。
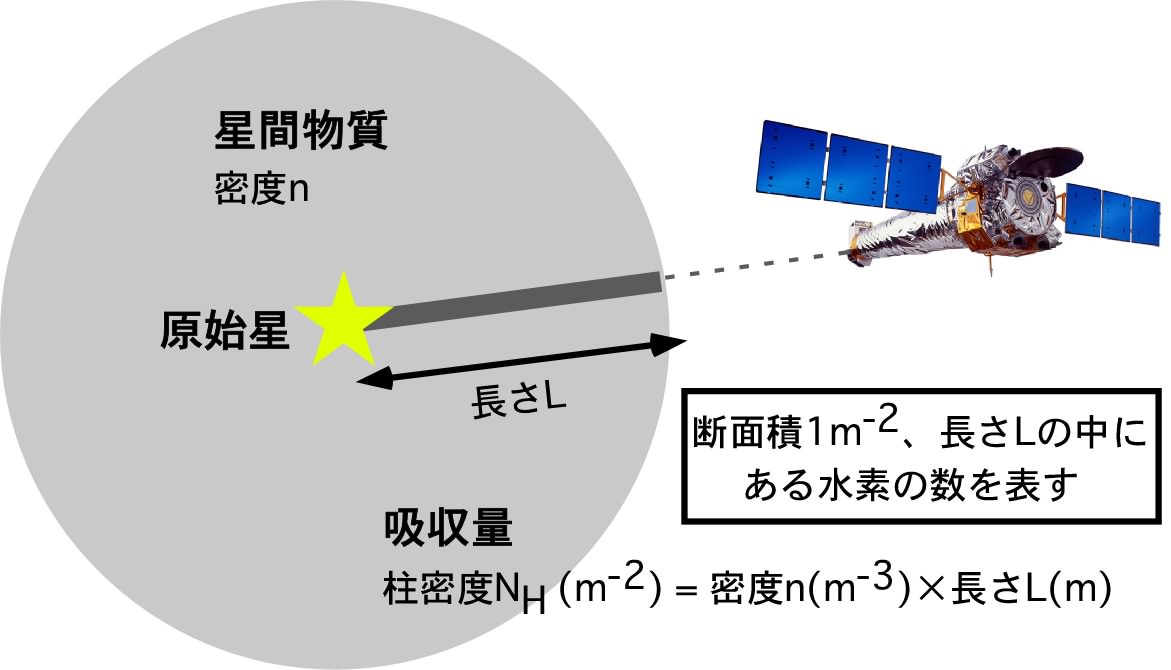
吸収量の模式図
たとえば、密度106 m-3 (1 cm-3)の星間物質が、銀河系程度の大きさ 10 キロパーセク(3万光年、3×1020 m)程度に広がっていると、銀河系のさしわたしの星間物質で吸収される量は柱密度にして

程度になります。吸収量が変わると、もともとのスペクトルが下図のように影響を受けます。主に、エネルギーの小さい帯域①のX線が吸収されることになります。
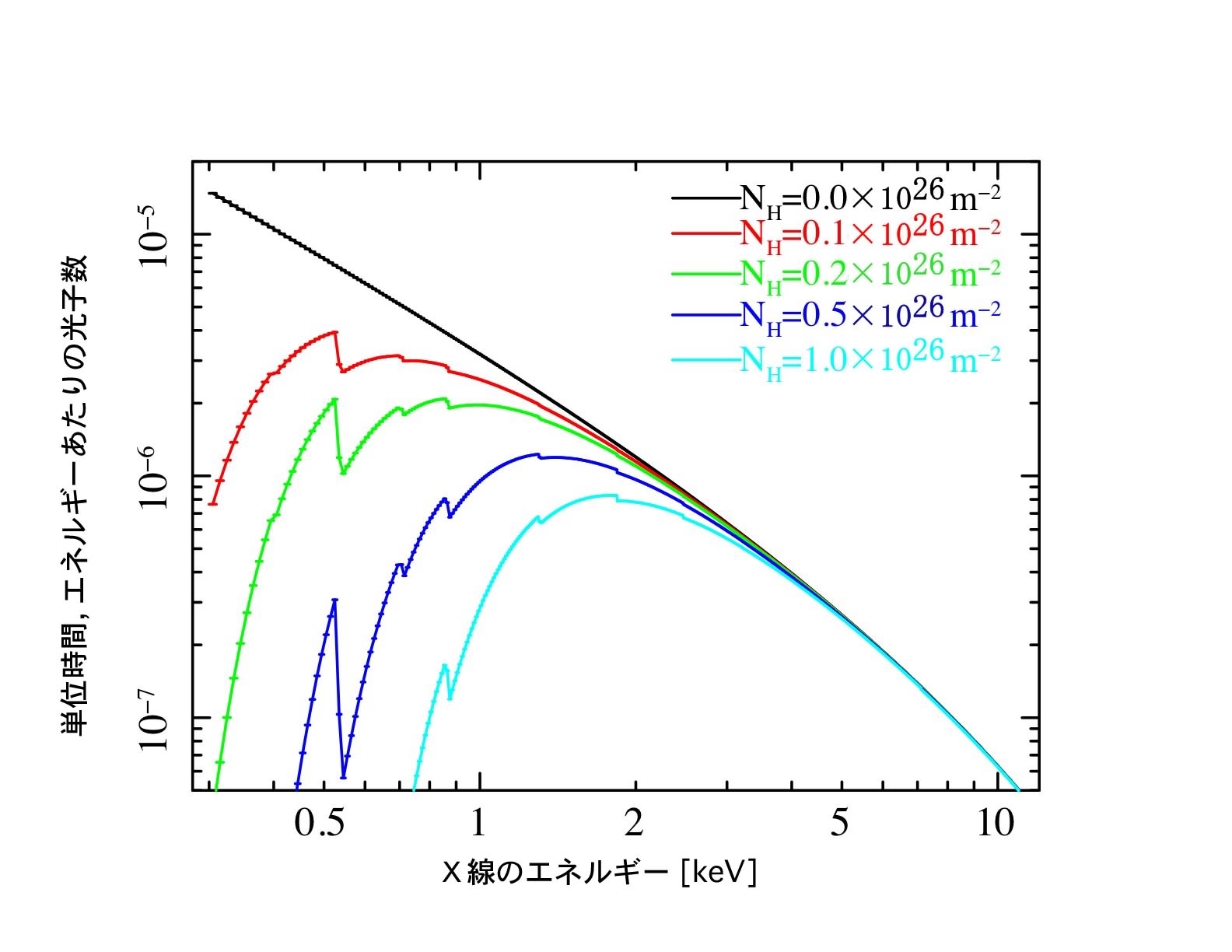
これは4.2で作った表の帯域②÷帯域①の値を使って、吸収量が求まることを意味します。下図に、帯域②÷帯域①の値と、吸収量の関係を示します。星の赤ちゃんが持つ、帯域②÷帯域①の値から縦軸の吸収量を読み取ってください。
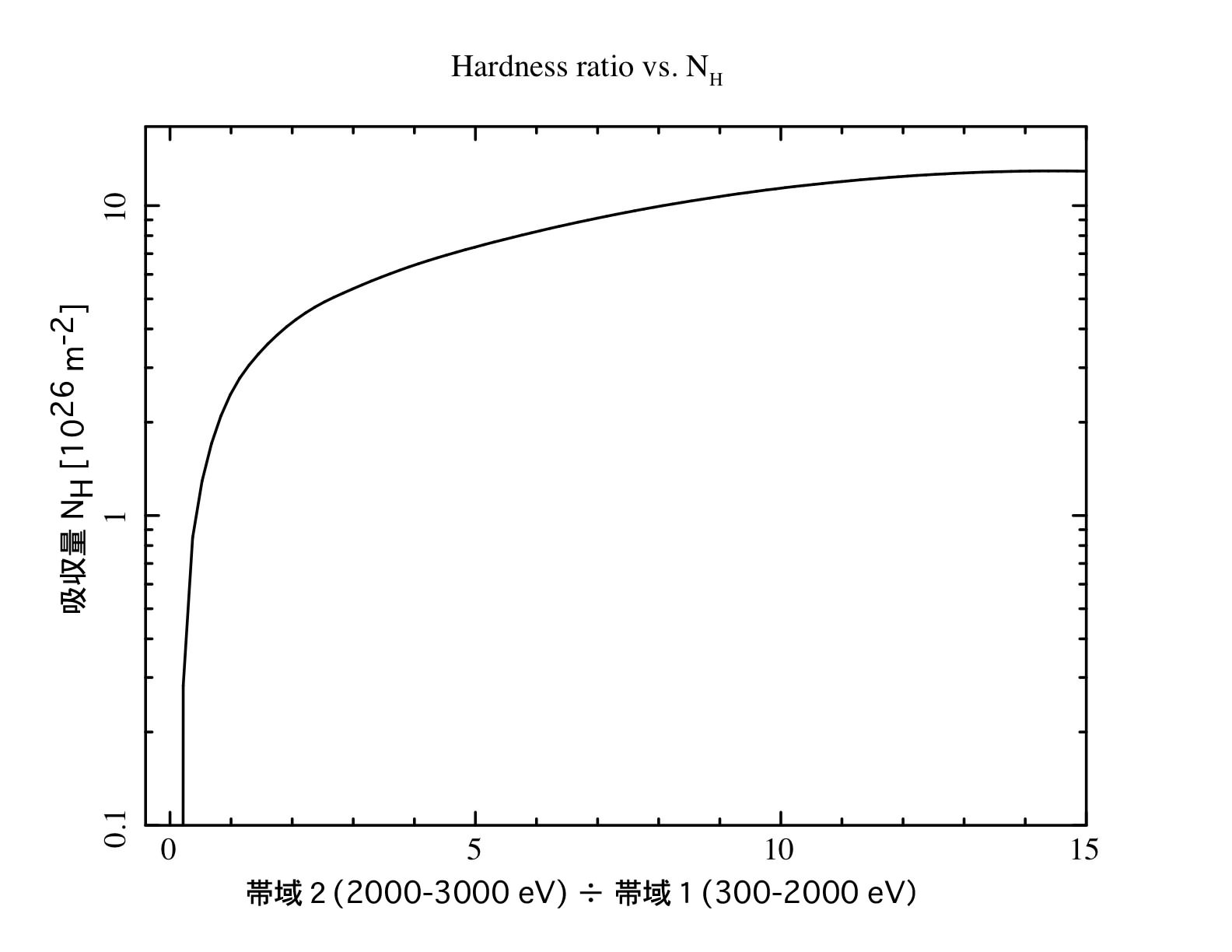
Question 4.3. 吸収量はいくつぐらいになりましたか?
上で求まった吸収量は、銀河系のさしわたしで吸収される量よりも大きい値です。しかし、へびつかい座暗黒星雲までの距離はたかだか145パーセク(473光年、4.47×1018 m)で、銀河系のさしわたしより2桁も小さいです。これは、暗黒星雲、ないしは星の赤ちゃんのごく近傍に吸収物質が集中して存在することを意味しています。星の赤ちゃんは、若ければ若いほどたくさんの塵やガスに包まれて存在します。今回X線で初めて確認できた星の赤ちゃんも本当に生まれたばかりであることが、この吸収量から分かります。
4.4. フレアを放つプラズマの温度を調べよう
次は、フレアを放つプラズマの温度を求めていきましょう。これもスペクトルの傾きから求めることができます。温度を変えるとどのようにスペクトルが変化するのかを下図に示します。
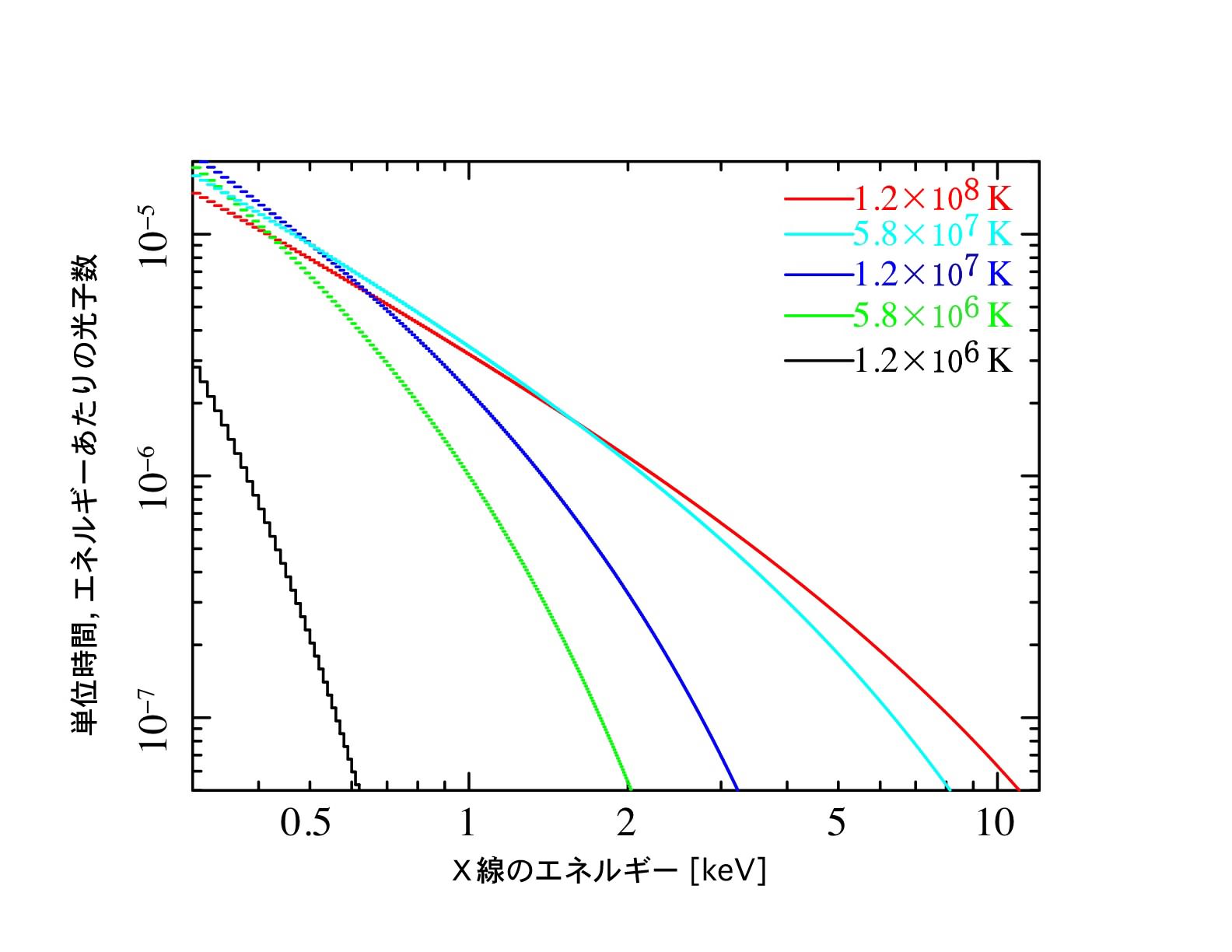
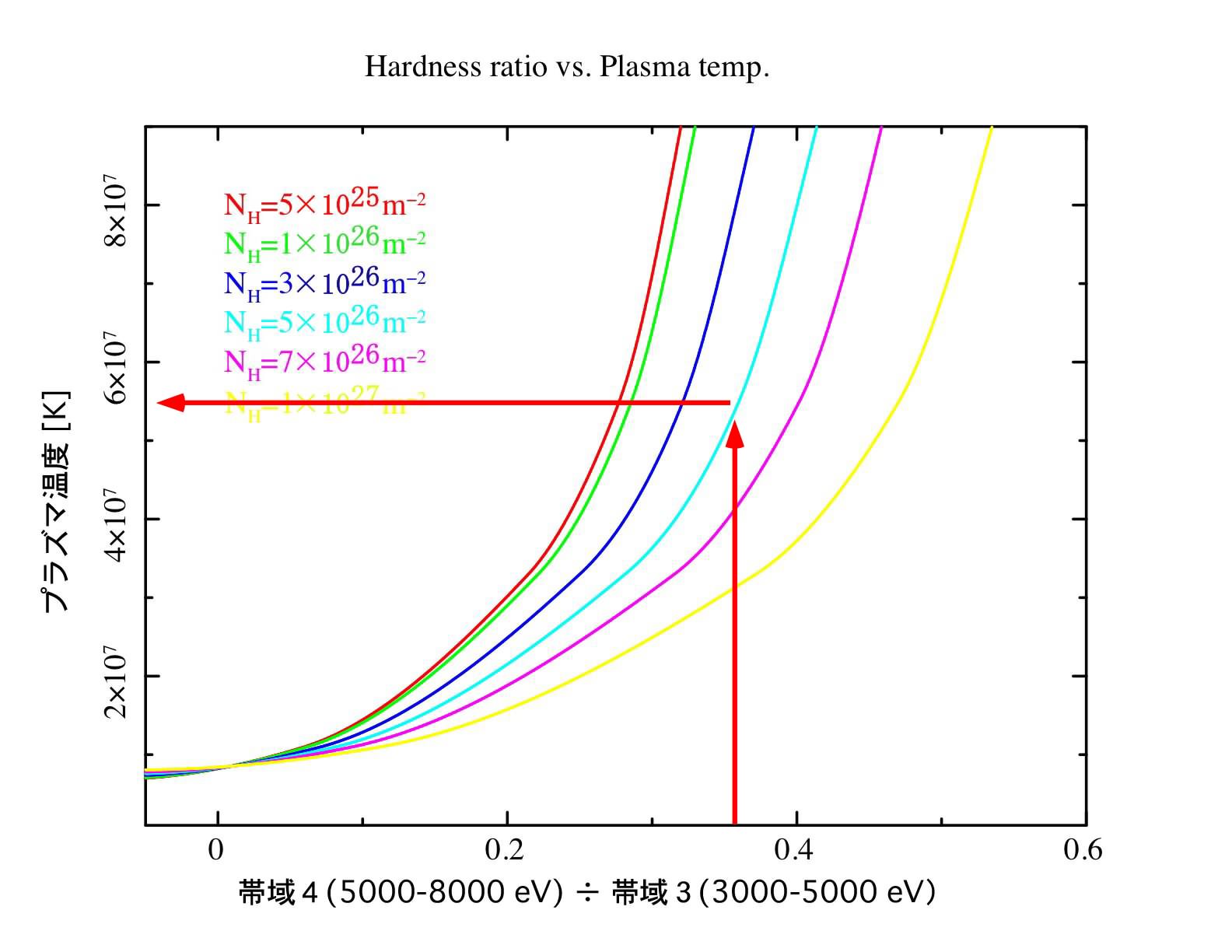
温度が高くなると、エネルギーの高い方までスペクトルがのびていることが分かります。これは上表の帯域④÷帯域③の比の値を使って、プラズマの温度が出せることを意味します。帯域④÷帯域③の値と、温度の関係を下図に示します。この比の値は、吸収量の値にも依存するので、様々な吸収量の値による、帯域④÷帯域③と温度の関係が示されています(ちなみに上で行った吸収量の見積りは、温度の値にはほとんど依存しません)。上で求めた吸収量の関係線を見つけて、帯域④÷帯域③の値に対応する縦軸の温度を読み取ってください。
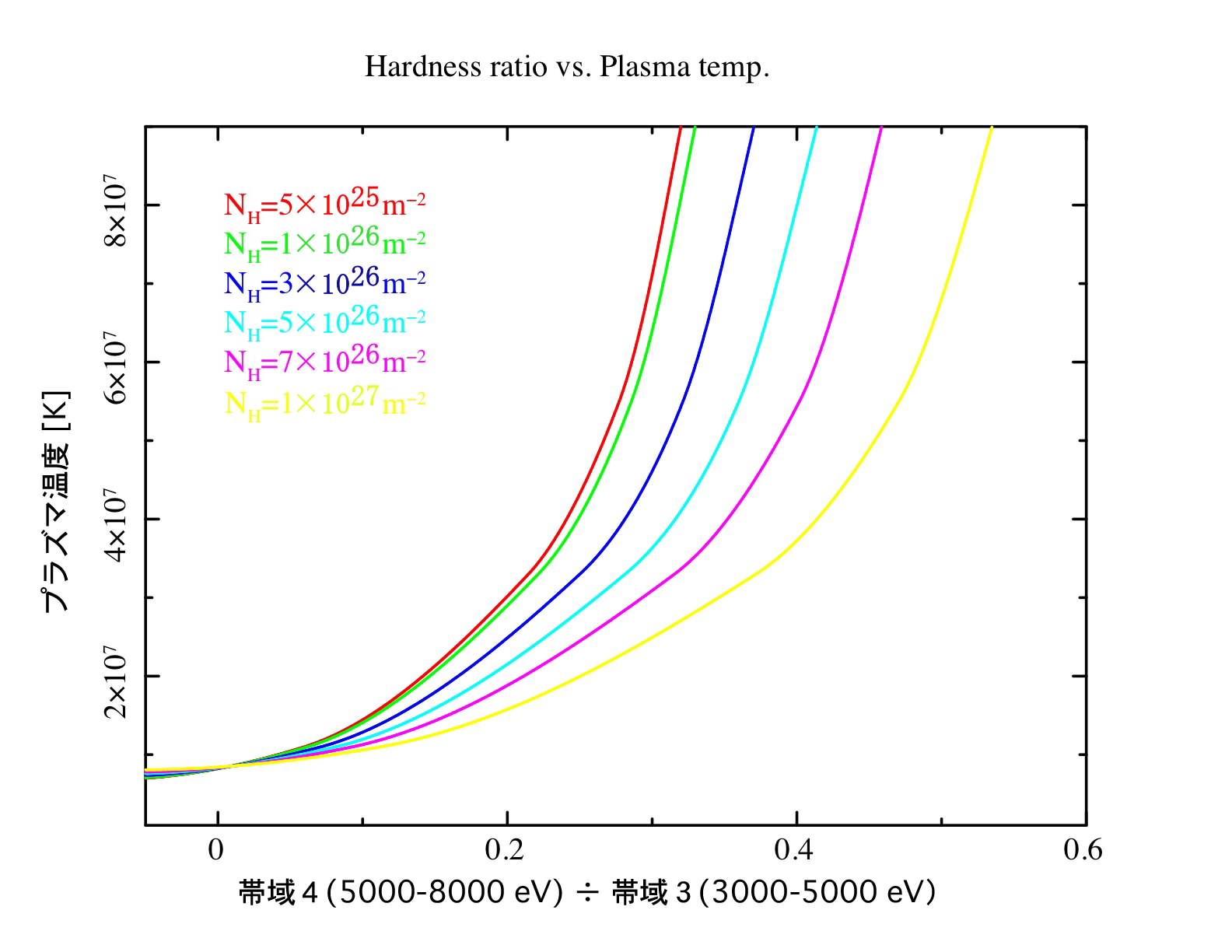
Question 4.4. 温度はどれだけになりましたか?
太陽フレアを放つプラズマの温度は、高くても2千万度程度なので、星の赤ちゃんでは数倍大きいことになります。星の赤ちゃんからのX線が検出される以前、原始星は高エネルギー現象とは無縁だと思われていました。原始星から観測されていたのは、星本体を囲むガスや塵で、その温度は20から30K程度の極低温だったからです。その極低温のど真ん中の星本体で、高いものでは1億Kを超す高エネルギー現象が起きていました。この事実は当時、非常な驚きを持って迎えられました。
4.5. フレアのX線光度を求めよう
最後に求めた吸収量と温度、および光子数から、フレアX線の光度を出しましょう。光度とは、天体が単位時間に放射するエネルギーのことです。そのため、フレア本来はどのくらい輝いているのか、吸収量を戻した形でスペクトルを積分する必要があります。ここでは 300 eV から 8000 eV の帯域での光度を求めましょう。
まず、4.2で求めた表におけるフレアX線の光子数(明るいときー暗いとき)を帯域①から④まで足し合わせましょう。同じようなスペクトル(吸収、温度)を持ち、既に光度が分かっている天体から実際に受かる光子数(これは吸収を受けています)と比較することにより、星の赤ちゃんの光度を求めることができます。下図に、いろいろな温度、吸収を持つ天体からどれだけの光子が受かるかを示します。この天体のX線光度は1023 W です(距離はへびつかい座ρ暗黒星雲までを仮定)。自分でもとめた温度と吸収量に近いところを見つけて、帯域すべての値を足し合わせた光子数と比較してください。その比がこの赤ちゃん星が出しているフレアX線の光度となります。
| 吸収量 [1026 m-2] | |||||||
|---|---|---|---|---|---|---|---|
| 0.5 | 1 | 3 | 5 | 7 | 10 | ||
| 温度 [107 K] |
1.2 | 470 | 240 | 57 | 27 | 17 | 10 |
3.5 |
480 | 330 | 150 | 100 | 76 | 55 | |
| 5.8 | 460 | 330 | 170 | 120 | 93 | 71 | |
| 8.1 | 440 | 330 | 176 | 127 | 100 | 78 | |
Question 4.5. フレアのX線光度はどれだけになりましたか?
5. 達人編 〜 太陽フレアと比較をしてみよう
5.1. 星の赤ちゃんのフレアの大きさ(体積)
さて、ここまででフレアを放つプラズマの温度、明るさを求めることができました。では、この赤ちゃん星のフレアX線はどのくらい大きいプラズマから放射されたものなのでしょうか?太陽フレアと比較してみましょう。フレアの大きさを出す方法は以下の式になります。

左辺は単位体積あたりの内部エネルギーです。そしてそれが放射冷却によって無くなっていくという仮定を右辺でしています。 n(密度)、k(ボルツマン定数)、T(温度)、Lx(X線光度)、t(暗くなる時間)、V(体積)です。知りたいのはV(体積)です。 分からないのは、n(密度)ですが、n(密度)は太陽と比較をするため、 太陽の値(n = 1016 m-3)を使うことにしましょう。まとめると以下のような表になります。
| 物理量 | 値 |
|---|---|
| 密度 n | 1016 m-3 |
| 温度 T | 4.4で見積もった値 |
| 暗くなる時間 t | 3.3で見積もった値 |
| X線光度 Lx | 4.5で見積もった値 |
| 体積 V | 求めたい値 |
さて、体積Vはいくつになりましたか? 上の式を使って計算してみましょう。 また、太陽フレアの温度は1×107 K、X線光度は1020 W として、太陽フレアの何倍になっているかも求めてみてください。なお、計算には、ボルツマン定数 k = 1.38×10-23 J/K = 1.38×10-23 W・s/K を用いてください。
Question 5.1. 大きさ(体積V)はどのくらいになりましたか? 太陽フレアの何倍になりましたか?
5.2. 星の赤ちゃんのフレアの大きさ(長さ)
上で求めたフレアの体積はなんと太陽本体の体積と同じくらいの大きさになっています。太陽本体の半径は7×108 m ですので、確かめてみましょう。また、4.5. で求めたフレアの光度が、太陽フレアの光度に比べ何桁も大きかったのは、この体積の違いが主であったことが分かったと思います。ところで、前にも述べましたが、太陽におけるフレアX線は、下図のように磁気ループによって閉じこめられたプラズマから放射されています。
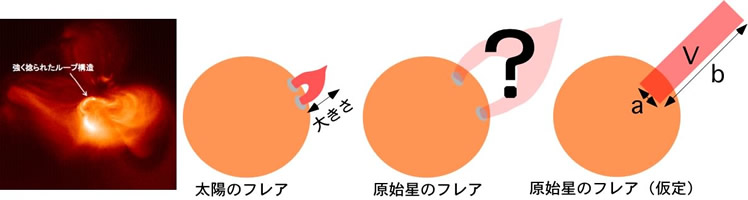
ひので衛星がとらえた太陽フレア直前のループ構造(左)と、太陽フレアと星の赤ちゃんのフレアの模式図
典型的な太陽フレアのループ形状は、断面の長さ(a)を1とすると、柱の長さ(b)が10です。星の赤ちゃんのフレアの形状も同様だと仮定すると、柱の長さ(b)はどのくらいになるでしょうか? 5.1.で求めた体積Vから、V=a×a×b、a:b=1:10として柱の長さ(b)を求めてみてください。
Question 5.2. 大きさ(長さb)はどのくらいになりましたか? 太陽半径の何倍になりましたか?
なんと太陽半径より1桁近く大きくなってしまいます!星を大きくまたぐフレアループが存在するのかも知れません。星の赤ちゃんでは、星へと降り積もる物質が円盤のようになっていることが、赤外線や電波の帯域で観測されています。この円盤から星本体へと磁気ループが繋がれていて星の赤ちゃんのフレアを引き起こす原因となっているとしたらどうでしょう。そして、この磁気ループが円盤から星本体へと物質を送り込む架け橋となっているとしたら、、、。これらはまだまだ私たちの想像の域を出ませんが、これから明らかにしていくべき重要な課題です。
5.3. 星の赤ちゃんのフレアの磁力
最後に赤ちゃんの磁力も出してみましょう。 高温プラズマが磁気ループに閉じ込められていると仮定すると下の式が成り立ちます。

この式の左辺はプラズマの圧力、右辺は磁気圧を表しています(真空の透磁率μ0 = 1.26×10-6 m kg s-2 A-2)。上と同様にn(密度)と、T(温度)を代入して、B(磁力)を求めてみてください。
Question 5.3. 磁力Bは太陽の何倍になりましたか?
星の赤ちゃんは若ければ若いほど、プラズマ温度が高い傾向があることがわかってきています。上の式から考えると、若ければ若いほど磁力が強くなるということになります。
6. 余力があれば ...
星の赤ちゃんでは、太陽フレアに似たフレアが起こっていたことが分かりました。
ただしその規模は何桁も大きいことが分かりました。星の赤ちゃんといってもなめたらあかんのです。
もし余力があれば以下のものにもチャレンジしてみてください。
・フレアをさらに時間分割してそれぞれの時間帯での温度を求めるとどうなるでしょうか? 「X線放射によって温度が下がり、それに伴ってX線光度も減衰する」という放射冷却の仮定が正しかどうかを確認してみてください。
・画像には、まだたくさんの星の赤ちゃんがあります。同様の手法で、他の星も解析してみてください。思わぬ発見があるかもしれません。
また、より理解をするためには以下の資料が参考になります。ぜひ読んでみてください。
・日本評論社 シリーズ現代の天文学6巻「星間物質と星形成」10.5章
・Kamata, Koyama, Tsuboi, and Yamauchi 1997, Publ. of the Astronomical Society of Japan 49巻 461-470頁
・Tsuboi et al. 1998, Astrophysical Journal v.503, p.894
・Tsuboi et al. 2000, Astrophysical Journal v.532, p.1089
・Montmerle, Grosso, Tsuboi, and Koyama 2000, Astrophysical Journal v.532, p.1097
・Imanishi, Koyama, and Tsuboi 2001, Astrophysical Journal v.557, p.747
・Mellinger 2009, The Publ. of the Astronomical Society of the Pacific, v.121, p.1180
答え
2.2
X線で星の赤ちゃんを見ると、たくさんの星が写っていることが分かりました。
全波長を通じて見ることができなかった、星の赤ちゃんの写真撮像に成功です!
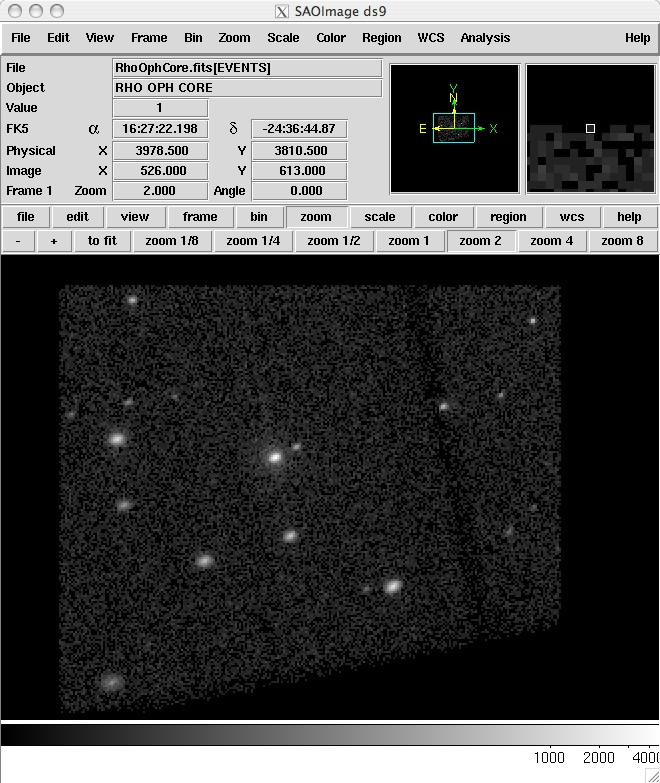
2.3
明るさがいろいろ変化している星がたくさんあることが分かります。
クリスマスツリーの様にちかちかと星の赤ちゃんが点滅していますね。
まるでイルミネーションのようです。
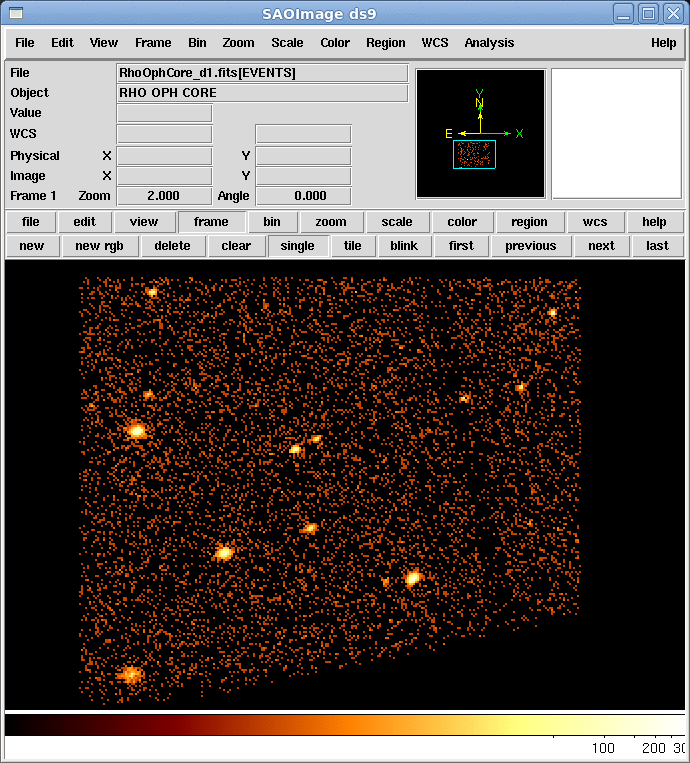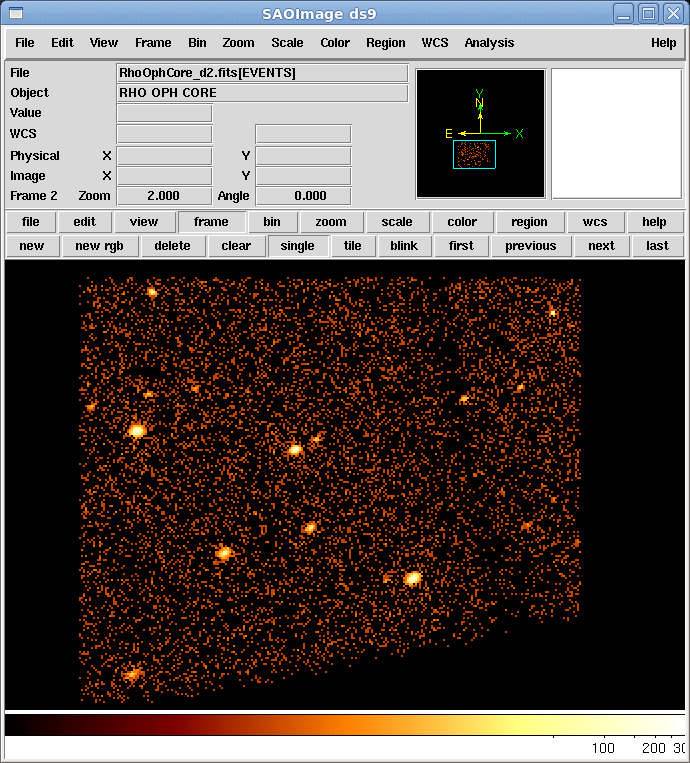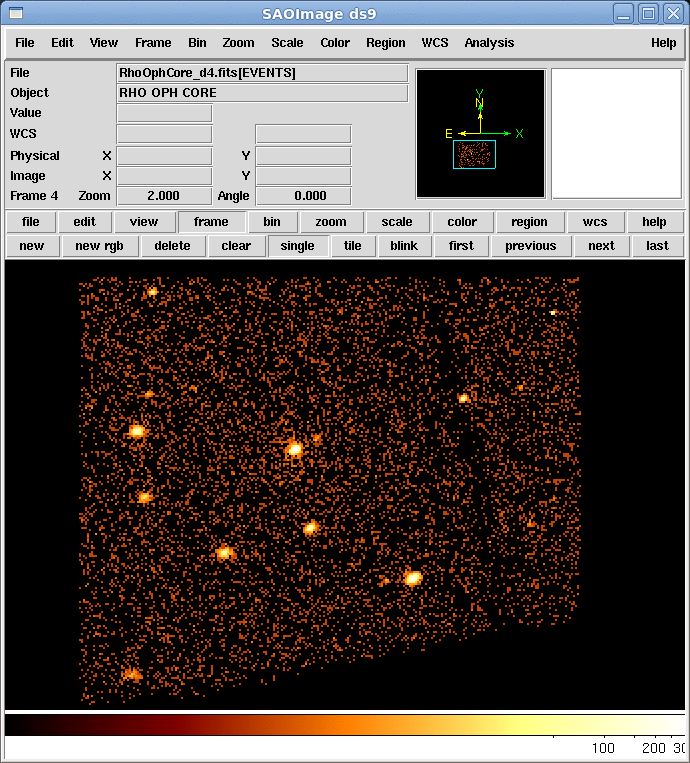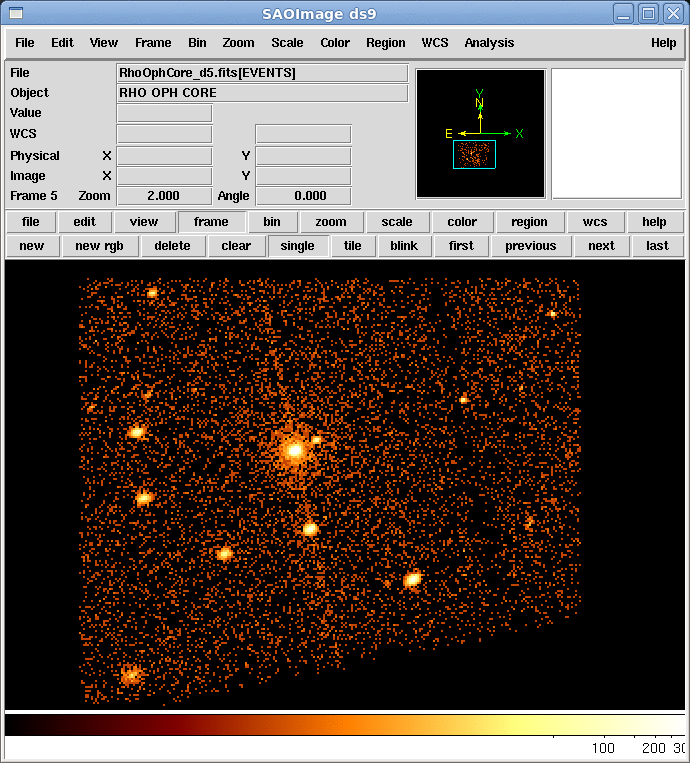
ちなみにファイルを5000秒ごとに20個作るとよりわかりやすくなります。
3.1
注目した星だけが表示されていればOKです。
3.2
急激に明るくなり、次第に暗くなっていることが分かります。「フレア」現象です。
星の赤ちゃんでは、なにやら激しいX線強度変動が起こっているようですね。
3.3
明るくなってから、暗くなる(実際は一番明るいところから半分になるところ)までは
10000秒程度です。数時間程度といったところでしょうか。
3.3の太陽におけるX線強度変動でも同じような時間になっていますね。
4.1
山なりになっていることが分かります。
この形状がどのようにして生まれるかは、4.3. および 4.4. 章で分かります。

4.2
こんな感じになればOKです。
| 色の幅 | 暗いとき | 明るいとき | 明るいとき−暗いとき | 割り算 |
|---|---|---|---|---|
| 300 - 2000 eV | 41 | 161 | 120 | 2.9 |
| 2000 - 3000 eV | 64 | 412 | 348 | |
| 3000 - 5000 eV | 74 | 760 | 686 | 0.35 |
| 5000 - 8000 eV | 29 | 272 | 243 |
4.3
こんな感じになればOKです。
吸収量NH = 5×1026 m-2 ぐらい

4.4
こんな感じになればOKです。
温度T = 5.8×107 K ぐらい
4.5
①から④をたし算すると、光子数は1400程度。
表から、吸収量NH = 5×1026 m-2、温度5.8×107 K の時、真のX線光度が1023 W になる光子数は、120程度。
よって、フレアのX線光度 Lx = 1.2×1024 W 程度。
太陽フレアのX線光度は、大きくて1020 W 程度です。なんと星の赤ちゃんで起こっているフレアの方が何桁も大きいのです!
5.1
こんな感じになればOKです。
体積V = 5.1×1026 m3。太陽フレアの2000倍程度。
5.2
こんな感じになればOKです。
長さb = 3.7×109 m。太陽半径の5倍程度。
5.3
こんな感じになればOKです。
磁力 B = 7.5×10-3 T 程度。
太陽フレアと温度が5倍違うので、磁力は太陽フレアの数倍程度。
単位換算
1W = 1×107 erg/s、1 erg = 1×10-7 J = 1×107 Ws
1 eV = 1.16×103 K、1 keV = 1.16×106 K
1 eV= 1.60×10-12 erg、1 K = 1.38×10-23 J = 1.38×10-23 Ws
1 gauss = 10-4 T (テスラ)
1 cm = 10-2 m
1 cm2 =10-4 m2、1 cm3 =10-6 m3
1 cm-2 = 104 m-2、1cm-3 = 106 m-3
1 pc = 3.26 光年 = 3.08×1016 m
1 kpc = 3.26×103 光年 = 3.08×1019 m
文責
坪井陽子、飯塚亮、菅原泰晴、他大学院生(中央大学 理工学部物理学科 宇宙物理学研究室)2010.01.21