Next: 中性子星、白色矮星の表面温度
Up: 大雑把に天体の物理量を求める事
Previous: 黒体輻射の例
Contents
黒体輻射をしている物体の表面から、単位面積あたり放射されるエネルギーを求めよう。
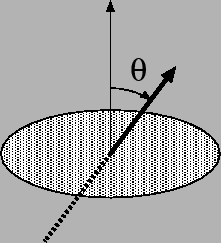
黒体輻射の式に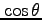 を掛けて(ここに注意!)、全振動数と、立体角で
を掛けて(ここに注意!)、全振動数と、立体角で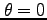 から
から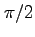 まで積分する。
立体角で積分する部分は
まで積分する。
立体角で積分する部分は
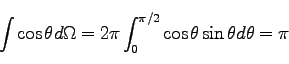 |
(259) |
となる。よって、求めるフラックスは
| |
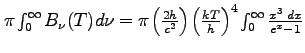 |
|
(260) |
| |
![$\textstyle = \frac{2\pi^5k^4}{15 c^2 h^3}T^4 \equiv \sigma T^4 \;\;[{\rm erg/s/cm^2}].$](img816.png) |
|
(261) |
ここで、
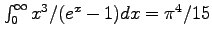 を用いた。
を用いた。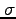 が
ステファンボルツマン定数であり、以下の値を持つ。
が
ステファンボルツマン定数であり、以下の値を持つ。
![\begin{displaymath}
\sigma=5.67 \times 10^{-5}\; [{\rm erg/s/cm^2/K^4}] = 1.03 \times 10^{24} \; [{\rm erg/s/cm^2/keV^4}].
\end{displaymath}](img818.png) |
(262) |
Ken EBISAWA
2011-05-30
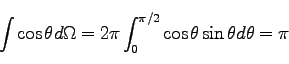
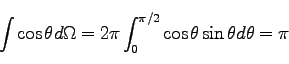
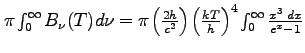
![]() を用いた。
を用いた。![]() が
ステファンボルツマン定数であり、以下の値を持つ。
が
ステファンボルツマン定数であり、以下の値を持つ。