ポアソン分布

図11の光度曲線（ライトカーブ）は、実際のX線衛星データから取ってきたものである。

Figure: 暗いX線天体を1ビン1秒で、100秒観測したときの光度曲線。 横軸は時間、縦軸は、1ビンあたりのX線光子数。平均値0.55に横線を引いた。

暗い天体を観測し、一秒ごとに、X線検出器に 入射するX線の数を、100秒の間、カウントした。その値を書き下してみると、以下の通りである。

0 0 2 0 1 0 0 0 0 0 0 0 0 1 0 4 0 1 1 1 1 0 1 1 0 0 1 0 0 0 1 0 0 0 1 0 0 1 0 0 4 0 1 0 0 0 0 0 1 1 1 2 0 0 0 2 1 1 1 2 1 0 0 0 1 0 1 1 2 0 1 1 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 2 0 0 0 1 0 0 2 0 2 0 1 0

全部で100ビンのうち、0カウントのビンが59、1カウントが31ビン、2カウントが8ビン、3カウントが0ビン、4カウントが 2ビンあることがわかるだろう。これを、1ビンに光子が0, 1, 2, 3, 4カウント 入る確率は、それぞれ、0.59, 0.31, 0.08, 0, 0.02 と考えても良い。 そのヒストグラムは、図12の通り。また、平均値は、 $(1 \times 31 + 2 \times 8 + 4 \times 2 )/100=0.55$ である。

図12で赤丸で示したのは、以下の式で、$\mu=0.55$のときに、 $i=0,1,2,3,4,5,,$ に対応する点である。

$$P_P(i; \mu) = \frac{\mu^i}{i!} e^{-\mu}$$ (231)

この式が、平均$\mu$のポアソン分布に他ならない（$\mu$は実数であるが、 $i$は整数値、$0,1,2,3,,$の場合にのみポアソン分布が定義されている事に注意せよ）。ポアソン分布の具体的解釈の一つの例として、 検出装置の1ビンに平均$\mu$個の割合で光子が入射してくる場合を考える。統計的な揺らぎにより、 実際に1ビンあたりに検出される光子の数は、$\mu$のまわりでばらつく。 実際に検出される光子数が$i=0,1,2,3,,,$ である確率が、(231) で与えられる。この状況が 図12、図14で示されている訳である。 「天体を観測したとき、1時間ビンあたりに落ちる光子数の分布はポアソン分布に従う」 ことを覚えておこう。

式(231)は暗記してしまうと良い。 思い出すために手がかりと成るのは、平均$\mu$のとき、1ビンに全く光子が入らない確率は、 $e^{-\mu}$ということである。

Figure: 観測されたX線データのヒストグラム（黒）と平均0.55のポアソン分布（赤）。

当然であるが、平均$\mu$の値によらず、1ビンに入る光子数$i$が0,1,2,3,,,である確率をすべて足すと1になることに注意しよう。

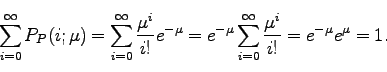$$\sum_{i=0}^{\infty} P_P(i; \mu) = \sum_{i=0}^{\infty}\frac{\... ...u} \sum_{i=0}^{\infty}\frac{\mu^i}{i!} = e^{-\mu} e^{\mu} =1.$$ (232)

また、すでに「式(231)の分布の平均は$\mu$」、と言ってしまっている訳だが、平均 (mean)の定義から その値が$\mu$になることを確認しておこう。

$$Mean \equiv \sum_{i=0}^{\infty} i\; P_P(i; \mu) =\sum_{i=i}^... ...} \mu \sum_{i-1=0}^{\infty} \; \frac{\mu^{i-1}}{(i-1)!}$$

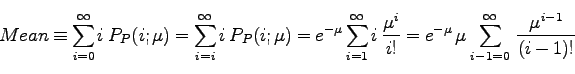
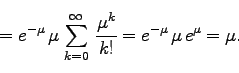$$= e^{-\mu} \mu \sum_{k=0}^{\infty} \; \frac{\mu^{k}}{k!} = e^{-\mu} \mu e^{\mu} = \mu.$$ (233)

さて、一般の確率分布関数で、平均の回りにその分布がどれだけばらついているか、を 分散(Variance) で表す。分散が大きいほど、ばらつきが大きい。 各ビンに入る光子数$i$と 平均の光子数$\mu$について、$(i-\mu)^2$をすべての$i$について平均したものが分散になる。

$$Variance \equiv \sum_{i=0}^{\infty} (i-\mu)^2\; P_P(i; \mu) =\sum_{i=0}^{\infty} (i^2- 2i \mu + \mu^2)\; P_P(i; \mu)$$

$$=\sum_{i=0}^{\infty} i^2P_P(i; \mu) - 2 \mu \sum_{i=0}^{\inf... ...infty} P_P(i; \mu) =\sum_{i=0}^{\infty} i^2P_P(i; \mu) - \mu^2$$

$$=\sum_{i=0}^{\infty} i^2\; \frac{\mu^i}{i!}\;e^{-\mu} - \mu^... ...-1=0}^{\infty} i \; \frac{\mu^{i-1}}{(i-1)!}\;e^{-\mu} - \mu^2$$

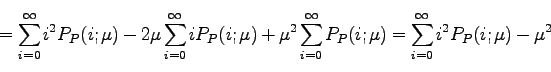
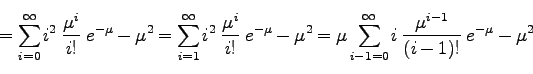
$$= \mu \sum_{k=0}^{\infty} (k+1) \; \frac{\mu^{k}}{k!}\;e^{-\mu} - \mu^2 = \mu (\mu + 1) - \mu^2 = \mu.$$ (234)

導出はちょっとやっかいだったが、ここで得られたとても大切な事実、「ポアソン分布の分散は平均に 等しい」ということは暗記しておこう。