 |
1981年に初めて活動銀河(クェーサー)の電波観測から超光速運動を報告した論文 ("Superluminal expansion of quasar 3C273", Pearson et al. Nature, 1981, 290, 365)のアブストラクトはわずか一行、以下の通りである: ``Maps of the radio structure of 3C273 show directly that it expanded with an apparent velocity 10 times the speed of light from mid-1977 to at least mid-1980.''
活動銀河が電波を放出すること、しばしばそれがジェットのように中心天体から吹き出すように 見えることはすでに知られていたが、それが中心天体から離れていく速度が光速を10倍以上も超えているように見えることが発見されたのである。これをどのように解釈したら良いだろうか?
 |
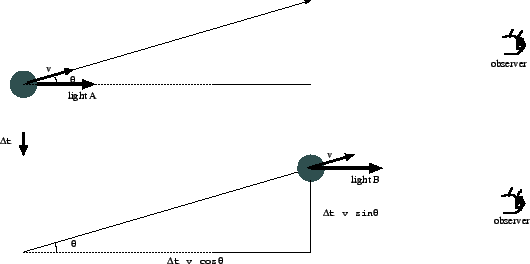
図6.2で、上図がブラックホールからジェットが放出された瞬間(速度![]() 、観測者に対する
角度
、観測者に対する
角度![]() )、下図がそれから
)、下図がそれから![]() 経過したところである。前者の時刻に放出された光をlight A、後者の時刻に放出された光をlight Bとしよう。天体から観測者までの距離を
経過したところである。前者の時刻に放出された光をlight A、後者の時刻に放出された光をlight Bとしよう。天体から観測者までの距離を![]() とすると、観測者がlight Aを受け取る時刻は、light Aが発せられてから
とすると、観測者がlight Aを受け取る時刻は、light Aが発せられてから![]() 後である。一方、light Bを受け取るのは、
後である。一方、light Bを受け取るのは、
![]() 後である。よって、観測者がlight Aを受けてからlight Bを受けるまでの経過時間は、
後である。よって、観測者がlight Aを受けてからlight Bを受けるまでの経過時間は、
![]() となる。また、観測者にとっては、ジェットが視線方向と垂直に
となる。また、観測者にとっては、ジェットが視線方向と垂直に
![]() だけ移動したように見える。よって、視線方向と垂直の見かけの速度は、
だけ移動したように見える。よって、視線方向と垂直の見かけの速度は、
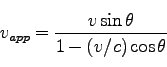 |
(112) |
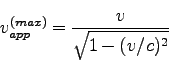 |
(113) |