



Next: 四元数と回転
Up: 四元数と座標変換、人工衛星の姿勢
Previous: 四元数(quaternion)
Contents
四元数は19世紀にハミルトンによって発見されたそうだ。数学的な側面はともかく、ここでは四元数の
応用面について述べる。すぐ後に述べるように、ノルム(norm)が1である単位四元数 (unit quarternion)は、3次元直交座標系の間の
直交変換を記述する。
四元数は複素数の拡張として、以下のように定義される。
 |
(71) |
ここで、 は実数である。
は実数である。
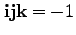 の左から
の左から を掛けて
を掛けて
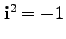 を使うと、
を使うと、
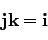 |
(72) |
が得られる。
同様に、右から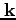 を掛けて
を掛けて
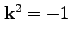 を使うと、
を使うと、
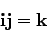 |
(73) |
が得られる。式(72)の左から式(73)を掛けて
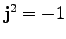 を使うと、
を使うと、
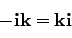 |
(74) |
が得られる。
同様に、(72)の右から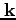 を掛けて、
を掛けて、
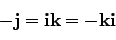 |
(75) |
が得られる。左から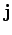 を掛けると、
を掛けると、
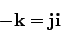 |
(76) |
が得られる。最後に、
(73)の右から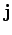 を掛けて、
を掛けて、
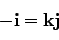 |
(77) |
が得られる。以上をまとめて、使いやすい形として、
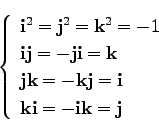 |
(78) |
を得る。
また四元数を以下のようにも表す。
![\begin{displaymath}
q = [{\bf v}, w]
= [(x,y,z), w]
= [x,y,z, w].
\end{displaymath}](img232.png) |
(79) |
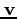 は、3次元空間のベクトルを表す。
は、3次元空間のベクトルを表す。
![$q = [{\bf v}, w], q'= [{\bf v'}, w']$](img234.png) とするとき、四元数同士の和は四元数であり、それは次のように定義される。
とするとき、四元数同士の和は四元数であり、それは次のように定義される。
![\begin{displaymath}
q + q' = [{\bf v}, w] + [{\bf v'}, w']
\equiv [{\bf v}+{\bf v'}, w + w'].
\end{displaymath}](img235.png) |
(80) |
積については、以下のように考えられる。
ここで、式の変形には、(78)を用いた。
四元数の積が可換でないことに注意(異なる軸の周りの回転が可換でないことに対応している)。また、
![$q'' = [{\bf v''}, w'']$](img244.png) としたとき、
としたとき、
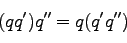 |
(86) |
が成立する![[*]](file:/usr/local/share/lib/latex2html/icons/footnote.png) 。
。
定数や3次元ベクトルも、四元数表示することができる。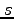 を実数の定数としたとき、その四元数表示は、
を実数の定数としたとき、その四元数表示は、
![$[0,0,0,s]=[{\bf0}, s]$](img249.png) 。
。
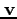 を3次元ベクトルとしたとき、その四元数表示は、
を3次元ベクトルとしたとき、その四元数表示は、![$[{\bf v}, 0]$](img251.png) 。定数や3次元ベクトルを四元数表示したとき、それらを
含む四元数の積に関して、以下は自明である。
。定数や3次元ベクトルを四元数表示したとき、それらを
含む四元数の積に関して、以下は自明である。
![\begin{displaymath}
s q = [{\bf0}, s][{\bf v}, w] = [s {\bf v}, sw] = qs,
\end{displaymath}](img252.png) |
(87) |
![\begin{displaymath}
{\bf v} {\bf v'} = [{\bf v}, 0][{\bf v'}, 0] = [{\bf v}\times{\bf v'}, -{\bf v}\cdot{\bf v'}].
\end{displaymath}](img253.png) |
(88) |
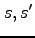 を四元数の定数、
を四元数の定数、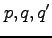 を任意の四元数としたとき、以下のように線型性が成立する。
を任意の四元数としたとき、以下のように線型性が成立する。
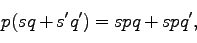 |
(89) |
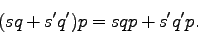 |
(90) |
四元数の共役(conjugate)の定義と、その性質は以下の通りである。
![\begin{displaymath}
q^\ast = [{\bf v},w]^\ast \equiv [-{\bf v},w].
\end{displaymath}](img258.png) |
(91) |
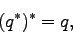 |
(92) |
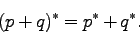 |
(94) |
ノルムの定義と性質は以下の通りである。
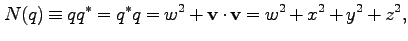 |
|
|
(95) |
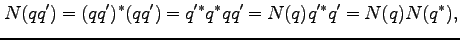 |
|
|
(96) |
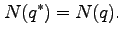 |
|
|
(97) |
特に、ノルムが1である四元数を単位四元数(unit quaternion)と呼ぶ。
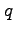 の逆四元数を
の逆四元数を
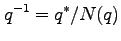 |
|
|
(98) |
で定義する。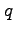 が単位四元数であるとき、
が単位四元数であるとき、
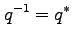 |
|
|
(99) |
である。




Next: 四元数と回転
Up: 四元数と座標変換、人工衛星の姿勢
Previous: 四元数(quaternion)
Contents
Ken EBISAWA
2011-05-30
![]() の左から
の左から![]() を掛けて
を掛けて
![]() を使うと、
を使うと、
![]() としたとき、
としたとき、
![]() を実数の定数としたとき、その四元数表示は、
を実数の定数としたとき、その四元数表示は、
![]() 。
。
![]() を3次元ベクトルとしたとき、その四元数表示は、
を3次元ベクトルとしたとき、その四元数表示は、![]() 。定数や3次元ベクトルを四元数表示したとき、それらを
含む四元数の積に関して、以下は自明である。
。定数や3次元ベクトルを四元数表示したとき、それらを
含む四元数の積に関して、以下は自明である。