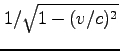特殊相対性理論が必要になる場合

ここでは直交変換の応用として、特殊相対性理論について学んでみよう。 等速運動する二つの座標系(慣性系)の どちらでも物理法則が全く同じように記述できる、というのが特殊相対性原理である(この宇宙に特別な慣性系は存在しない)。光速はどちらの座標系でも同じ値を取るし、どちらの系からも相手の系が同じように見える。 その間の座標変換はローレンツ変換で与えられ、以下に示すように、それは四次元時空における直交変換と考えても良い。しかし、ほとんどの場合、力学の問題を解くときに、私たちはローレンツ変換や相対論的力学を知らなくても良い。それは何故だろうか？その答えは簡単で、多くの場合 扱っている速度が光速$c$( $2.997925\times10^8$ m/s)に比べてはるかに小さいからである。

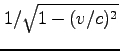自然現象を記述する際に、どうしても特殊相対論が必要になってくる場合が二つある。一つは光速に近い運動が巨視的に起こりうる宇宙現象を扱う場合で、もう一つはミクロの世界でほぼ光速で運動している素粒子を扱う素粒子物理学の世界である。たとえば、CERNのLHC (Large Hadron Collider)において、陽子は光速の0.999999991倍の速度まで加速されるそうだ。以下で示すように速度$v$で運動している物体のエネルギーは $1/\sqrt{1-(v/c)^2}$倍になるから、LHCの場合、これは約7400倍である。陽子の静止エネルギーは0.938 GeVなので、LHCで加速された陽子（と反陽子）は約7 TeVのエネルギーを持つことになる。LHCでは陽子と反陽子を合わせて14 TeVのエネルギーで正面衝突させてそれらを破壊し、陽子、反陽子が宇宙に誕生する以前、ビッグバン直後の状態を再現することによって、素粒子の起源、宇宙の起源に迫る。