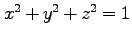 |
(5) |
![]() になることを、当たり前だけど念のために確認しておこう。ここで定義した
になることを、当たり前だけど念のために確認しておこう。ここで定義した![]() 軸の
基底ベクトルを、それぞれ
軸の
基底ベクトルを、それぞれ
![]() とすると、
とすると、
黄道座標系に基づいた、![]() 軸,
軸,![]() 軸,
軸,![]() 軸と、それぞれの基底ベクトル、
軸と、それぞれの基底ベクトル、
![]() を考えよう。
を考えよう。![]() 軸は春分点を向いていて、
軸は春分点を向いていて、![]() 軸
面が黄道面に一致している。同様に、銀河座標系に基づいた、
軸
面が黄道面に一致している。同様に、銀河座標系に基づいた、
![]() 軸,
軸,![]() 軸,
軸,![]() 軸と、基底ベクトル
軸と、基底ベクトル
![]() を考える。
を考える。![]() 軸は銀河中心を向いていて、
軸は銀河中心を向いていて、![]() 平面は銀河面と一致している。
平面は銀河面と一致している。
式(6)で定義した方向ベクトル![]() を、黄道座標系でも銀河座標系でも
表わすことができる。
を、黄道座標系でも銀河座標系でも
表わすことができる。
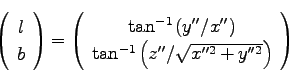 |
(8) |
以上まとめると、ある天体の赤経、赤緯
![]() を銀経、銀緯
を銀経、銀緯![]() に
変換するには、式(5)によって赤道座標系での方向ベクトルの3成分
に
変換するには、式(5)によって赤道座標系での方向ベクトルの3成分![]() を求め、それを
式(7)によって銀河座標系の3成分
を求め、それを
式(7)によって銀河座標系の3成分![]() に変換し、
さらに式(9)を用いればよい。
に変換し、
さらに式(9)を用いればよい。