


Next: 楕円軌道
Up: 二体問題
Previous: 換算質量
地球の周りの人工衛星の軌道や、太陽のまわりの惑星の軌道を考えてみよう。以下で、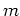 は人工衛星または惑星の換算質量、
は人工衛星または惑星の換算質量、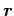 は、
地球中心に相対的な人工衛星の位置、あるいは太陽に相対的な惑星の位置を示す。
まず、エネルギー保存則から、全エネルギーを
は、
地球中心に相対的な人工衛星の位置、あるいは太陽に相対的な惑星の位置を示す。
まず、エネルギー保存則から、全エネルギーを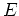 とすると、
とすると、
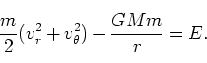 |
(158) |
(153),(154)を使うと、
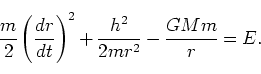 |
(159) |
ここで(154)から、
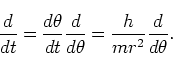 |
(160) |
よって、独立変数を時刻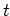 から
から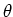 に変換して(159)は、
に変換して(159)は、
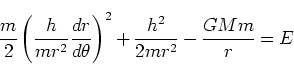 |
(161) |
と書ける。
この微分方程式が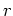 と
と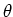 の関係を与えるので、
の関係を与えるので、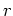 を
を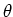 の関数として求めれば、惑星の軌道が求められたことになる。
ここで、
の関数として求めれば、惑星の軌道が求められたことになる。
ここで、 と変数を変換すると、以下のように変形できる。
と変数を変換すると、以下のように変形できる。
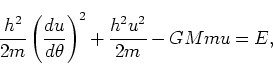 |
(162) |
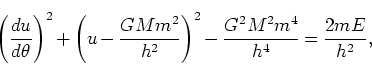 |
(163) |
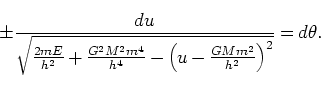 |
(164) |
ここで積分公式、
 を用いて、
を用いて、
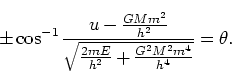 |
(165) |
よって、
 |
(166) |
ここで、
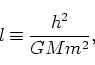 |
(167) |
 |
(168) |
と定義すれば、
(166)は、
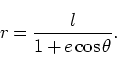 |
(169) |
と書ける。これは原点(太陽または地球)を焦点の一つとする円錐曲線の式で、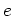 は離心率、
は離心率、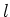 は半直弦と呼ばれる。
円錐曲線は、円錐を任意の断面で切ったときの断面の形で、楕円(
は半直弦と呼ばれる。
円錐曲線は、円錐を任意の断面で切ったときの断面の形で、楕円(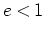 )、放物線(
)、放物線(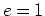 )、双曲線 (
)、双曲線 (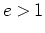 )、のいずれかである。
下図に、異なる離心率の円錐曲線の例を示す。
)、のいずれかである。
下図に、異なる離心率の円錐曲線の例を示す。
実際に太陽の周りの惑星(彗星)や地球の周りの人工衛星(探査機)の軌道も、楕円、放物線、双曲線のどれかである。
(168)より、離心率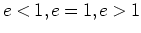 はそれぞれエネルギー
はそれぞれエネルギー 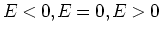 に対応している。すなわち、
全エネルギー
に対応している。すなわち、
全エネルギー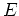 が負のときは、人工衛星は地球の重力に束縛されて、地球の周りを楕円軌道を描いて周回する。
運動エネルギーが増加するにつれ、離心率が大きなり、やがて軌道は放物線となり、人工衛星は地球の重力圏を
脱出する。無限遠でエネルギーはゼロになる。さらに運動エネルギーが大きい場合は、双極線軌道になり、無限遠でも
正のエネルギーを持つ。
が負のときは、人工衛星は地球の重力に束縛されて、地球の周りを楕円軌道を描いて周回する。
運動エネルギーが増加するにつれ、離心率が大きなり、やがて軌道は放物線となり、人工衛星は地球の重力圏を
脱出する。無限遠でエネルギーはゼロになる。さらに運動エネルギーが大きい場合は、双極線軌道になり、無限遠でも
正のエネルギーを持つ。



Next: 楕円軌道
Up: 二体問題
Previous: 換算質量
Ken EBISAWA
2008-01-30
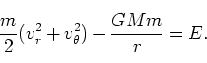
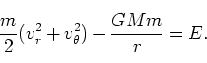
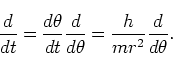
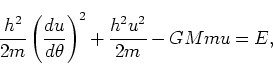
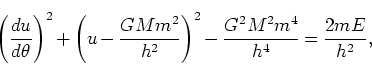
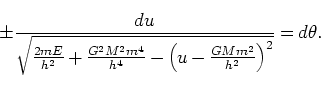
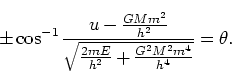
![]() はそれぞれエネルギー
はそれぞれエネルギー ![]() に対応している。すなわち、
全エネルギー
に対応している。すなわち、
全エネルギー![]() が負のときは、人工衛星は地球の重力に束縛されて、地球の周りを楕円軌道を描いて周回する。
運動エネルギーが増加するにつれ、離心率が大きなり、やがて軌道は放物線となり、人工衛星は地球の重力圏を
脱出する。無限遠でエネルギーはゼロになる。さらに運動エネルギーが大きい場合は、双極線軌道になり、無限遠でも
正のエネルギーを持つ。
が負のときは、人工衛星は地球の重力に束縛されて、地球の周りを楕円軌道を描いて周回する。
運動エネルギーが増加するにつれ、離心率が大きなり、やがて軌道は放物線となり、人工衛星は地球の重力圏を
脱出する。無限遠でエネルギーはゼロになる。さらに運動エネルギーが大きい場合は、双極線軌道になり、無限遠でも
正のエネルギーを持つ。