TOP > Report & Column > The Forefront of Space Science > 2010 > Trajectory Design for Interplanetary Missions and Formation Flight of Spacecraft

| 1 | 2 | 3 | Formation flight and periodic orbit Lately, there are higher expectations for formation flights to provide earth-orbiting spacecraft with in-orbit services such as check-up, maintenance/repair and recovery, and to perform highly accurate scientific observations using space telescopes. “Formation flight�Emeans a group of several spacecraft flying in orbit and maintaining specified conditions. In formation flight, the relative position of the satellites is more important than their absolute position. Let me consider the relative motion of the follower and leader satellites in the earth orbit as shown in the left of Fig. 3. The equation to handle relative motion in the area close to circular orbit is called Hill’s Equation. In this equation, simplification called “linearization�Eis performed to obtain an equation that is effective near a reference point (the circular orbit, in this case). Hill’s Equation is frequently used to determine formation-flight orbit because it has a “periodic solution,�Ewhich means that, as long as the satellites have position and velocity meeting the condition at a certain time, they will orbit forever in their trajectories. Thus, if we use the periodic solution, it is possible to put a follower satellite into orbit circling around a leader satellite eternally without use of fuel. This is, however, an ideal case. In practice, the satellite gradually deviates from periodic orbit over a long time as errors generated at linearization accumulate. In that case, another idea pops up. Why not obtain a periodic solution from the “nonlinear�Eequation prior to linearization. In general, it is difficult to obtain a periodic solution from a nonlinear equation. Nonetheless, it becomes possible in the case of formation flight. 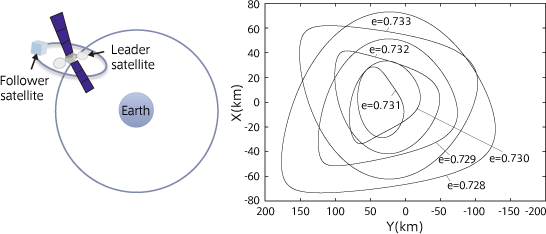Figure 3. Left: Formation flight; Right: Examples of nonlinear periodic orbit Periodic orbit considering nonlinearity We are able to obtain a periodic solution from a nonlinear equation because a periodic orbit of relative motion is also periodic orbit even in an inertial system. In an inertial system, a spacecraft moves according to the well-known Kepler motion, that is, the trajectory should take the form of a circle, ellipse or parabola. Among these, orbits that resulted in circular or elliptical forms are periodic orbits. In an inertial system, a periodic orbit of relative motion should take a circular or elliptical orbit. Using this fact, we can find a periodic solution of a nonlinear equation. Several examples of periodic orbits are shown in the right of Fig. 3. The figure shows the relative motion of a follower to a leader satellite. Elliptical orbits are indicated as distorted ones in an inertial system. Since we can obtain all periodic solutions from a nonlinear equation, it is possible to apply this method to formation flights using periodic orbits of various shapes and sizes. When applied to actual cases, control is required to maintain orbits because some errors are still present in the equation. However, if orbit control consumes too much fuel, the effectiveness of using the periodic obit would be lost. Therefore, we are conducting research on improved control methods as well. Conclusion To reduce a spacecraft’s fuel consumption as much as possible when implementing more complex missions, it is essential to adopt good orbital design methodology that fully incorporates the dynamics of spacecraft. I hope this article successfully conveyed this significance to readers. Mai Bando | 1 | 2 | 3 |

• Back to top