TOP > Report & Column > The Forefront of Space Science > 2010 > Trajectory Design for Interplanetary Missions and Formation Flight of Spacecraft
![]()

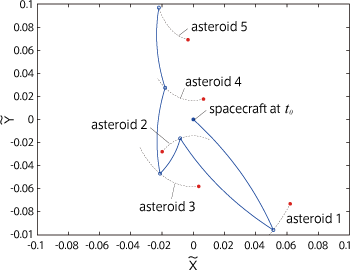
Trajectory design for multiple flybys The use of the generating-function method allows a considerable reduction in computation time for the optimization of multiple flyby trajectories, in which a spacecraft flies by many asteroids in succession. In the past, such trajectory design was impossible due computation limitations. Take for example the spacecraft visiting five out of 100 asteroids near earth as shown in the Fig. 2A. We must select five objects and decide the order for the spacecraft to fly by within a certain time interval so that the required amount of velocity change could be minimized. In this case, in order to select the best trajectory we have to solve the Lambert Problem for a total of 9,034,502,400 cases of permutation and combination. Using the generating function, we can obtain a formula to compute the required total amount of velocity change once we fix the time interval. By substituting the boundary conditions into the formula and calculating the required total amount of velocity change, we can obtain the optimum trajectory (i.e., one with the minimum total amount of velocity change and fuel consumption) as shown in the Fig. 2B. This can be done within practical computation time. In the traditional-design method, since we first decide the target objects and visiting order and then determine a route to minimize fuel consumption, the time interval becomes a design parameter. With the generating-function method, optimization becomes possible by setting the time interval. Thus, we need to be careful in designing the time interval. In addition to the above case, the generating function is useful for and applicable to more difficult cases, such as the trajectory optimization of low-thrust, continuous-acceleration spacecraft. 
|
||||||||||




