天体にはその質量から決まる、エディントン限界 (Eddington limit)と言う
限界光度がある。それ以上明るくなると、輻射圧によって星の大気が飛ばされてしまう。
宇宙にある元素の大部分が水素である。水素の質量を![]() として、重力と輻射圧のつりあいの式は以下のように書ける。
として、重力と輻射圧のつりあいの式は以下のように書ける。
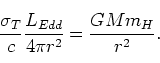 |
(184) |
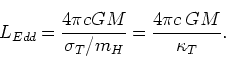 |
(185) |
白色矮星の最大質量(チャンドラセカール限界)は![]() で、それが中性子星の平均質量に対応している。
中性子星の最大質量は
で、それが中性子星の平均質量に対応している。
中性子星の最大質量は![]() で、それより重いコンパクト星はブラックホールである
で、それより重いコンパクト星はブラックホールである![]() 。
ブラックホールについては、(186)に従って、質量が大きいほど、明るく光ることができる。
。
ブラックホールについては、(186)に従って、質量が大きいほど、明るく光ることができる。
前節で示したとおり、![]() erg/sで質量降着している中性子星はほぼエディントン限界で光っていることに
注意。これより質量降着率が大きくなっても、より明るく光ることはできない(物質は降着できずに、輻射圧で
跳ねとばされてしまう)。
erg/sで質量降着している中性子星はほぼエディントン限界で光っていることに
注意。これより質量降着率が大きくなっても、より明るく光ることはできない(物質は降着できずに、輻射圧で
跳ねとばされてしまう)。