�֤��ױ����Υǡ������Ѥ������������μ��̤�Ⱦ�¤���褦
1. �Ϥ����
1.1 �ؽ�����
�֤��ױ�������ܤ��줿������������ɡʣ̣��áˤΥǡ������Ѥ��ơ���̯��ŷ�Ρ������������פμ��̤�Ⱦ�¤���Ƥߤޤ��礦�����β����ǡ���ͭ���Ϥȸ��α�ư�̡��������ͤˤĤ��Ƴؽ����Ƥߤޤ��礦��1.2 ͽ���μ�
Windows �Υѥ�����λȤ����������EXCEL �λȤ����Ϥ��������ΤäƤ����ΤȤ��ޤ���1.3 ���Ѥ���Ķ�
�ġ���- �ţأãţ�
- �֤��ױ�����������������ɤǼ����������Υǡ�����������ä�����Ρ� data folder��Ρ��ʲ� EXCEL �ե������Ȥ��ޤ����� X1608-522_steady.xls, X1608-522_burst.xls , BlackBody.xls
- �ޤ����Ǹ�α�������Ȥ��ơ����ģ��ԣ��ե��������ˡ�X1636-536_No1,X1636-536_No2,X1636-536_No3,X1636-536_No4,��������ޤ����� ��X1636-536_No1.xls, X1636-536_No2.xls, X1636-536_No3.xls, X1636-536_No4.xls
1.4 ��Ϣŷ��
| X�������������������� | X1608-522 |
| �����Ϣ���ϡ��������� | X1608-522 |
1.5 �������
| ������ | ������ |
|---|---|
| ���ļӻҡ����ܤҤȤߡ����ܽ��� | 2008-02-25��2010-01-23 |
1.6 ���ͻ���
�ܲ�������������뤿��λ������Ѱդ��ޤ�����- �֤��ױ����ˤĤ��� (3.1.pdf)
- ���Υǡ��� (3.2.pdf)
- �֤��פ��Ĥ������� (3.3.pdf)
- X���С����ȤˤĤ��� (X-ray_Burst.pdf)
- �������ͤξܤ������� (Blackbody_model.pdf)
- �������ͥ�ǥ�η� (BlackBody_unit.pdf)
2. ���������ˤĤ���
����������̩��ŷ��
���ξϤϾ���������ſ�����������ǯ���إ֥�å��ۡ���ȹ⥨�ͥ륮�����ݡ٤ͤˤޤȤ��ΤǤ���
�����������������οʲ�
�������ʲ����פˤɤΤ褦�ʹ�̩��ŷ�Τ�Ĥ����ϡ������μ��̤ˤ�äƷ�ޤ�ޤ��� ��ñ�����οʲ����ͻҤοޤ˼����ޤ���
���ۼ��̤���0.46�ܤޤǤι������ֿ������Ȥ�ƤФ졢 ���٤��㤤����إꥦ��ˤ����Ф��������Ǥ�Ȥ��Ԥ�������Ϥ��Τޤޥإꥦ����������ˤʤ�ޤ������ۼ��̤��� 0.46�ܤ�����8�ܤޤǤι����Ǥϡ��濴�ǿ��Ǥ�Ȥ��̤�������ǥإꥦ������Ф�ú�ǡ����ǡ����Ǥ�����뤬������ʾ��ȿ���Ͽʤޤ����ֿ��������ʳ���Ф��������Ȥʤ�ޤ��� ���ۼ��̤�8��10�ܤμ��̤���Ĺ����Ǥ�ú�ǡ����Ǥ���ʤ��濴�ˤǤ���˳�ͻ��ȿ���������ꡢ���Ǥ�ͥ��ޥ��ͥ����फ��ʤ�ˤ�����ޤ��������ʳ��dzˤϽ��ह �뤿�ᡢ�ŻҤν��వ�ǽ��Ϥ�٤���褦�ˤʤꡢ���γˤμ��Ϥε�̾�����ʬ��ú��dz�Ƥ��ʤ�Ȥ�����¤�ˤʤ�ޤ����ˤ��괬����ʬ�ǵ������ȿ���� �ֳ��פˤ�äƼ���˳ˤμ��̤������Ƥ����ޤ������䤬���濴�ˤ������븶����ǡ��ۻҤ��ŻҤ���ͤ��������Ҥ��Ѥ�ä��������ͥ륮��Ū�˰���ˤʤ� �褦�ˤʤ�ޤ�������ˤ�ä��濴�ˤ������Ҥ����ʸ��ҳˤ����Ԥ������褦�ˤʤ�ޤ����������Ż���ͤˤ�ä��ŻҤν��వ����ޤ뤿�ᡢ���Ϥ�� �����ʤ��ʤä������Τ���ʼ��̤�Ϥ�ޤ����濴�ˤμ��̤ϡ�̩�٤���ʬ�礭���ʤä������Ҥν��వ�ǽ��Ϥ�٤���褦�ˤʤ����ߤ��ޤ�������� �����ؤϳˤˤ�äƷ㤷��ķ���֤���ƾ��Ȥ�ȯ�������쵤�˿���Ф���ޤ��������ʳ���Ķ������ȯ�ȸƤӤޤ�����ȯ�θ�ˤ������Ҥ���ʤ��̩�٤� �ˤ��Ĥꡢ���줬���������Ȥʤ�ޤ���
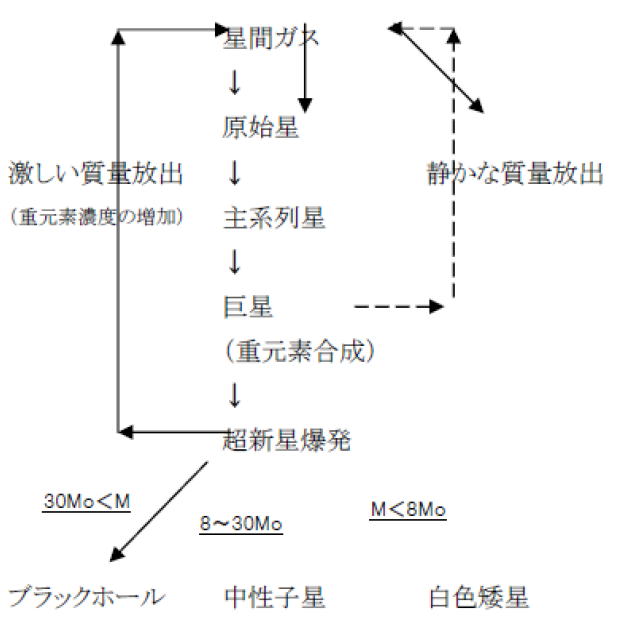
�����ۼ��̤�10 �ܰʾ����������Ǥϡ������˽Ť����Ǥ����Ф��ƤϤ���˽Ť����Ǥ����졢�ǽ�Ū��Ŵ���濴�ˤ�������ʳ��ޤdz�ȿ�����ʤߤޤ���Ŵ���Ҥϸ��ҳˤη� �票�ͥ륮�����Ǥ��礭������ˤ���ʾ�γ�ͻ��ϵ����餺���濴��Ǯ�����ʤ��ʤ뤿���Ŵ���濴�ˤϽ��ϼ��̤��ʤ��鲹�٤�夲�Ƥ����ޤ������٤��� 100 ���٤�ã�����Ŵ�����Ҥ�ۼ����ƥإꥦ���ʬ��Ŵ�θ�ʬ��Ȥ�����Ǯȿ���������Ƶ�˰��Ϥ��ޤ�������ˤ�äƽ��Ϥ�٤����ʤ��ʤꡢ���� �Τ������������٤��Ķ������ȯ�����ޤ�����ȯ�θ�ˤ����̤��줿�Ĥ��Ĥ�ޤ����Ĥä��Ĥμ��̤����ۤ�2-3 �����٤ʤ����������Ȥ��ƻĤ�ޤ���������ʾ�ʤ�н����������ߤޤ뤳�Ȥʤ��֥�å��ۡ���ˤʤ�ޤ���Ķ������ȯ�����ʳ��Ǥɤ����ä����ʤ�Фɤ� ���餤�οĤμ��̤��Ĥꡢ���η�����������ˤʤ뤫�����뤤�ϥ֥�å��ۡ���ˤʤ뤫�Ȥ��ä���̩�ʾ��ϸ��ߤǤϤ��ޤ�Ϥä��ꤷ�Ƥ��ޤ������ۼ� �̤�30 �ܰʾ�ι����Ϥۤܥ֥�å��ۡ���ˤʤ�ȹͤ����Ƥ��ޤ���
������������������
�����������ۼ��̤Σ��ܰʲ����������ͥ륮�����Ǥ�����Ǥ���ơ����ν��Ϥ�٤��륬���������̤�����ΤǤ������ν��Ϥ�٤����Ϥ��Ż� �ν��వ�ǡ������礭���ϣ���������Ǥ���Ϣ���Ϥ���������������ȼ��������̹��夬������ϡ��������μ��Ϥ˹�����פ���������Ƥ��ޤ��� ���ι�����פ�������ɽ�̤DzĻ����糰���Ǹ���ޤ�������ʪ�����̤��Ѳ�������Ѹ����Ȥ��ƴ�¬����뤳�Ȥˤʤ�ޤ���
������������ˤϡ�102��105T (�ƥ���) �ζ����������Ĥ�Τ����ꡢ����ή�ϼ��ˤ�����ޤ������ΤȤ����ˤǾ��Ȥ�ȯ�����ơ�X �������Ф���ⲹ�Υ�������������ޤ��������ζ��٤�����������֥�å��ۡ������٤ƾ�������ΤǤ���
��������������������
���������Ȥϡ����̤��礭�ʹ����ΰ����κǸ�Ǥ���Ķ������ȯ�ˤ�ä����ޤ�롢��Ȥ��������Ҥ�����̩�˽��ޤäƤǤ��Ƥ������Τ��ȤǤ������������ϼ��̤��������١�Ⱦ�¤�10km ���١��絤�θ����ϣ�m ���٤ǡ�̩�٤����ۤ�̩�٤�1014 �ܰʾ�⤢��ޤ�����������������̤ι�����Ķ������ȯ�ˤ�äƤ����濴�ˤ���������ޤ��������������Ȥ���¸�ߤǤ�����̤ˤϾ�¤����ꡢ�����Ķ����ȥ֥�å��ۡ���ˤʤ�ޤ�����¤μ��̤����ۼ��̤�1.5 �ܤ���2.5 �ܤ��ϰϤˤ���ޤ������ϤȤĤꤢ�äƤ���Τϡ������ξ��Υ������ǤϤʤ��������Ҥν��వ�Ȥ����̻��ϳ�Ū�Ĥꤢ���Ǥ���
��X �������ͤ������������ΤۤȤ�ɤϡ������Ҥȹ�����Ϣ���ϤǤ������������Ф��륬���ΰ����Ϲ����ν��Ϸ���ۤ��ơ����������ν��Ϸ���ή����ߤޤ������� ������Ϣ���Ϥβ�ž�ˤ�ꡢ�������˲�ž���ʤ�����������������ޤ������������������˶�Ť���®�٤�®���ʤꡢ���٤�夬�äơ�����Ʊ�Τ����ͤ��ƹ� �������Ȥʤ�ޤ������Υ�������X �������ͤ���ޤ���
�������������֥�å��ۡ���
���֥�å��ۡ��������ϡ�������ȯ����������������ã���뤳�Ȥ�����ʤ��ü�ʶ��֤Τ��Ȥǡ������奿����ν����������β�Ȥ���¸�ߤ��ޤ����� ��å��ۡ�����¬����ľ��Ū����ˡ�Ϥ���ޤ�������Ϣ���������饱�ץ顼��ˡ§���Ѥ��ƿ��ꤵ���X �����μ��̤����ۼ��̤Σ��ܤ���礭��ŷ�Τ�֥�å��ۡ���������ȸƤ�Ǥ��ޤ���
���֥�å��ۡ����Ϣ���Ϥξ��ˤϡ�ȼ������ι���Ǽ��Ϥ˹ⲹ�ι�����פ����������줬���������ͤ��ޤ���X���Υ��ͥ륮�����ڥ��ȥ������������Ʊ���褦�˹������ͷ��Τ�Τ䡢�٤��ؿ����Τ�Τ�����ޤ���
����������������
���ξϤϡ��ƺ���������������ǯ�������������ȥѥ륵���٤ͤˤޤȤ��ΤǤ���
����������������������
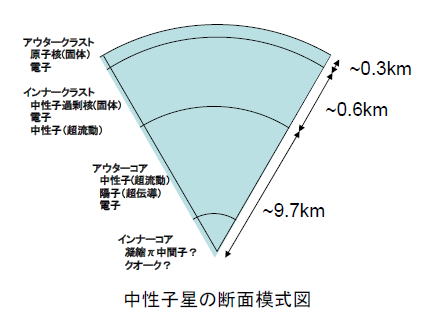
�ʲ��οޤ˼������������Τ����Ĥ�����ħŪ���ؤ�¦�����������ޤ������ؤϤ����褽̩�٤ˤ�ä�ʬ�����Ƥ��ޤ���
ɽ����
ɽ���ؤ�̩�٤�109kgm-3�ʲ����ΰ�ǡ����٤伧��ˤ�äƸ��Τޤ��ϱ��ξ��֤ȤʤäƤ��ޤ���
�����������饹��
ɽ���ؤβ��ˤ����ؤǡ����褽��ɴ���θ���������ޤ���̩�٤�109��4.3��1014gm-3 �Ǥ��������ΰ�Ǥ�Ŵ��˥å���ʤɤθ��ҳˤ��ʻҾ����¤ӡ����ΤȤʤäƤ��ޤ�����§Ū���¤�����ҳˤϡ����ष���ŻҤγ�����˿��äƤ��ޤ���̩�٤�1010gm-3 ��Ķ����ȡ��ŻҤΥե���ߥ��ͥ륮����1MeV �ʾ�Ȥʤ�ޤ�������ȸ��ҳ�����ۻҤ��ŻҤ���ͤ��������Ҥ��Ѥ��ޤ��� ��̩�٤��⤯�ʤ�ˤĤ���Ż���ͤ����ʤߡ������Ҳ��θ��ҳˤ��Ǥ��ޤ��������̩�٤��⤯�ʤ�ˤĤ�ơ�ɽ�̥��ͥ륮�������ʤ��Ƥ���ʻҤ�¿���� �ҳˤ�����ˤʤ�ޤ������Τ褦�ʸ��ҳˤ��ϵ��Ǥ�����û���֤��������Ƥ��ޤ��ޤ������������������Ǥ����˰��Ϥ��⤤����˰��ꤷ��¸�ߤǤ��� ����
����ʡ����饹��
���褽������θ����ǡ���0��2.8��105������3 ��ɸ�ึ�ҳ�̩�٤Ȥ���ȡ�̩�٤�0.5��0 ��꾮�����Ǥ�����ͳ�����Ҥ������Ҳ��ʸ��ҳˤ������ष���ŻҤγ�����˳ʻҾ����¤��¸�ߤ��Ƥ��ޤ����ޤ��������ΰ�Ǥ������Ҥҳˤ����«�� ���Ƥ������Ȥ��Ǥ����������Ҥΰ��������ҳˤ�����ФƤ��ޤ������Ф������Ҥ�Ķήư���֡��Ĥޤ�Ǵ�굤���ʤ��ʤꡢ���餵���ή���Ķή�Τ�ʤä� ���ޤ��������ΰ�ˤϸ��ҳˤȼ�ͳ�ŻҤȼ�ͳ�����Ҥ�¸�ߤ��ޤ���
������������
̩�٤Ϥ��褽0.5��2��0 �Ǥ��ꡢ��km �θ����Ǥ������ҳˤϤ��٤��Ϥ��Ƥ��ޤ���������Ķήư���֤ˤ��뼫ͳ�������Ҥ������Ƥ��ޤ������ѡ�����Ȥ��Żҡ��ߥ塼����ʤɤβ���γ�Ҥȡ�Ķ��Ƴ���֤��ۻҤ�ޤޤ�Ƥ��ޤ��������϶������ष�Ƥ��ޤ���
����ʡ�����
��km ���٤θ����ǡ����������Τ��Ф��ƤϤ��������ʲ���ˤ��ۤʤ�ޤ���̩�٤�2��0 ����礭�����濴����̩�٤϶ˤ�ƹ⤯��10��15��0 �ˤ�ã���ޤ���
2.2.2.���������ˤ��������ȯ���λ��Ȥ�
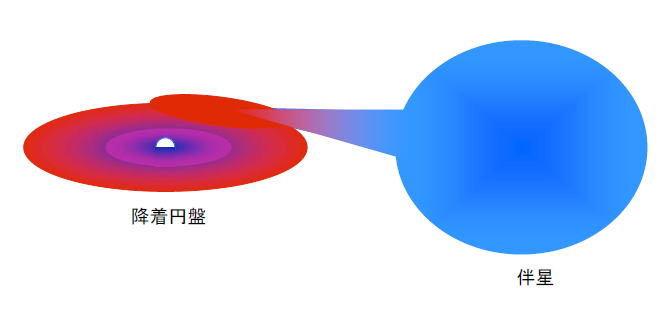
�桹�ζ�ϷϤˤϣ�����¿�̤����ͤ���ŷ�Ρʣ������ˤ���ɴ�Ĥۤ�¸�ߤ��ޤ���X �������ͤ������������ΤۤȤ�ɤϡ������Ҥȹ�����Ϣ���ϤǤǤ����������������������˼��̤����夹��Ƚ��ϥ��ͥ륮���������ƣ��������ͤ��ޤ����������äƣ���Ϣ���ϤȤ⤤���ޤ���X ��ȯ���λ��Ȥߤ�����������Ϣ���Ϥξ�������������ޤ���
������������������ȼ���ˤ��ʲ�����ĥ����ȡ��������γ��ؤϤ��ν��Ϸ������졢���ΰ����ϡ����������ν��Ϸ���ή����ߤޤ���ή������ʪ���ϳѱ� ư�̤���äƤ���Τǡ����������μ���˹�����פȸƤФ�륬���α��פ���ޤ������ι�����פ���Ǥϡ�������ʪ���ۤ�®����®�٤DZ�ư���Ƥ���Τǡ� ��¦�ȳ�¦��ʪ���δ֤���Ϥ�Ư���ޤ���������dzѱ�ư�̤��ʤ��顢ʪ���Ϥ餻��������������˸����ä�����Ƥ����ޤ���
���������μ��줬�����Ȥ��ϡ��ץ饺�ޤǤ��������פΥ����ϼ���ˤ�äƤ����ߤ��졢���θ弧�����˱�ä�ή�졢�����ն�˽�����ޤ������� �ն����������ʪ���ϡ�����������ɽ�̶������ʥ��ͥ륮�����������X �������Ф��ޤ���2 �Ĥμ��ˤ���������ž���Ȱ��פ��Ƥ��ʤ���硢������������®�Ǽ�ž���Ƥ���С�X �������Ф����������Ѥ��ʤ����������Τǡ����ͤ����������μ�ž��ȼ�äơ���¬�Ԥ����ξ�ˤΥץ饺�ޤ��줬��ߤ˸����뤳�Ȥˤʤꡢ�����ѥ륵���Ȥ� �ƴ�¬����뤳�Ȥˤʤ�ޤ������������μ��줬�夤�Ȥ��ϡ�������פ�����������ɽ�̶�ޤǿ������ޤ���ʪ��������������ɽ�̤ι����ϰϤ�������ߤ� ��������������ɽ�̤����Ѥ�������ʪ���ϡ�̩�٤Ȳ��٤���ͻ��ξ������������֤ˤʤ����ȯŪ�ʳ�ͻ��������ⲹ��������������X �������ͤ��뤳�Ȥ�����ޤ����ޤ�����ǹⲹ�ˤʤä�������פ����X �������Ф���ޤ���������פ����������ζ���Ĥ졢Ǯ���ץ饺�ޱ����Ǥ��ޤ���
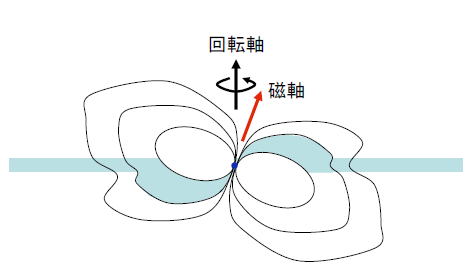
�������������������������줬��������ʪ����ή��
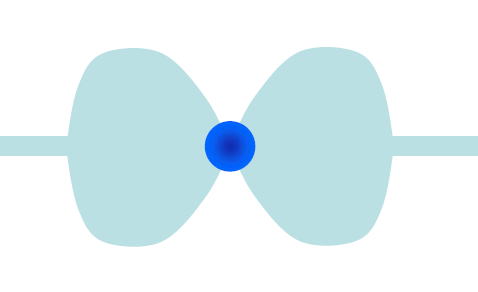
���������������������������줬�夤����ʪ����ή��
3. �֤��ױ���
�֤��ױ����ϡ�1987ǯ���Ǥ��夲��줿�������ˤ��ŷ�δ�¬�Τ���˿� �����Ǥ���1991ǯ�ޤdz������ޤ�����4000 cm��������Ѥ��������������� �ɤ���ϴ�¬���֤Ȥ��ơ�����������֥�å��ۡ���δ�¬�Ǥ�¿���ζ��Ӥ�� ���Ƥ��ޤ������ζ���Ǥϡ����Ρ֤��ױ����Υǡ������Ѥ��ޤ����ܤ�����
���ɤ�Ǥ���������
4.���������μ��̤���Ƥߤ褦
�����������ǥ���ȥ�³����٤ȼ��̤ε����
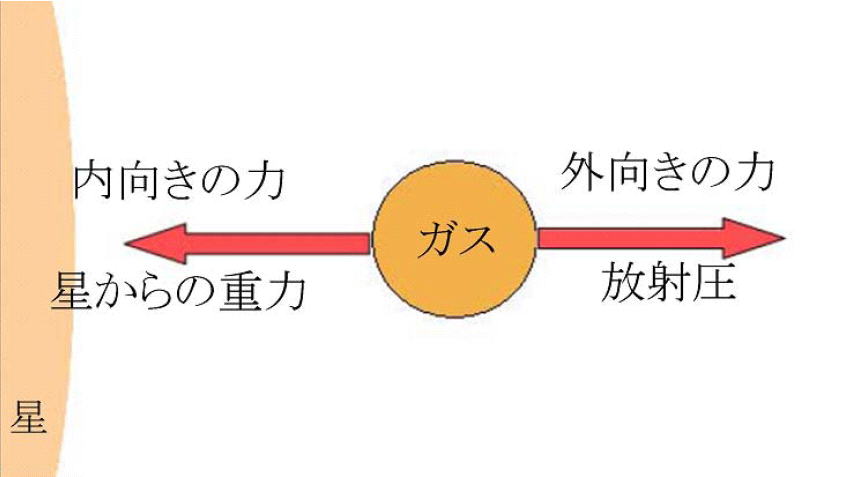
�����ϥ����Τ����ޤ�Ǥ������������������륬�������뤤�ϡ����γ��ˤ��륬���Ͻ���(��ͭ���ϡˡ���������ϡˤ�«������Ƥ��ޤ�������������
�ϸ���Ф��Τǡ������ˤ��Ƥ����Ф����Ȥ����ϡ����Ͱ������������ϡˤ�Ư���ޤ������ν��Ϥȸ��ˤ�����Ф����Ȥ����Ϥ����礦�����������뤵��
�ǥ���ȥ�θ³����٤Ȥ����ޤ������Ͱ��Ȥϡ������������鱿ư�̤���ä��Ƥ����Ф�����ϤΤ��ȤǤ��������ϼ�˿��ǥ����Ǥ������ǥ������ŻҤ�Ҥ�
�Ļ��äƤ��ơ������ŻҤ������Ƥ����Ф���ޤ��������鸫����ŻҤ����Ѥ����Ū�ˤ����͡�![]() �����٤˸����ޤ�������
�����٤˸����ޤ�������![]() ��ȥॽ���������ѤȸƤӤޤ����������ͥ륮����
��ȥॽ���������ѤȸƤӤޤ����������ͥ륮����![]() �θ���
�θ���![]() �α�ư�̤�����ޤ��������ǡ���ϸ���®�٤Ǥ���
�α�ư�̤�����ޤ��������ǡ���ϸ���®�٤Ǥ���
�����꣱��![]() ����ñ�̤Ϥɤ��ʤ�Ǥ��礦����
����ñ�̤Ϥɤ��ʤ�Ǥ��礦����
�� ��������θ��١����ä���������ͥ��ͥ륮���ˤ�![]() �Ȥ���ȡ������濴����
�Ȥ���ȡ������濴����![]() �ΰ��֤ˤ�ñ�����Ѥ�����
�ΰ��֤ˤ�ñ�����Ѥ�����![]() �Υ��ͥ륮������äƤ��ޤ������ä�
�Υ��ͥ륮������äƤ��ޤ������ä�![]() �Υ��ͥ륮���θ������Ǹ��Ҥ��ŻҤ�Ϥ������Ф��ޤ������λ�ʿ��Ū�˸������äƤ��뱿ư�̤���Ǹ��Ҥ��Ϥ��Ƥ��ޤ��Ȥ���ȡ����ä�����
�Υ��ͥ륮���θ������Ǹ��Ҥ��ŻҤ�Ϥ������Ф��ޤ������λ�ʿ��Ū�˸������äƤ��뱿ư�̤���Ǹ��Ҥ��Ϥ��Ƥ��ޤ��Ȥ���ȡ����ä�����![]() �α�ư�̤���Ǹ��Ҥ��㤦���Ȥˤʤ�ޤ�������������ʿ��Ū�����;��˽ФƤ���Τǡ���ư�̤����;��Ǥ������ʤ�����ǥ������������������(���Ͱ��ˤ�
�α�ư�̤���Ǹ��Ҥ��㤦���Ȥˤʤ�ޤ�������������ʿ��Ū�����;��˽ФƤ���Τǡ���ư�̤����;��Ǥ������ʤ�����ǥ������������������(���Ͱ��ˤ�
![]()
�ǡ�����ϡ������鸫�����;����Ƥ����Ф��ϤȤʤ�ޤ���
�����������Ǹ��Ҥμ��̤ϡ��ۤ��ۻҤμ���,![]() ,�Ǥ������μ��̤�
,�Ǥ������μ��̤�![]() �Ȥ���ȡ������濴����Ⱦ��
�Ȥ���ȡ������濴����Ⱦ��![]() �ΰ��֤ˤ�����ǥ�������������ϡ���ͭ���ϡˤ�
�ΰ��֤ˤ�����ǥ�������������ϡ���ͭ���ϡˤ�
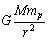
�ǡ����˰����դ�����������Ư���ޤ������Ͱ������Ѷ����ʤ�ȡ����Ϥ����Ͱ����ߤ�礦��礬����ޤ������λ������θ��٤�![]() �Ȥ���ȡ�
�Ȥ���ȡ�
![]()
�Ȥ����ط�������Ω���ޤ�������![]() �ǥ���ȥ�θ³����٤Ȥ����ޤ��������ǡ�
�ǥ���ȥ�θ³����٤Ȥ����ޤ��������ǡ�![]() ,c��
,c��![]() �Ͻ����������®���ȥॽ���������ѡ�
�Ͻ����������®���ȥॽ���������ѡ�![]() ,
,![]() ,
,![]() ,�����μ��̡��ۻҤμ��̡���������ǥ����ޤǤε�Υ�Ǥ������ǥ���ȥ�θ³����٤���������Ū�����ͤǤ������¤��礭���Ǥ�����ľ����
,�����μ��̡��ۻҤμ��̡���������ǥ����ޤǤε�Υ�Ǥ������ǥ���ȥ�θ³����٤���������Ū�����ͤǤ������¤��礭���Ǥ�����ľ����
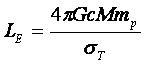
�Ȥʤ�ޤ���
�����δط���դ��Ѥ���ȡ����ǥ���ȥ�θ³����٤�ʬ��������������μ��̤�������Ȥ������Ȥˤʤ�ޤ���
���������֤��ױ����Υǡ����Ƥߤ褦
����������Ϣ���Ϥ� �����С���������ͭ̾��ŷ�Τǣأ��������ݣ������Ȥ���ŷ�Τ�����ޤ��������С����Ȥ���ŷ�Τ�����С��������ȸƤӤޤ����֤��ױ����Ǽ������������Σأ��������ݣ������Ȥ��������С��������Υ��ͥ륮�����ڥ��ȥ��ţأãţ̤Υ�������ȤȤ��ƽ��ǡ�����X1608-522_steady.xcl�ˤ����ޤ���������å����Ƥɤ�������¸���Ʋ����������θ塢��¸�����ե�������Ƥߤޤ��礦�����ʤ���X1608-522_steady.xcl���Ȥ���̾���� "steady" �Ȥ����Τϡ�����ŷ�Τϣ����С����Ȥ����ΤǤ������������Ƥ��ʤ��Ȥ��������ʤ�����ʡ�steady)���֤Υǡ����Ȥ�����̣�Ǥ���
���ޤ��ǡ������ǧ���ޤ������ǡ��������Ȥβ��ˤ��륿�֤���X1608-522 data�פȤʤäƤ��뤳�Ȥ��ǧ���Ʋ������������Ǥʤ���С����Υ��֤�å����ơ���X1608-522 data�פΥ����Ȥ�ɽ�����Ƥ����������ޤ��ǡ����ΰ�̣�����ޤ��礦�����Υǡ����ϡ����ͥ륮�����ڥ��ȥ�Ȥ��äơ�ŷ�Τ����äƤ����������ң� �ģ��ĤΥ��ͥ륮����¬�ꤷ���ɤΥ��ͥ륮���ˤɤ줯�餤��������Σ�������äƤ��������Ƥ��ޤ������ͥ륮�����Ǥϣ������ΰ�ʥ��ͥ륮���Х� �ɤȤ����ޤ��ˤ�ʬ�ष�Ƥ��ޤ���ʬ��λ��������ȣ����ɽ���Ƥ��ޤ���������ϳƥ��ͥ륮���ΰ���濴�Υ��ͥ륮���ǡ�����Ϥ����ΰ������Ⱦʬ��ɽ ���Ƥ��ޤ��������ܤ��飱�����ܤޤǤ������ĤΥ��ͥ륮���Х�ɤΥǡ�����ɽ���Ƥ��ޤ������Ȥ��С������ܤϣ�������keV���濴������Ⱦʬ�� 1.15keV���ΰ�Ǥ��뤳�Ȥ��Ƥ��ޤ������ʤ��0keV ����2.3keV�Ȥ������ȤǤ���
���ꣲ�������ܤΥХ�ɤΥ��ͥ륮���ϰϤϤɤ�����ɤ��ޤǤǤ�����
������ϡ��ƹԤΥ��ͥ륮���Х�ɤˤϤ�����������������ꡢ�����������ꡢ���줫�飱��eV������ˡ�ʿ�Ѵ��Ĥ�äƤ��� �������Ƥ��ޤ�����keV������ˤ��Ƥ���Τϡ�������ͳ�ˤ��ޤ������Ȥ��У������ܤ��飱�����ܤΣ�������ܤ��Ƥ������������ͥ륮���Х�ɤ������� ���飱�����ܤ���٤ƣ��ܡ������ʤäƤ��ޤ���ŷ�Τ����뤵��Ʊ���Ǥ⡢�������ͥ륮���ϰϤΥ��ͥ륮���Х�ɤˤϤ�������Σ�������äƤ��ޤ����դˡ� �������ͥ륮���Х�ɤδ֤ˤϤ��ޤ�����Ϥ�äƤ��ޤ����Τ褦�ˡ����ͥ륮���ϰϤˤ��㤤��ʤ�������ˡ��ǡ�����1keV������Ȥ��Ƥ��ޤ��� �ޤ��������˼������ǡ����ϡ��ºݤ�������ǡ����ȤϾ����ۤʤꡢ���д��������������ɡˤ��������ˤ����̤��������Ƥ���ޤ���
�����˥���դƤߤޤ��礦���ǡ��������Ȥβ��ˤ��륿�֤Ρ�X1608-522 Spectrum�פΥ��֤�å����ơ����Υ����Ȥ�ɽ�����Ƥ������������������ͥ륮���ǽļ����ƥ��ͥ륮���ӥ�����á��������� ���ꡢ��keV�Υ��ͥ륮���ϰϤ����ꤤ���ĤΣ�������äƤ����Τ����Ƥ��ޤ����ƥǡ������β������ϥ��ͥ륮���Х�ɤ��ϰϤ�ɽ���Ƥ��ޤ������Υ� ��դǤϽļ��ⲣ�����п���ɽ���Ƥ��ޤ������줬���֤��ױ�����������������ɤ�¬�ꤷ�Ƶ����أ��������ݣ������Ȥ���ŷ�Τ���Σ����Υ��ͥ� �������ڥ��ȥ�Ǥ���
4.3.���ͥ륮���ե�å�������褦
�����ơ����������μ��̤���뤿��ˤϡ��ޤ����ͥ륮���ե�å�������� ���Ȥ�ɬ�פǤ������ͥ륮���ե�å����Ȥϴ�¬����1 m2�������1�ô֤��̲� ������ҤΥ��ͥ륮���Τ��ȤǤ����ե�å�����ñ�̤ϡ�[keV/sec/m2] �Ǥ���
����1608-522�Σ����Υ��ͥ륮�����ڥ��ȥ�ϡ����������ʥ��ͥ륮���Х�ɤǤ�1keV�����꣱����������������̲᤹����Ҥο���[Photons/keV/sec/m2]�ˤ��Ƥ��ޤ������Υǡ�����Ȥ��Ф����ˡ���¬�ϰ���Υե�å����ϵ����ޤ����ţأãţ̤�ȤäƼºݤ˹ԤäƤߤޤ��礦��
���ޤ����ƥ��ͥ륮���ӥ���Υ��ͥ륮���ե�å�������Ƥߤޤ��礦���ޤ��ϥǡ��������Ȥβ��ˤ��륿�֤Ρ�X1608-522 ������פΥ��֤�å����ơ����Υ����Ȥ�ɽ�����Ƥ�������������Ρ֣�����������1keV���������ä�ʿ�ѣ����ο��פˡ�����Ρ֣����Υ��ͥ륮���Τۤ�ʿ�ѤǤ���ƥӥ���濴���ͥ륮���פ�ݤ�������ˡ�����Σ��ܤΡ֥��ͥ륮���ϰϤ����פ�ݤ���С��ƥ��ͥ륮���ӥ���Ρ�1 m2�������1�ô֤��̲᤹����ҤΥ��ͥ륮���פȤʤ�ޤ���
�������ǡ� ����
������������E��ˡ���=D4*B4*C4*2 ������Ƥߤޤ��礦����������С����Ǥ��ޤ���
����
���������ϡ����Σ�����E����ܤ��顣�����������ܤޤǥ��ԡ����ޤ��礦������ǡ��������ΥХ�ɤdzƥ��ͥ륮���Х����Υ��ͥ륮���ե�å��������Ǥ��ޤ�����
����
�����������ǡ�˺��ʤ��褦��E�ԣ�������Ƥ�ʬ�������������Ȥ��С����ã�����������Υ��ͥ륮���Х����Υ��ͥ륮���פ��줫E�ԣ���ˤ�ñ�̤��Ȥ��С�keV/sec/m2/���ͥ륮���Х�ɡפȽޤ��礦�� ����
���������Ȥ������Υ��ͥ륮���Х�ɤι�פ�Ĥ���Ф褤�Ǥ��͡�E���Ԥˡ�=sum(E4:E15) ������ƤߤƤ�������������ǡ��֤��ױ�����������������ɤǴ�¬�����������ͥ륮���Х�ɤι�פ����ã�����������Υ��ͥ륮���������ޤ��� ����
�������Ǹ�ˡ�E���ԡ��������Ȥ��ơ�C��16�Ԥˡֹ�ס�keV/m2/sec)�פȽƤ����ޤ��礦��
�� �����Ǥϡ�E���Ԥˡ֤��ױ�����������������ɤǴ�¬�����������ͥ륮���Х�ɤι�פ����ã�����������Υ� �ͥ륮������ޤ������ºݤϴ�¬���Ƥ��ʤ��ϰϤ�����Τ������ͥ륮���ǤϤʤ��ΤǤ������أ��������ݣ������Ȥ���ŷ�Τϼ�ˡ����ε����ͥ륮���� �Ϥǥ��ͥ륮�������ͤ��Ƥ���Τǡ����Ū�褤����ȤʤäƤ��ޤ��������Ǥϡ������ͥ륮���ϰϤ���ʬ����ʪ�ȹͤ���ñ�̤��keV/m2�פȤ��ޤ�����
�����ˡ����ͥ륮����ñ�̤�keV�����顡�ʤ��Ѵ����ޤ��礦����1keV �ϡ�������10-16���ʡ��Ǥ����ţ�C�ţ̤���äơ�D���Ԥˤ����ͤ����Ǥ���ޤ��Τǡ�E���Ԥˡ���=E16*D18 ���Ǥ�����С����ͥ륮���ե�å����� J/sec/m2���ޤ��ϡ�W/m2���ǵ��뤳�Ȥ��Ǥ��ޤ�����
��
4.4���������θ��٤ȼ��̤β���
�ޤ��������ͥ륮���ե�å����������������θ��٤���Ƥߤޤ��礦�����٤Ȥϡ�����������1�ô֤���������Ф��륨�ͥ륮���Τ��ȤǤ��������DZ�����X1608-52�ε�Υ��![]() �ȽȤ��ޤ��礦����������ȡ��ե�å���
�ȽȤ��ޤ��礦����������ȡ��ե�å���![]() �ȸ���
�ȸ���![]() �δط���
�δط���![]() �Ǥ���
�Ǥ���
����������������X1608-52�ε�Υ![]() �Ϥ褯ʬ���äƤ��ޤ�����ޤǤδ�¬����X1608-52�϶���濴������ǡ����褽8�������٤Ǥ���ȹͤ����Ƥ��ޤ������Ρ֣���פȤ����Τϡ֥����ѡ������פ��ɤߤޤ���ŷʸ�ؤǤ褯�Ȥ����Υ��ñ�̤Ǥ���������Ϥ��褽3.1��101��[m]�Ǥ���
�Ϥ褯ʬ���äƤ��ޤ�����ޤǤδ�¬����X1608-52�϶���濴������ǡ����褽8�������٤Ǥ���ȹͤ����Ƥ��ޤ������Ρ֣���פȤ����Τϡ֥����ѡ������פ��ɤߤޤ���ŷʸ�ؤǤ褯�Ȥ����Υ��ñ�̤Ǥ���������Ϥ��褽3.1��101��[m]�Ǥ���
����ۤ�4.3�Ϥ�X1608-52�Υ��ͥ륮���ե�å����� E���Ԥ˵��ޤ�����
�������Ԥ˿����Υ�Σ�[����]��D���Ԥ˽Ƥ�����㤫����ؤδ�����3.1��101��[m/kpc]��Ȥäơ�E���Ԥ�[m]��ɽ������Υ����ޤ��礦��E���Ԥˡ���=B19*D19 ���������Ƥ���������
�����˸��٤�E���Ԥˡ���=E18*4*pi()*E19^2 ����������и��٤��Фޤ��������ǡ�pi()�פȤ����Τϡ��֦Сס����ʤ����3.141592..��.�λ��Ǥ���
�����ꣳ,�����٤�ñ�̤Ϥɤ��ʤ�Ǥ��礦����
�� �Ǹ��˺��ʤ��褦�ˡ�F��18�Ԥ��飲���Ԥޤǡ�ñ�̤����Ǥ���������
���ơ����٤���뤳�Ȥ��Ǥ����ʤ顢���ȤϷ�����������������μ��̤β����ͤ���ޤ�ޤ��������������ǥ���ȥ�³����٤ȼ��̤ε��������Ĵ�٤��褦�ˡ����Ϥ����Ͱ������礦��硢
![]()
�Ȥʤ�ޤ����������顢���ǥ���ȥ�θ³����١�![]() ����
����
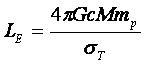
��ɽ�����Ȥ��Ǥ��ޤ������δط����ѷ�����С����������μ���![]() ��
��
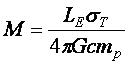
�Ȥʤꡢ�������ǵ��뤳�Ȥ��Ǥ��ޤ�������ɬ�פ������ʲ���ɽ�˼����ޤ���
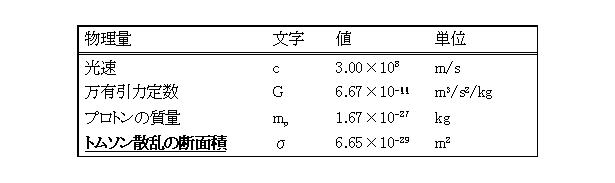
�ʾ����������ƤϤ���
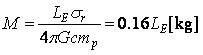
�Ȥʤꡢ��ñ�˷��Ǥ��뤳�Ȥˤʤ�ޤ��������ǡ�![]() ��ñ�̤ϡ��ʡ�s �ޤ��ϡ��ס��Ǥ���
��ñ�̤ϡ��ʡ�s �ޤ��ϡ��ס��Ǥ���
�����������������ǵ����٤ϡ����ǥ���ȥ�θ³����٤����㤤���٤Ǥ���Ϥ��ǡ�![]() �ǤϤ���ޤ������٤�
�ǤϤ���ޤ������٤�![]() ������˻ȤäƵ��������������μ��̤ϼºݤ����������μ��̤�꾮�����ʤ�Ϥ��Ǥ����Ĥޤ����������μ��̤β����ͤ������뤳�Ȥˤʤ�ޤ���
������˻ȤäƵ��������������μ��̤ϼºݤ����������μ��̤�꾮�����ʤ�Ϥ��Ǥ����Ĥޤ����������μ��̤β����ͤ������뤳�Ȥˤʤ�ޤ���
���Ǥϡ��ºݤ�X1608-522�����������μ��̤β����ͤ���Ƥߤޤ��礦��D���Ԥδ�����0.16��Ȥäơ�E���Ԥˡ�=E20*D21 �����������[kg]��ñ�̤Ǽ��̤β����ͤ���뤳�Ȥ��Ǥ��ޤ��� ��
�����ꡡ4�� �����������μ��̤����ۼ��̤���ӤƤߤޤ��礦�����ۼ���Mo�� Mo=1.99��1030 [kg]���Ǥ���
���������Ƶ���X1608-52�μ��̤β����ͤ����ۤ���٤Ƥ����֤����ʤ�Ȼפ��ޤ���X��������-���������뤵����ư����Τǡ���ä����뤤 �Ȥ��Υǡ�����Ȥ��С�����礭�ʲ����ͤ���ޤꡢ���������������μ��̤˶�Ť��ޤ������Ȥ��С������С����Ȥλ��Ϥ�ä����뤤�Τǡ�����礭�ʲ����� ��������Ǥ��礦��
�����β��Ϥǵ����٤ϡ����ǥ���ȥ�θ³����٤����㤤�Τǡ������������줿���������μ��̤⡢�ºݤμ��̤���ɬ���������ͤˤʤ�Ȥ� �����Ȥ˲ä��ơ�������ˡ�����������μ��̤������ˤĤ��ơ����դ��ʤ���Фʤ�ʤ��������Ĥ�����ޤ�������Ǥ���Х��ͥ륮���ϰϤ�����̵���� �ޤ���ʬ���٤��Ǥ��������ͥ륮���ϰϤ�֤��ױ�����������������ɤ���¬�����ϰϡʤ��褽1��30[keV]�ˤ˸¤äƲ��Ϥ������Ȥ�ޤ������� �����μ��̤������뤳�Ȥθ����ˤʤ�ޤ����ޤ������ֵۼ����θ���Ƥ��ʤ��������������μ��̤������뤳�Ȥ��װ��Ȥʤ�ޤ����������������� �Ф��줿�����Τ����Ĥ��ϡ����д�ˤ��ɤ��夯�ޤǤ����֥������ˤ��ۼ����졢���д�ˤ��ɤ��夯���Σ����ο��ϡ����Ф��줿�Ȥ��Σ����ο���꾯�ʤ� �ʤäƤ���Ϥ�������Ǥ���
���Ĥޤꡢ
����* ���ǥ���ȥ��ߥåȡʸ³����١ˤζ�ޤǸ��٤��礭���ʤäƤ���Ȥ��Υǡ������Ѥ��뤳��
����* ���ͥ륮����̵����ޤǹ�θ���뤳��
����* ���ֵۼ����θ���뤳��
�ǡ�����礭�ʼ��̤β����ͤ�������Ȥ������ȤǤ���
��.����������Ⱦ�¤���Ƥߤ褦
������������
�����ϡ�����������Ⱦ�¤Ǥ��������Ǥϡ�X���С������Ȥ������ݤ�Ȥ��ޤ�������������Ⱦ�¤�������ˡ��ޤ��ϡ����ο����äޤ��礦��
�����Ȥ��С��ȶ�ʸ��ݤȤ���ú�Ф�ͤ��Ƥߤޤ��礦��ú�Фε����ϡ����ޤ�Ǯ���ʤ������֤���������������������ޤ������٤��夬��Ǯ���ʤ� �Ȳ����äݤ��ʤ굱���������ޤ����������Ŵţ������Ƥߤ�ȡ����Ф餯�����Ŵţ��Ʊ���褦�ʸ��������ޤ����Ǥϡ��ʤ��������㤦ʪ����Ʊ�����θ����� �ĤΤǤ��礦���������ϡ��嵭�ξ����Ǥϲ��٤����Ƿ�ޤ������������ˤʤ뤫��Ǥ���
�����벹�٤Ȥ��ƹͤ�������Ǥ�����ξ�硢���ο��ϡ����٤ˤ�ä��Ѳ����ޤ��������Ʊ�����θ��Ǥ���С�ñ����������������ͤ������ζ����� �������äƤ���ʪ���ˤ�ä��Ѳ����뤳�ȤϤ���ޤ��Ĥޤꡢ����������ñ����������������뤵�ϡ�����ʪ���β��٤����Ƿ�ޤäƤ���ΤǤ����������� �դ��ʤ���Ф����ʤ��Τϡ����٤ȴط��ʤ����ο��䶯�٤���ޤ��礬����Ȥ������ȤǤ������Ȥ��С���Τ褦�˸�������Ʃ���Ƹ������Τ��̤Ǥ������� ��ϡ��ɤΤ��餤Ʃ�������ޤ��������ɤ�ʸ������ͤ������ˤ�äơ����뤤�Ͽ��ˤ�äƤɤΤ��餤Ʃ���Ǥ��뤫��㤦�Τǡ����٤Ȥϴط��ʤ��������뤵�� �����ޤ����ޤ���ɽ�̤��̤ΤȤ��������褿����ȿ�ͤ��Ƥ���ʪ�����Ǥ������Ȥ��С����϶����Ȥβ��٤˴ط��ʤ����ɤ줯�餤�Τɤ�ʸ���ȿ�ͤ��Ƥ��뤫 �ǿ������뤵���Ѥ��ޤ��͡�����������ˤ��Ƥ���Τϡ�Ŵţ���ϤΤ褦�ʸ�����¦��Ʃ���Ƹ����ʤ�ʪ���ǡ�Ǯ���ʤäƼ�ʬ�ǵ����Ƥ����Τ����Ǥ����� �Τ褦�ʡ�������¦��Ʃ���Ƹ����ʤ�����ʬ�����ͤ��Ƥ���ʪ����������ͤϡ��������ͤȤ�Ф�ޤ���
���������ͤǤϡ�����в��٤��狼�ꡢñ�����Ѥ���������뤵����ޤäƤ��ޤ����顢�դ������뤵�Ȳ��٤�¬�ꤹ��С����äƤ������Ѥ�ջ����뤳�Ȥ��Ǥ��ޤ���
�������ޤǤϡ��Ļ���Ǥ��äΤ褦�˽Ƥ��ޤ����������������ξ�������Ʊ���Ǥ����Ļ���Dz��٤���ꤹ�뤿��˻Ȥ����ο��Ȥ����Τϡ�������Ĺʬ�� (���ͥ륮�����ڥ��ȥ�)�Τ��ȤǤ�����X������Ĺʬ��(���ͥ륮�����ڥ��ȥ�)��Ĵ�٤�С�X����Ф��Ƥ���ʪ�β��٤�ʬ����ޤ����⤷�����줬��X ���פǡ�Ʃ���Ƹ����ʤ���ʬ�ǵ����Ƥ����Τʤ顢ñ�����Ѥ�����˽ФƤ���X�������뤵�ϡ����β��٤ˤ�äƷ�äƤ��ޤ���
�����������⡢������¦��Ʃ���Ƹ�����ȤϹͤ��ˤ�����X���С����ȤΤۤȤ�ɤ�����������ɽ�����Τǵ�����ȹͤ����Ƥ���Τǡ�X���С����Ȥλ���ɽ�̲���(X���Υ��ͥ륮�����ڥ��ȥ�)�ȡ����Τ����뤵����Ƥ�����С�Ⱦ�¤���뤳�Ȥ��Ǥ��ޤ���
�����ζ���Ǥϡ������ٿޤ��Ѥ���Ⱦ�¤���ޤ���X��ŷ�ΤϹ������ͤ��Ƥ���Ȳ��ꤹ��ȡ�Ⱦ�¤Ȳ��٤���ޤ�п����ٿ��������ޤ�ޤ����ǡ����ȥ�ǥ����Ӥ��뤳�Ȥǡ�Ⱦ�¤���Ƥߤޤ��礦��
���������֤��ױ����Υǡ����Ƥߤ褦
�������̤β��¤������Ʊ���褦�˾�����Ϣ���Ϥǣ����С����Ȥ���ͭ̾��ŷ�Τǡ��أ��������ݣ������Ȥ���ŷ�ΤΥǡ������Ѥ��ޤ����֤��ױ����Ǽ������������Σأ��������ݣ������Ȥ��������С��������θ��ٶ�����ţأãţ̤Υ�������ȤȤ��ƽ��ǡ�����X1608-522_burst.xls�� �����ޤ���������å����ƥե������ɤ�������¸���Ƥ��������������ơ���¸���������Ƥߤޤ��礦��������ϡ������С����Ȥ�ޤ�����θ��ٶ����Υǡ��� �Ǥ��������Ȥβ��Υ��֤���[data]�ȤʤäƤ��뤳�Ȥ�Τ���Ƥ����������ʤäƤ��ʤ���С�[data]�Υ��֤�å����Ƥ���������
�����ٶ����Ȥϡ�����줿���ֳִ֡ʻ��֥ӥ�ȸƤӤޤ��ˤ˴�¬���줿���ҤθĿ���������ɽ��������դǤ�������Σţأãţ̤Υǡ����ϸ��ٶ�����������뤿��Τ�ΤǤ����ޤ��Ϥ��Υǡ��������ޤ��礦��
��A��ϡ��ƻ��֥ӥ���濴�����A�ԤΥǡ��������������������Ȥ���ɽ���Ƥ��ޤ���ñ�̤��äǤ���B���C��ϡ����ä�����˸��д郎���Ф������Ҥο���[photons/sec/m2]��ɽ���Ƥ��ޤ���B���C��Υǡ����ΰ㤤�ϡ����ͥ륮���ϰϤΰ㤤�Ǥ������Σ�����Υ��ͥ륮���ϰϤϡ�B�ԡ�C�Ԥ˽Ƥ���ޤ���
���������������ٶ����Υ���դ�������褦
�� ���ǡ���������ٶ����Υ���դ�������Ƥߤޤ��礦��
��A���X����B��C���Y���Ȥ�������դ���˽������Ƥ���ޤ��������Ȥβ��Υ���[X1608-522_LC]�Υ��֤�å����Ƥ������������������֤ǡ��ļ�������줿���ͥ륮���ϰϤˤ�äƤ������������������ꡢ���äο��Ǥ������Υ���դȥǡ������顢���������ն�Ǵ�¬���줿���Ҥο����������Ƥ��뤳�Ȥ��狼��ޤ���������ʬ��X���С����ȤǤ�������������Ⱦ�¤����ˤϡ����ΥС�������ʬ�Υǡ�����ɬ�פˤʤ�ޤ���
�����ơ����Υ���դ�褯����ȥС�������ʬ�ʳ��Ǥ⡢X�������Ф���Ƥ��뤳�Ȥ�ʬ����Ȼפ��ޤ�������ϣ������С����Ȥ����Ƥ��ʤ����Ǥ����ͤ� �Ƥ�����ʬ�Ǥ�����������ɽ�̤������ʬ�⤢�뤷����������ɽ�̰ʳ��ξ��ʤ��Ȥ��й�����סˤ������ʬ�⤢��ȹͤ����Ƥ��ޤ��������ʬ�ȸƤФ�� ���������С����Ȥλ��ˡ���������ɽ�̰ʳ�����ʬ�Ϥɤ��ʤäƤ���Τ��褯ʬ���äƤ��ʤ��ΤǤ����������Ǥϡ������ʬ�ϣ����С����Ȥλ�����٤����Ū �������Τǡ�̵�뤷�ơ������С����Ȼ��Σ����٤�������ɽ�̤���Σ����Ȳ��ꤷ�Ʋ��Ϥ�ʤ�ޤ��� ��
�����ꡡ5 X���С����ȤϻϤޤ꤫����綯�٤ˤʤ�ޤDz��ä����äƤ���Ǥ��礦��������դΣ����С����ȤΤ��������礹��Ȥ褤�Ǥ��͡�
�������������ٿ�
�������ٿޤȤϡ����ٶ������㥨�ͥ륮���ϰ�(0.75��7.9keV)�ȹ⥨�ͥ륮���ϰ�(7.9��12.2keV)�Ǥθ��ҿ�����Ψ��ļ��ˡ����ҿ��ι�פ���ɽ��������դǤ������ͥ륮���ϰϤΰ㤦�Ȥ����Ǥθ��ҿ�����Ͽ����б�����Ȥ����櫓�Ǥ���
���ޤ��ϡ������ٿޤ�X����Y�����ͤ�����ޤ��礦�������ٿޤ�X���������� �륮���ϰϤΥ�����ȿ��ι�ס�Y���ϡ��㥨�ͥ륮���ϰ�(0.75��7.9keV)�ȹ� ���ͥ륮���ϰ�(7.9��12.2keV)�ǤΥ�����ȿ�����Ψ�Ȥ��ޤ���D��˥������ ���ι�ס�E����㥨�ͥ륮���ϰ�(0.75��7.9keV)�ȹ⥨�ͥ륮���ϰ�(7.9�� 12.2keV)�ǤΥ�����ȿ�����Ψ������Ƥߤޤ��礦���ޤ��ϡ������Ȥβ��Υ� �֡�[data]��å����ơ��ǡ����Υ����Ȥˤ�ɤ�ޤ���
����D�Ԥˡ���=B4+C4 ���Ǥ�����Ǥ�����������������С���ĤΥХ�ɤι�פ��Ǥ��ޤ���
����E�Ԥˤϡ�=C4/B4 ���Ǥ�����Ǥ���������������椬�Ǥ��ޤ���
�������ˤ���D��4�Ԥ�E�Ԥ�D���E���5���ܰʹߤιԤ˥��ԡ����Ƥ������������Ƥλ���ι�פ��椬���Ǥ��ޤ���
�������������Ƥ��ȤȤ��ƽƤ����ޤ��礦��D�Ԥˡ��֣����С����Ȥζ��١ס�D�Ԥ��ܤˡ����ͥ륮���ϰϤȤ��ơ���0.75-12.2
keV�ס����줫�顡D���ܤˡ�ñ�̡�Photons/sec/�����פ���ߤޤ��礦��E���ܤˤϿ���E���ܤˤϡ�I(7.9-12.2keV)/I(0.75-7.9keV)�פȽޤ��礦��E���ܤ��ä˽��ȤϤʤ��Ǥ��͡�����ˤ�ñ�̤Ϥ���ޤ���
����D���ؼ��������ټ��Ȥ��ƻ��ۿޤ��äƤ�������������������Υ���ե��������ɤ�ȤäƼ�ʬ�Ǥ�äƤߤƤ�������������դΥ����ȥ�ˤϡֿ����ٿޡס��ؿ��ͼ��ˤϡ֣�(0.75-12.2
keV)��, X���ͼ��ˤϡ�I(7.9-12.2 keV)/I(0.75-7.9keV)�פȽƲ��Υ���դ�ʬ����褦�ˤ��Ʋ�������
�� ��ä�����դ��̤Υ����Ȥˤ��Ʋ�������̾�����Intensity-Color Diagram�פȤ�����ɤ��Ǥ���[Intensity-��olor
��iagram]�Υ��֤��Ǥ��Ƥ��줬ɽ������ޤ����ؼ��ζ��٤��礭���ʤäƤ���Ȥ����������С����ȤΤȤ����Ǥ������١ʣؼ��ˤ����äȤȤ�˿��ʣټ��ˤ��礭���ʤäƤ��뤳�Ȥ�ʬ����ޤ���
����������������ļ��ϥ�˥�ˤ���ȸ��䤹�����ˤʤ�ޤ���������100���飱�ţ����ޤǤˤ���ȥǡ��������礦������ޤ����ļ���0���飰�����Ǥ褤�Ǥ��͡�
�� �����ο��Ȥ����ͤϡ������ΰ�β��٤ȴ�Ϣ���ޤ��������С����Ȥϡ�����������ɽ�̤ǡָ�����¦��Ʃ���Ƹ����ʤ���ʬ�Ǹ���ʪ���פ�������ͤȹͤ��Ƥ褤 ��ΤǤ����Ǥ����顢�������ͤȹͤ��Ƥ褤�Ǥ��礦������դο��ʣټ��ˤϡ����ͥ륮���ι⤤��������Ĺ��û�������ˤζ��٤ͥ륮�����㤤��������Ĺ ��Ĺ�������ˤdz�ä���ΤǤ������ʤ������Ĺ��û���������ɤ줯�餤¿���ޤޤ�뤫���̣���Ƥ��ޤ�����Ĺ��û���Ȥ����Τϡ��Ļ�����ΰ�Ǥ��Ŀ����� Ĺ��Ĺ���Ȥ����Τ��֤����Ȥ��̣���ޤ������ʤ���ټ��ϡ������ο��Τ褦�ʳ�ǰ��ɽ���Ƥ��ޤ����������ͤǿ��Ȥ����Τϲ��٤����Ƿ�ޤ�ޤ��������� �ʣؼ��ˤϡ����٤���ޤ�С����ͤ��Ƥ����ΰ�����Ѥ��礭������礭���ۤɶ��٤������ʤ�Τǡ��դˡ����٤��������ΰ�����Ѥ������ޤ���
������������������
���ǡ�������������ͤȲ��ꤷ�����β��٤����Ѥ���ޤ��礦�����������ΰ���ٰ���ε�Ȳ��ꤷ�����β��٤ȡ����Ⱦ�¡����줫�顢�����ΰ�� �Ǥε�Υ�Ⲿ�ꤷ�������ɤΤ褦�ʥǡ��������ԤǤ��뤫���ǥ�����Ƥߤޤ����������ͤβ��٤�Ϳ�����ñ�����Ѥ����ꡢñ�̥��ͥ륮�������ꡢñ��Ω �γѤ�������ż��Ȥι������ͤȤ������ͤ������Ҥο�ʬ�ۤͥ륮���˴ؤ��뼰��ɽ�����Ȥ��Ǥ��ޤ����������ץ��ʬ�ۤȸƤӤޤ��� �����ˡ�����������Ⱦ�¤��ꤷ���ޤ����������������¬���Ƥ���������ޤǤε�Υ�Ⲿ�ꤹ��ȡ���¬���Ƥ����ˤ�äƤ��롢ñ�����ѡ������������ ���ҿ��ο�ʬ�ۤ�ʬ����ޤ��������ơ���¬���Ƥ��륨�ͥ륮���ϰϤ�Ʊ�����ͥ륮���ϰϤδ֤���(��ʬ�ˤ����ͽ�ۤ������ҿ���ʬ����ޤ����ܤ����� �������Ӥ���ޤ��Τǡ�������å������ٶ����ƤߤƤ���������
�� ����¬�ˤ��碌����ĤΥ��ͥ륮���ϰϤǸ��ҿ����ᡢ���Ρ���פ�������С������ٿޤ���������ǤĤ��Ȥ��Ǥ��ޤ������������ʲ��١�����������Ⱦ �¡�ŷ�Τȿ������ε�Υ���ꤷ�Ƥ�뤳�Ȥǡ������ٿ�ˤ��������������ǤĤ��Ȥ��Ǥ��ޤ�������ǡ��֤��ױ����Ǹ��Ф����ǡ�������ӤǤ��뤳 �Ȥˤʤ�ޤ���
�����������������ͥ�ǥ�η�
�� ����Ǥϼºݤˣţأãţ̤Ƿ����Ƥߤޤ��礦�����Τ���ˤϹ������ͥ�ǥ�˻Ȥ��Ƥ��뤤��������ʪ�������ñ�̤�·�����ꤷ�ޤ�������ϡ���������������ޤ�������å������ٶ����ƤߤƤ����������ǽ�Ū�ˤϡ��������ͤΥ�ǥ��
![]()
�ǡ����Ǥ��ޤ������Ѥ���ñ�̤ϡ����ҤΥ��ͥ륮����![]() �ˤⲹ�١�
�ˤⲹ�١�![]() �ˤ⡡keV �Ǥ�������ǡ����벹�٤λ��ι������ͤȤ������ͤ������Ҥο���ʬ�ۤȤ����櫓�Ǥ���
�ˤ⡡keV �Ǥ�������ǡ����벹�٤λ��ι������ͤȤ������ͤ������Ҥο���ʬ�ۤȤ����櫓�Ǥ���
�������ǡ�������Ӥ���ˤϡ�����������Ⱦ��![]() �ȡ����������ޤǤε�Υ
�ȡ����������ޤǤε�Υ![]() ��ɬ�פǤ�����¬�������Ҥο�ʬ�ۤ�
��ɬ�פǤ�����¬�������Ҥο�ʬ�ۤ�
![]()
�Ȥʤ�ޤ���
�����̤�ŷ�Τε�Υ�����Τ�¬�ꤹ�뤳�Ȥ��������ơ��������Ѥ���ŷ�Ρ�X1608-522�ε�Υ���Գ��������礭���Ǥ�������ϡ�X1608-522�ޤǤε�Υ��8[kpc]�Ȥ��ޤ���![]() �ʤΤǡ�
�ʤΤǡ�
![]()
�Ȥʤ�ޤ�������ǡ��������ͥ�ǥ���������������Ǥ��ޤ�����
�ޤ���BlackBody.xls�� ����EXCEL�Υե������å����Ƥɤ�������¸���Ƥ��������������ơ���¸�����ե�������Ƥߤޤ��礦�������Υ��֤���[��ata]�ȤʤäƤ� �뤳�Ȥ�Τ���Ƥ����������ʤäƤ��ʤ���С�[��ata]�Υ��֤�å����Ƥ����������Ϥ���Σ����ԤϷ����뤿��Υѥ�������ǽ�Ū�˵� ��̤�������Ǥ����������ܤ��鲼���������ͤη��뤿�����Ǥ�������Σ������ܤ��鲼�Ϸ����륨�ͥ륮���ϰϤ��濴�͡�����Σ������ܤ��鲼 �ϡ����줾��Υ��ͥ륮���ϰϤ�����ޤ����������Ǥϥ�ǥ���ʤΤǡ��ºݤΡ֤��פΥǡ�������٤ơ����٤������ޤ������ΤΥ��ͥ륮���ϰ� ��������ޤ��������걦���������ͤη��ͤǤ������������������ͤβ��٤ȡ���Υ���ܤȣ����ܤ˽ޤ����������ܤϣ����ñ�̤˽� �Ƥ���Τǡ������ܤǣ��˴���������Υ������ޤ��������ܤ������ΰ��Ⱦ�¤�[m]��ñ�̤˽Ƥ��ޤ������ʤ��������ϵ�Υ��kpc�ˤ��롢���� 1.0keV��Ⱦ�£�km�ε夫�����ͤ����������ͤΥ��ͥ륮�����Ф��붯���ʥ��ͥ륮�����ڥ��ȥ�ˤ�����褦�Ȥ����櫓�Ǥ���
�����ޤ������Ԥ���ȤƤߤޤ��礦��
������=9.87E+35*$A13^2/(EXP($A13/C$1)-1)*(C$4/C$3)^2*$B13
���������äƤ���Ϥ��Ǥ������٤�C�𣱤ǵ��Τ�Ⱦ�¤�C$3��ŷ�ΤޤǤε�Υ����C$���ξ��Υ��ͥ륮����A13�ǡ������������ꡢ���ͥ륮���ӥ����ʺ��ξ��$B13�ʤΤ�0.2keV)�����ꡢ���äδ�¬�������Ҥο���ɽ���Ƥ��ޤ���ñ�̤�
[photons/sec/m2]�Ǥ�����C���15���ܰʹߤ�Ʊ���褦�ʷ��������äƤ��ޤ���
������C��6���ܤƤ���������
������=SUM(C16:C51)
���ȽƤ���Ǥ��礦�������C16����C51�ޤǤι�פǤ����顢0.8keV����7.8keV�δ֤Υ��ͥ륮���ϰϤǣ��������������ô�¬�������Ҥο��Ȥ����櫓�Ǥ���
��Ʊ�ͤ�C��7���ܤ��
������=SUM(C52:C73)
�ȽƤ���Ϥ��Ǥ�������ϡ�8.0keV���顢12.2keV�δ֤Υ��ͥ륮���ϰϤǣ��������������ô�¬�������Ҥο��Ǥ��� �������ơ�C��9���ܤǤϡ�C��6���ܤ�C��7���ܤ��¡�C��10���ܤˤ����Ƥ���ޤ��������ο����ǡ������ٿޤ�Ф褤�櫓�Ǥ���
���Ǥϡ�¾�β��٤�Ⱦ�¤Ǥ�����Ƹ��ޤ��礦���ʤ��������Ǥϵ�Υ�Ϥ��Ĥ⣸kpc�ȸ��ꤷ�Ƥ������Ȥˤ��ޤ��礦���ʤ���D��E��ˤϡ����Ǥˡ�1.5
keV, 2.0 keV �ξ��η��Ƥ���ޤ���
�����������Τ���˥��ԡ����Ƥ��������������ܤβ��٤�, 2.0 keV����,
2.5 keV���ѹ�����С���2.5 keV�Υ��ͥ륮�����ڥ��ȥ뤬����夬��ޤ���
�����ޤǤǡ���Υ��Ʊ����8����ˤȤ����ˤ��롢Ⱦ��2��������(2���)�ε夫�����ͤ���롢���٤� 1.0, 1.5, 2.0, 2.5keV�ι������ͤΥ��ͥ륮�����ڥ��ȥ뤬���Ǥ��ޤ�����
���������ˣ���Υ��ͥ륮�����ļ��ˣ������ޤǤΥ��ͥ륮�����ڥ��ȥ�Ȥ�������դ�ƤߤƤ���������
�¤ϡ����Υ��֤�[��������]��å����ƤߤƤ���������ξ�п��ǽ���keV
�ȡ�1.5 keV �Υ���դ�����ޤ������Υ���դͤˤ��ƽƤߤƤ���������
���ޤ��ϡ��ġ���С��Υ���դ��顢���Υǡ��������ӡ�����Ρ֡��ңţơ��פ����ơ�̾���ˤ�
����=data!$E$1
���٤���(Y) �ˤ�
����=data!$E$13:$E$209
����ˡ��⤦��Ĥ�#REF! ������ǡ�Ʊ���褦�ˣ����Ѥ˽����ޤ��礦��
���οޤΤ褦�ˤʤ�Ǥ��礦��
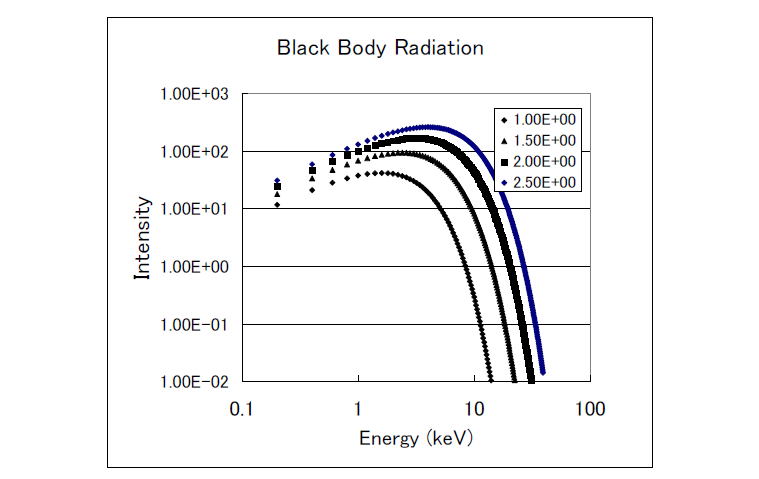
�ͤι⤤��Τ��顢2.5 keV, 2,0 keV, 1.5 keV,1.0 keV �Ǥ���
�����ꡡ6 �������ͤΥ��ڥ��ȥ����ħ��äƤ���������
���դ����ӡ����Υ��֤Ρ֣ģ����פ�å����ơ��ǡ����Υ����Ȥ�ɽ�����Ƥ������������ޤǤˡ����Ⱦ�¤�2km�Dz��٤��㤦�������ͤΥ��ڥ��ȥ������ޤ�������
�����������ԡ����ơ�Ⱦ�¤���4�����8�����16�����32����ξ��Τ��줾��ξ��ǡ����٤�1.0, 1.5, 2.0, 2.5keV���ξ�������Ƥ���������4����˥��ԡ�����ȳڤǤ��͡�
����ǡ�Ⱦ��2����η���ޤ�ơ�Ⱦ�£��Ȥ��ꡢ���٣��̤ꡢ�ǹ��2���̤�η����Ǥ��ޤ�����
�����������������ͥ�ǥ�ˤ�뿧���ٿ�
�����褤��ǡ�������Ӥ��뤿�ᡢ�������ͤΥ��ͥ륮�����ڥ��ȥ뤫�鿧���ٿޤΥ���դ��äƤߤޤ��礦���¤ϥǡ����Υ����ȤΣ����ܤȣ����ܤ�0.8keV���飱������keV�θ��� ����ʿ��� ����ޤäƤ��ޤ������������ʲ��٤�Ⱦ�¤��ͤ�������V��ˤ�����Ǥ��Ƥ���Ϥ��Ǥ���
������Ǥϡ� �����ٿ� ��Ƥߤޤ��礦��
������������դˤ������ΰ�Ǥ��롢�ã�����V�����ޤǤ��ΰ�����ޤ���
������������ե��������ɤǻ��ۿޤ����ޤ���
�����������Ȥϡ�����ե����ȥ�ˡֹ������ͤο����ٿޡס��ؼ��Υ����ȥ�ˡָ��١�(0.8-12.2
keV)�ס��ټ������ȥ�ˡֿ����ɡ�8.0-12.2keV)/I(0.8-7.8 keV)�ס��Τ褦�ˡ������ȥ��Ĥ��Ƥ���������
��������������������ļ��ϥ�˥�ˤ���ȸ��䤹�����ˤʤ�ޤ���������100���飱�ţ����ޤǤˤ���ȥǡ��������礦������ޤ����ļ���0���飰�����Ǥ褤�Ǥ��͡�
�Ǥ�������դϡ����Υ��ֹ֡������ͤο����ٿޡס�����¸���Ƥ����������Ǥ⡢����դ������ȡ��ɤ��������������Ǥ����ɤ��������Υǡ��������Τ���Ƹ��ޤ��礦��
���ǡ�������ʤ����ȡ�5�ܤα��夬��Υ����֤ȸ��뤳�Ȥ��Ǥ��ޤ������Υ����֤��顢���줾�졢Ⱦ�¤� 2km,4km,8km 16km 32km���б����ޤ����ޤ������줾��Υ����֤δޤޤ�룴�Ĥ����ϲ����顢���٤�1.0keV, 1.5keV, 2.0keV, 2.5keV���б����ޤ���
���������ǡ����ȹ������ͥ�ǥ�����
���ǡ��������ä������ٿޤȡ��������ͤΥ�ǥ뤫���ä������ٿޤ���Ӥ���ȡ�����������Ⱦ�¤䲹�٤��Ф�Ϥ��Ǥ�����ĤΥ���դ���٤Ƹ��ޤ��礦���ǡ����ϥС����Ȼ��ˤϸ��٤ϡ�����104 photons/sec/m2�� �٤ǿ���0.25��0.3�δ����٤Ǥ�������������ͤΥ�ǥ뤫������������ٿޤǤϡ�Ⱦ�¤�8km���٤ǡ����٤�1.5keV���٤Ȥ������Ȥ��� ����ޤ��� ��äȾܤ�������ȡ��С����Ȱʳ��ΤȤ����ϡ�Ⱦ�£�����4��������٤���.0keV������ǡ��С����Ȥ��Ϥޤ�ȡ����Ѥ��������礭���ʤ�ʤ��顢���� �⤢���ꡢ�䤬�Ʋ��٤��䤨�Ƥ��뤳�Ȥ�ʬ����ޤ����Ǥ⡢�С����Ȱʳ��ΤȤ����Ǥϡ���������ɽ�̤�������ǤϤʤ����㤦�Ȥ��������X���⤢�뤫�⤷ ��ޤ����������ͤ�Ȥ��Ȥ��������褯�ʤ����Ȥ�ʬ���äƤ���Τǡ����ޤꡢ�٤��������ˤ�����äƤϤ����ޤ���
������ǡ��֤��ױ�������¬�����ǡ�����������������Ⱦ�¤ˤĤ��Ƥξ�����Τ뤳�Ȥ��Ǥ��ޤ������Ǥ⡢�����ǤϤ����Ĥ��β���Ƥ��ޤ���
������������X1608-�������ޤǤε�Υ��8kpc
�����������С����Ȥϵ��������������ɽ�����Τ�������Ū�����ͤ���Ƥ���
�����������С����Ȼ��Σ������ͥ륮�����ڥ��ȥ�Ϲ������ͤǤ���
�����������ʬ�θ��̤�ͤ��Ƥ��ʤ�
�Ȥ��Ǥ�����Υ���Գ������ϡ����餫����ˡ�Dz�褹��ɬ�פ�����ޤ�������¾�β�������٤ι⤤�������ϡ��Խ�ʬ�Ǥ��뤳�Ȥ�ʬ���äƤ��ޤ������� ���ʤ��顢�����ǹԤä��褦���绨�Ĥʷ��Ǥ⡢��Υ���������ʳ��ϲ��ܤ��礭���ְ㤦���ȤϤ���ޤ��ޤ�����Υ�⺣�ΤȤ������ܤ�ְ�äƤ��ʤ��� �פ��ޤ��Τǡ�Ⱦ�¤⣲�����ٰ���ǤϤ��äƤ���Ȼפ��ޤ������ä�����������Ⱦ�¤Ͽ�������齽������Ǥ��뤳�Ȥ��狼��ޤ���
������������
���ζ���Ǥϡ����������ȹͤ����Ƥ���X1��08-52�Ȥ���ŷ�Τμ��̤�Ⱦ�¤���Ƥߤޤ��������̤��� ����ϡ������֤�X���Υե�å�����Ȥ��ޤ������Ǥ⡢����ŷ�Τ�X���С����Ȥ����Ƥ�ä����뤯�ʤ�櫓�Ǥ��͡��Ǥϡ�X���С����Ȥλ������뤵 ��Ȥ��С���ä������˶ᤤ���̤�������ȹͤ����ޤ������ζ���Ǥϡ�X���С����ȤΥǡ�����2�Х�ɤΥǡ�����������ޤ��������ȤäƤ�Ʊ ���ͤ˥ե�å����ζ���ͤϷ��Ǥ��ޤ����������ơ����̤Τ褤�����ͤ���ƤߤƤ���������
������ˡ��أ��������ݣ��������Ȥ����̤Σ����С��������Σ����С����ȤΥǡ�����������ޤ������أ��������ݣ������ε�Υ�⽼ʬ��ʬ���äƤ��ޤ���
��Ϥ꣸�������٤ȹͤ����Ƥ��ޤ������ͥ륮���ϰϤ�Ʊ���Ǥʤ��Τǡ��������ͤη���ǡ����ˤ��碌�ƿ����ٿޤ���ľ���ʤ��Ȥ����ޤ���Ʊ��
�褦��Ⱦ�¤��������Ǥ��ޤ������������С����Ȥλ���ʪ���������Ǥ�������ʲ��٤�������Ⱦ�¤����礹�븽�ݡˤ�ʬ����ʪ�⤢��ޤ���
����ĩ�路�ƤߤƤ���������
��X1636-536_No1
��X1636-536_No2
��X1636-536_No3
��X1636-536_No4
![]()
����ΤޤȤ������
��
����1
����ñ�̤Ϥɤ��ʤ�Ǥ��礦�������� �����������ͥ륮���ϡ�����2/s2 �ǡ�®�٤�m/s�������顢����/s���Ȥʤꡢ��ư�̤�ñ�̤Ǥ��롣
����2
���ꣲ�������ܤΥХ�ɤΥ��ͥ륮���ϰϤϤɤ�����ɤ��ޤǤǤ�������������������������������keV�����顡������keV
����3
���ꣳ�������٤�ñ�̤Ϥɤ��ʤ�Ǥ��礦�������������� ������J/sec �ޤ��ϡ�����
����4
���ꣴ:�������������μ��̤����ۼ��̤���ӤƤߤޤ��礦�����ۼ���Mo�� Mo=1.99��1030 [kg]���Ǥ�������������������
����5
���ꣵ��X���С����ȤϻϤޤ꤫����綯�٤ˤʤ�ޤDz��ä����äƤ���Ǥ��礦������������������դΣ����С����ȤΤ��������礹��ȸ��䤹���Ǥ��͡��ޤ�������դβ����ο�������֥륯��å����Ʋ����������ν�����Ȥ���������� �����ФƤ��ޤ�������֤�å�����ȡ������κǾ��͡������ͤ����ϤǤ��ޤ���100���飳�����Ȥ���ȡ��С��������Τ�����00����130�Ȥ��� �ȡ�Ω���夬�꤬�褯�����ޤ���
��������������������6�äǤ����Ǥ�3�����٤Ǹ������뤵��10�����٤ˤʤäƤޤ������Τ褦�ˤ��ʤ��ᤤ���֤Ƕ��٤���ư���뤳�Ȥ��顢X���Ͼ������ΰ�����ͤ���Ƥ��뤳�Ȥ�ʬ����ޤ���
����6
���ꣶ�������ͤΥ��ڥ��ȥ����ħ��äƤ�����������������������
��1. ���줾��Υ���դϡ���äȤ�⤤�ԡ��������롣
�������ԡ����Υ��ͥ륮���ϲ��٤��⤤�ۤ��礭���ʤ롣
������Ʊ�����ͥ륮���ΤȤ����ǡ����٤��⤤�ۤ����뤯�ʤ롣
�������ԡ��������㤤���ͥ륮���ΰ�Ǥϡ�ξ�п��ǽȡ����ͥ륮�����Ф��Ƥۤ�ľ��Ū�����뤯�ʤ롣
�������ԡ������⤤���ͥ륮���ΰ�Ǥϡ�ξ�п��ǽȡ��㤤�Ȥ��������ä�������ꡢ��˸������롣
���Τ��Ȥ�������Ǥ��礦�����Τۤ��ˤⵤ���դ������Ȥ����뤫���Τ�ޤ���͡�