見えない天体ブラックホールを見る
1. はじめに
SFなどにブラックホールというものがよく登場する。「こんなの本当に存在するの?」と疑問に思った人も多いのではないだろうか。
実はブラックホールの候補天体はいくつか発見されている。
天文学では一体どのようにブラックホールを扱っているのだろうか?
1.1 ブラックホールって何だろう?
ブラックホールときいて、どういうものを想像するであろうか。宇宙に空いた小さな穴?何でも吸い込んでしまう恐ろしい空間?
答えをひとことで言ってしまえば、「光でも逃げ出せない星」である。
ボールを上に投げると、ある高さまで上がる。
ボールのスピードを速くすると、もっと高い場所まで上がるだろう。
ではもっともっと速くするとどうなるだろうか。
地上から秒速11.2km(時速4万km!)の速度でボールを上に投げると、地球の重力を振り切って、もう戻ってこない。
重力を振り切るのに必要な速度を脱出速度という。脱出速度は星の質量と半径で決まる。
星が重ければ重いほど、小さければ小さいほど脱出速度は大きくなる。
では脱出速度が光速を超えてしまったらどうなるだろうか?
何者も光速以上の速度は出せないので、その星からの脱出は不可能になってしまう。
ブラックホールとは、そういう星を指すのだ。
******チェック1. 地球の脱出速度を計算で出してみよう。******難易度 ... 中
1.2 どうやってブラックホールは作られるのか?
太陽と同じ重さのものを半径3km以下に縮めると、脱出速度が光速を超える。つまりブラックホールになる。しかし太陽は半径70万kmもある。そんなに縮めることが可能なのだろうか?
実は太陽をブラックホールにすることはとても難しい。無理だといってもいいだろう。
ただし、太陽の30倍以上重い星なら可能である。
太陽より何倍も重い星は、燃料を使い果たすと大爆発を起こすことがある。
この爆発によって星内部が圧縮され、ブラックホールと呼べるくらい小さく押し縮められるのである。
ブラックホールとは言わば星の残骸である。
ただの星ではない。「太陽の30倍以上もある、とんでもなく重い星」の残骸だ。
ちなみに天文学では、物理量の基準を太陽にする傾向がある。
質量もそうだ。だからブラックホールも「太陽の何倍の質量」なんて表現したりする。
いちいち太陽の何倍、なんていうのは大変なので、これから太陽の質量を Msun と書くことにしよう。
太陽の30倍の質量の星は「30Msunの星」と表現される。
1.3 ブラックホールは本当に存在するのか? - X線天文学とブラックホール候補天体の発見
これまで説明してきたブラックホール、理屈はいいが、本当に存在するかどうかは別の問題である。本当に「光でも逃げ出せない星」なんてものが存在するのだろうか?
この問いかけに、1970年代に発達したX線天文学という分野があるひとつの解答を出した。
1971年、日本のX線天文学の祖・小田稔によって、ついにブラックホールらしき天体が発見されたのである。
"それ"ははくちょう座の方向から強烈なX線を出しており、短い時間(約0.073秒)で激しく変動していた。
強烈なX線は莫大なエネルギーを意味し、激しい変動は小さい領域を意味している。
小さい領域からの莫大なエネルギー放射、これは太陽のような普通の星(恒星)ではあり得ない現象であり、
ブラックホールが現実に存在するかもしれない初めての証拠となったのだ。
現在この天体は、はくちょう座(Cygnus)に発見された1つ目のX線天体という意味で、Cyg X-1 (シグナス エックスワン)と呼ばれている。
ところで疑問が残る。
X線とは光(電磁波)の一種のはずだ。
なぜそんなものが「光でも逃げ出せない星」から出てくるのだろうか? 考えてみれば妙な話である。
実はこのX線はブラックホールそのものから出ているわけではなく、ブラックホールのごく近くから放射されているのだ。
詳しくは2章「X線を出すところ:降着円盤」を参照してほしい。
1.4 ブラックホールとペアになっている恒星を探す
1.3節で「X線はブラックホールのごく近くから放射されている」と書いたが、実はブラックホールが単独で存在する場合、そのようなX線は発生しない。
ブラックホールの近くからX線が放射されるためには、「ブラックホールと太陽のような恒星がペアになっている」という条件が必要なのである。
なぜペアである必要があるのか? それは2章で述べるので、ここではそういうものだと思ってもらいたい。
このように2つの星がペアになっているシステムを連星系と呼ぶ。
連星系にある星達は、システムの重心の周りをくるくる回る。
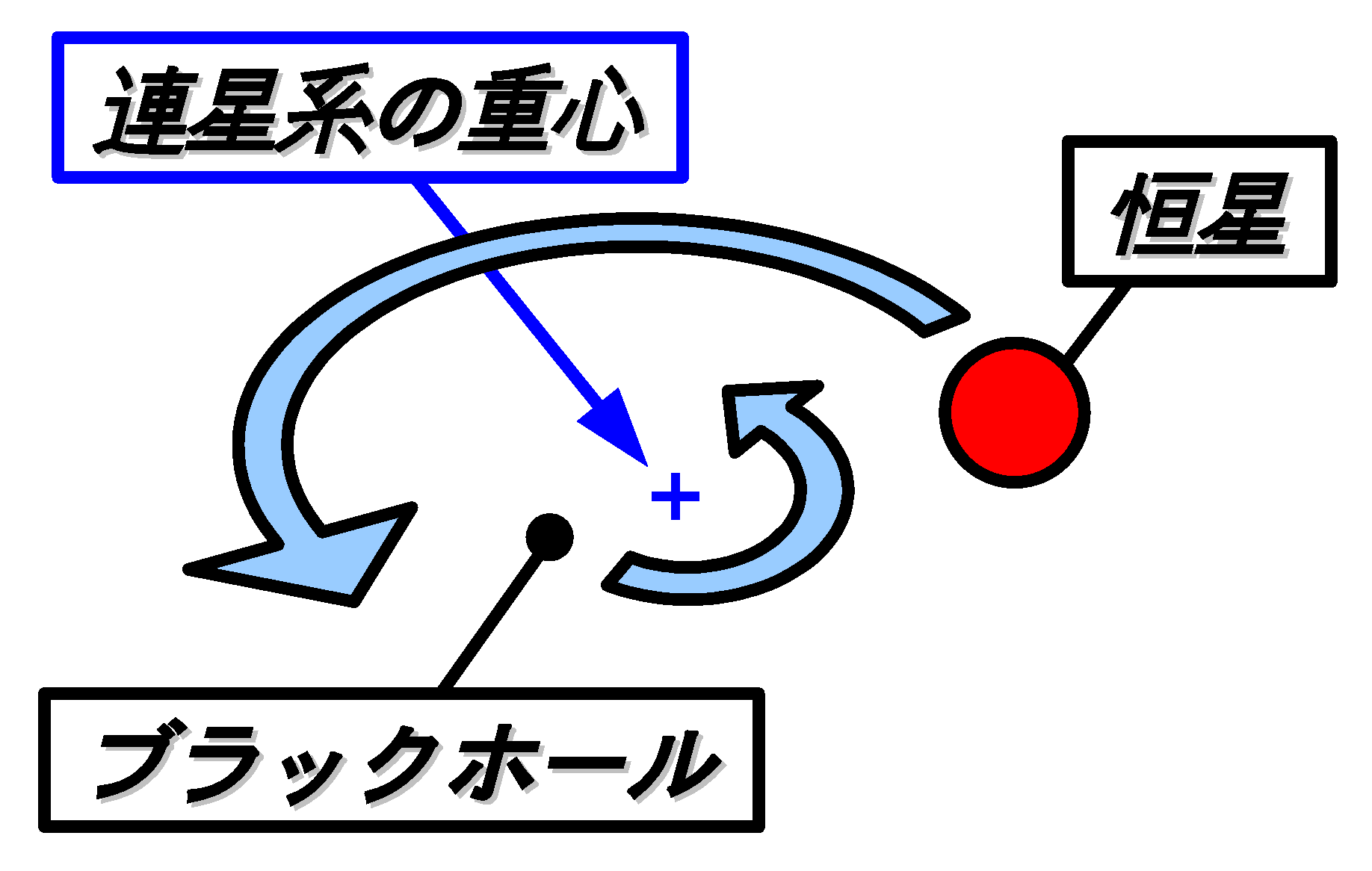
さて、ではさきほど紹介した Cyg X-1 も連星系になっているのだろうか?
ペアの星は太陽のような恒星であるから、目で見える光(可視光線)を出しているはずである。
つまり Cyg X-1 が発見された場所を可視光線で見てみれば、ペアの恒星が発見できるに違いない。

これは Cyg X-1 を可視光線とX線で見た画像である。
X線でひとつだけ強く輝いているもの、これが Cyg X-1 だ。
対して可視光線ではたくさんの星々があるが、真ん中にはひときわ輝く星が存在する。
これがペアの恒星である。確かにこのブラックホールにはペアの恒星が存在するようだ。
1.5 質量の見積り方
ところで、ペアの恒星がどれくらいの周期・速度で回っているのかを調べると、Cyg X-1 がどれくらい重いのか推測することができる。現在では Cyg X-1 は約10Msunであることが分かっている。
小さい領域に太陽の10倍もの質量が集中できるのは、ブラックホール以外に考えられない。
このように、ペアの動きからも Cyg X-1 がブラックホールであることが示唆されている。
******チェック2. ブラックホールの質量を推測してみよう。******難易度 ... 難
さらっと「ブラックホール以外に考えられない」と書いたが、なぜだか分かるだろうか?
小さい領域に質量が集中していている天体をコンパクト星と呼び、コンパクト星には3種類しかない。
白色矮星、中性子星、ブラックホールである。
このうち、白色矮星と中性子星には「これ以上重くなれない」という限界の質量があるのである。
白色矮星は約1.4Msun、中性子星は正確には分かっていないが約3Msunが限界だろうとされている。
一方でブラックホールには質量の限界がない。
つまり10Msunもの質量を説明するには、ブラックホール以外考えられないのである。
2. X線を出すところ:降着円盤
2.1 X線が出てくる仕組み
確かにブラックホールがある(と思われる)方向からX線が来ていることが分かった。しかしブラックホールは「光でも逃げ出せない星」である。
一体どこからこんなX線が出てくるのだろうか?
観測している対象が連星系であったことを思い出そう。
ブラックホールはペアである恒星のガスを剥ぎ取ることができる。
そのガスはまっすぐにブラックホールには向かわず、ブラックホールの周りを回転するようにゆっくりとブラックホールへ向かっていく。
すると円盤が形成され、その円盤は1千万度近くまで熱くなるのである。
この円盤を「降着円盤」と呼んでいる。
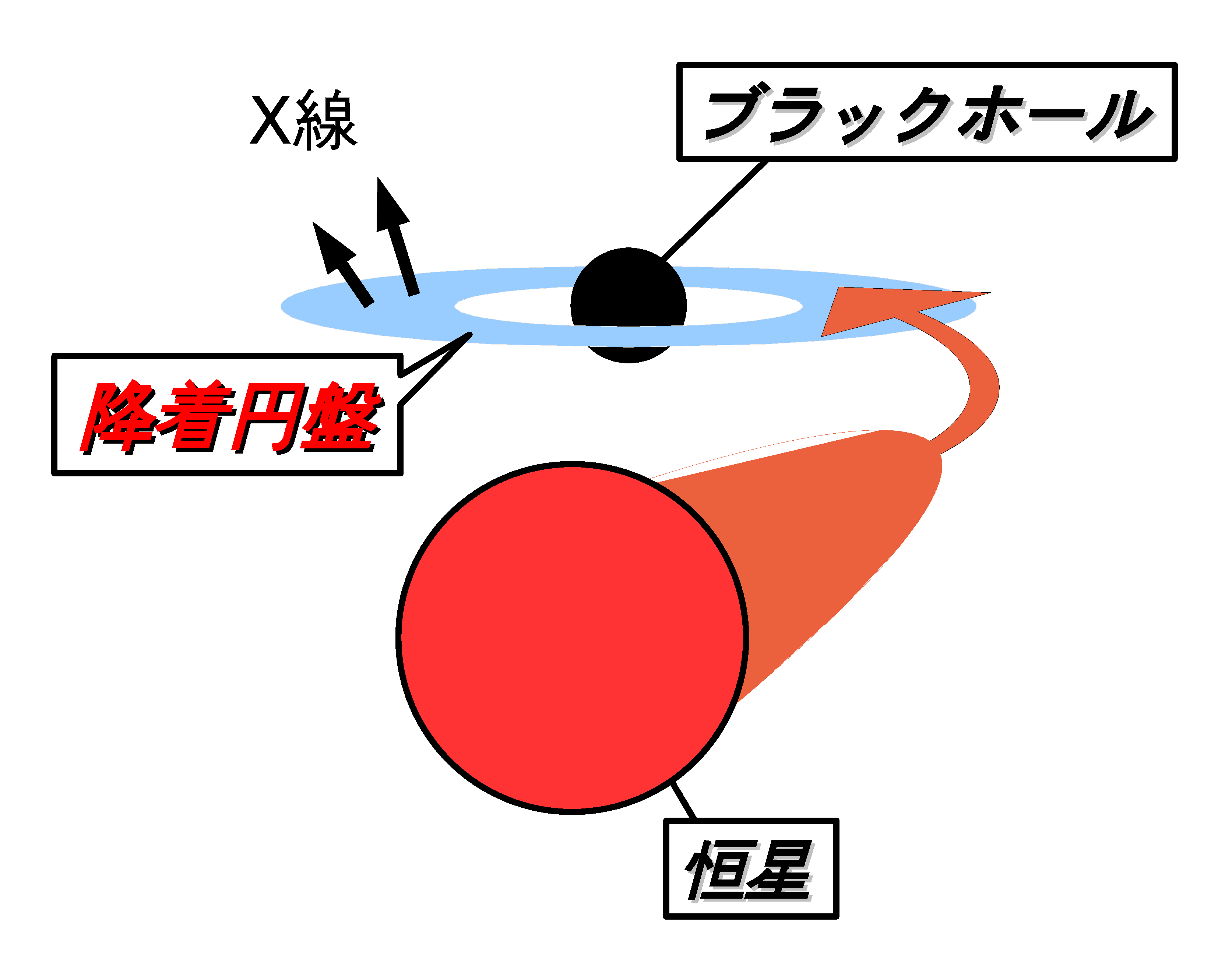
鉄を熱すると光輝くように、物質は熱くなると光を出すようになる。
1000度くらいでは可視光線しかでないが、1千万度くらいになるとX線を放出する。
我々が見ているX線は、ブラックホールの周りに形成された降着円盤からのものだったのだ。
ちなみにブラックホールと似たような天体・中性子星には、降着円盤からの放射にプラスして中性子星表面からの放射もある。
しかしブラックホールには降着円盤からの放射しかないのだ。これが両者の決定的な違いであると言える。
実際の研究でも、この違いが重要になることが多々ある。
2.2 ブラックホール特有の性質
2.1節でも触れたように、降着円盤は中性子星でも形成される。ブラックホール特有の円盤の要素は何かないだろうか?
降着円盤のイラストをよく見てみよう。ブラックホールと降着円盤の間に空間があるのが分かるだろうか。
実は降着円盤は、(ブラックホールが回転していない場合)ブラックホール半径の3倍までしか接近できないのである。
ブラックホール半径のことを「シュバルツシルト半径」と呼び、ブラックホールから円盤の一番内側までの距離のことを「内縁半径」と呼ぶ。
この性質は非常に使えそうだ。
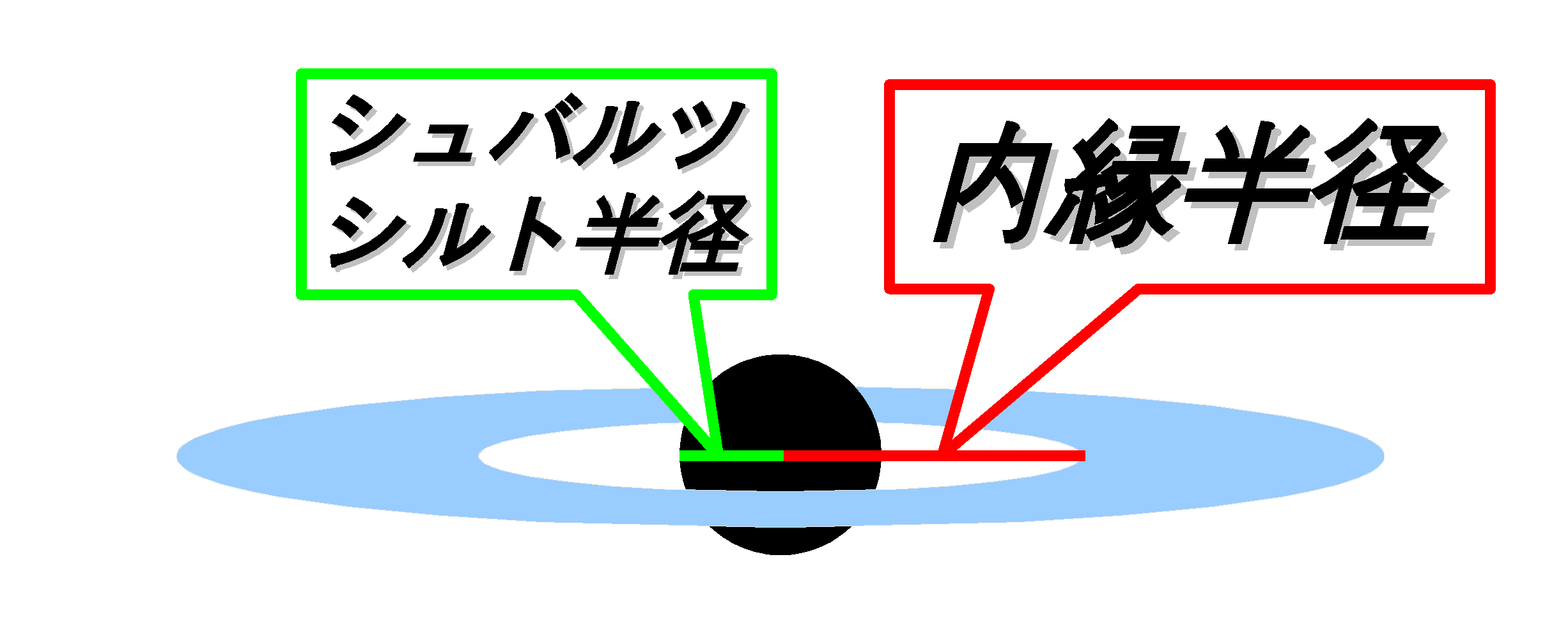
しかしなぜこんな内縁半径なんてものがあるのだろうか?
単純に考えると、円盤はシュバルツシルト半径まで接近できる気がする。
その原因は、ブラックホールがあまりにも強大な重力を持っているために、接近しすぎると安定な円運動を行えないからである。
どこまで安定に円運動できるかは、そのブラックホールの質量(大きさ)と回転の度合で決まる。
ブラックホールが全く回転していない場合、ブラックホール半径の3倍より内側では安定に円運動ができず、
シュバルツシルト半径と円盤の間に空間ができてしまう、というわけだ。
このようなブラックホールを「シュバルツシルト・ブラックホール」と呼んでいる。
******チェック3. 内縁半径を計算してみよう。******難易度 ... 易
シュバルツシルト半径は質量に比例している。
ブラックホールが1Msunなら半径3km、10Msunなら半径30kmである。
シュバルツシルト・ブラックホールの場合、もし内縁半径が90kmなら、90/3=30kmがシュバルツシルト半径だから、
ブラックホールの質量は10Msunであることが分かる。
つまり、内縁半径を観測すれば、ブラックホールの質量が分かるのである。
******チェック4. ブラックホール質量を計算してみよう。******難易度 ... 易
2.3 内縁半径を観測するには?
では内縁半径はどうやったら分かるのだろうか?黒体放射をしている「ある大きさ」の物体が「ある温度」になると、「ある光度」になる。
ゆえに温度と光度が分かれば、大きさが分かる。
降着円盤の場合、大きさとは内縁半径のことである。
ではいよいよ次の章から実際のX線データを触ってみよう。
これから触るデータには「温度」と「光度」の情報が含まれている。
つまり大きさ(内縁半径)が分かるのである。
データから内縁半径を導き出し、ブラックホール質量を計算しよう。
はたしてその質量はペアの恒星の動きから求めた質量と一致するのだろうか?
3. ブラックホールのX線データ
3.1 対象天体:大マゼラン雲(LMC) X-3
今回扱うブラックホールは、地球から約16万光年離れた「大マゼラン雲」という銀河の中にある、X-3というブラックホールだ。大マゼラン雲は英語で Large Magellanic Cloud というので、略して LMC と呼んだり する。
X線で3番目に発見されたから X-3 というのである。
だからこのブラックホールは LMC X-3 という名前で呼ばれる。
ペアの恒星の動きから、LMC X-3の質量は6〜9Msunだと分かっている。
1.5節の説明通りならば、この質量は白色矮星や中性子星では説明できない。
この天体がブラックホールであることはほぼ間違いないだろう。
3.2 観測衛星:ロッシX線望遠鏡 (Rossi X-ray Timing Explorer)
X線データを取るには観測衛星が必要である。観測衛星にはそれぞれの特色がある。
今回用いるロッシX線望遠鏡は何度も何度もLMC X-3を観測しているので、時間変化を詳しく調べるのに適した衛星だ。
いきなり大量のデータを扱うのは大変なので、最初はひとつのデータを触ってみよう。
3.3 データをダウンロードする
さっそくLMC X-3のデータをダウンロードしよう。これは2005年6月26日に観測されたものである。
エクセルで今のファイルを開いてみよう。
このようなものが得られるはずである。
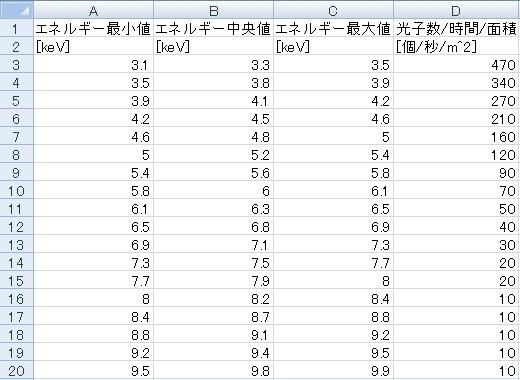
例えばA3には「3.1」、B3には「3.3」、C3には「3.5」、D3には「470」と書いてある。
これは「3.1〜3.5keV のエネルギーを持った光子が、1秒間、1m2あたりに470個得られた」ということを表している。
こういうものをスペクトルと呼ぶ。
スペクトルとは、どんなエネルギーを持ったX線がどれくらい来ているか、を表すものである。
3.4 スペクトルを見る
先ほどの表を見るとエネルギーが低い光子の方が多いようである。しかし表で見てもいまいちよくわからない。グラフにして一目で分かるようにしたいものだ。
プリンターがあって印刷ができる人は、実際に自分の手でグラフにしてみることをお薦めする。
次のグラフ用紙を印刷し、どのようなスペクトルが得られるのか確かめてみよう(印刷用pdf)。
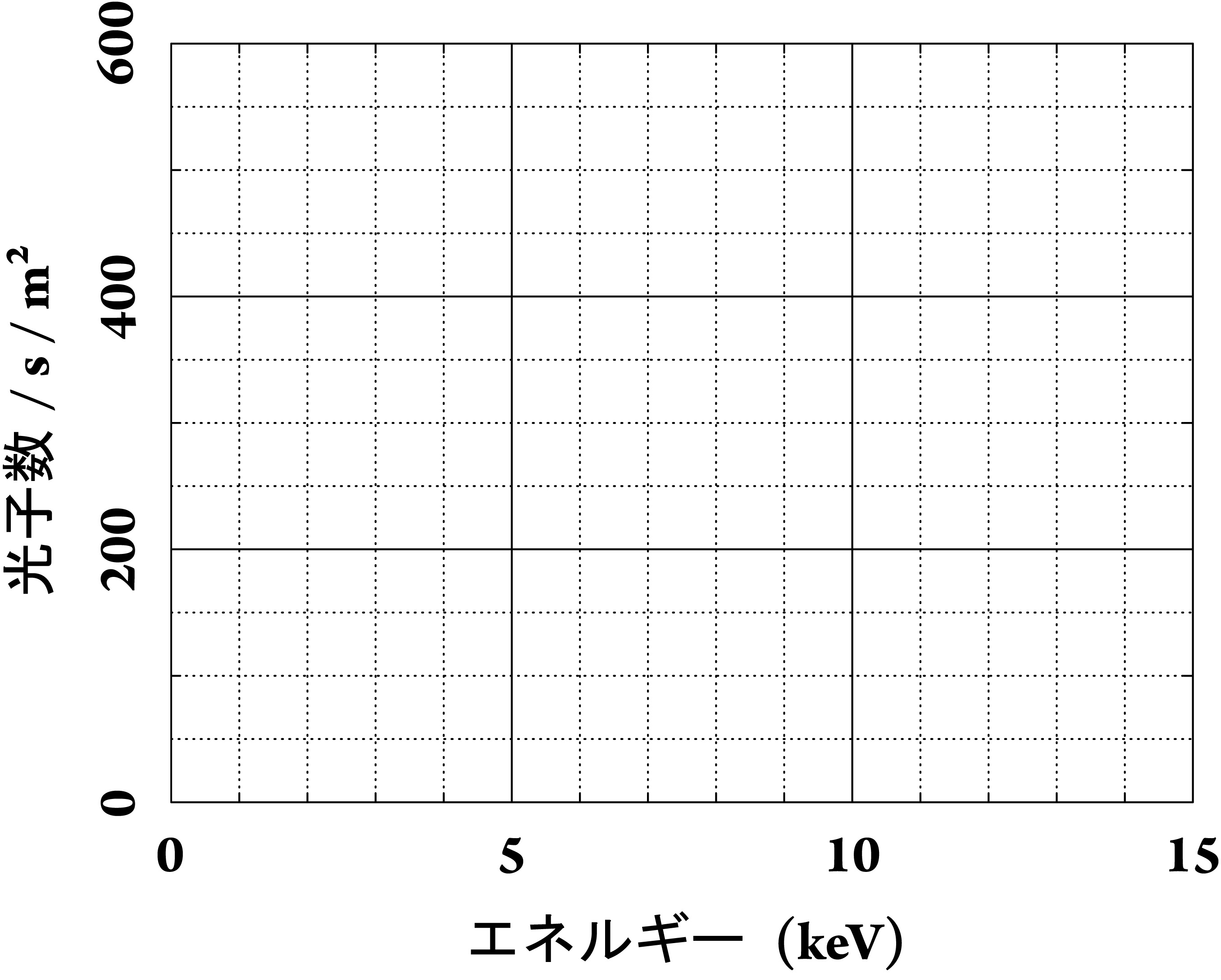
印刷ができない人のために、エクセルでこの表をグラフにする方法も載せておく。
(※ ここでの例は excel 2007 を使用している)
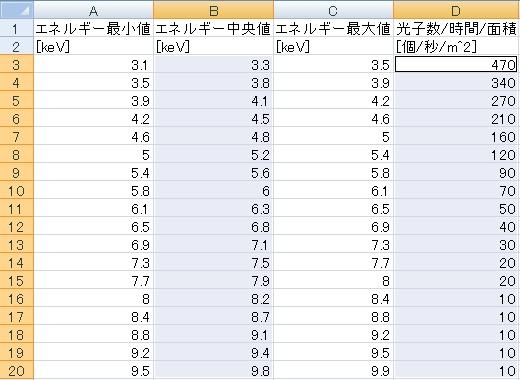
まず次の図のように選択する。
このように選択するには、まずCtrlキーを押しながらを「B3」で左クリックを押しっぱなしにする。
そしてどちらも押しっぱなしのまま「B20」までマウスを移動させると、B3からB20までが選択される。
Ctrlキーを押した状態のまま、次は「D3」で左クリックを押しっぱなしにする。
そして「D20」までマウスを移動させると、図のような選択が可能になる。
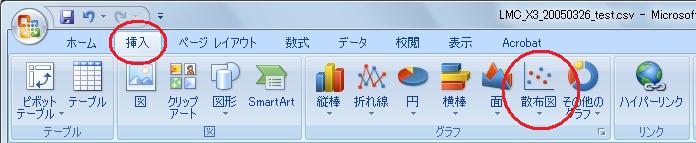
次に「挿入」を選んで「散布図」を選択する。
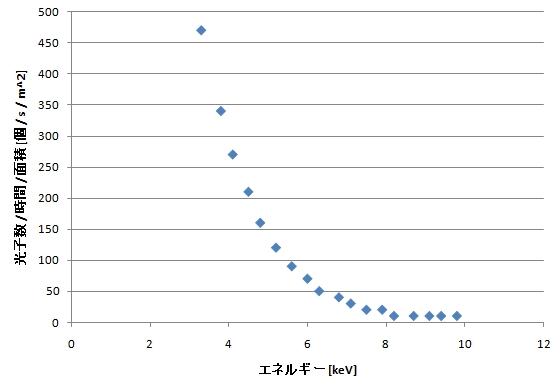
こういうスペクトルが得られれば、第一段階は終了である。
確かにエネルギーの低い光子が一番多く、エネルギーが高くなるにつれて光子がすくなくなっていく様子が見て取れる。
4. 実践 -- X線データからブラックホール質量を求める
ブラックホール質量の求め方を整理しておこう。まずスペクトルから「温度」と「光度」が分かる。
温度と光度が分かれば、「大きさ(内縁半径)」が分かる。
内縁半径が分かれば、「シュバルツシルト半径」が分かる。
そしてシュバルツシルト半径が分かると、「ブラックホール質量」を求めることができる。
具体的にひとつひとつやってみよう。
ただし注意しよう。これからする計算は、ある2つのことを仮定している。つまり、
「円盤は完全な黒体放射をする」「相対論的な効果はない」
という仮定だ。
実際はこの仮定からずれているので、最終的に出てくる値は小さめになる。
内縁半径を求める段階(4.2節)でこれらの補正を行うので、頭の片隅に置いておいてもらいたい。
4.1 スペクトル → 温度と明るさ
4.1.1 温度の求め方
降着円盤の温度はエネルギーの高い光子と低い光子がどれくらいの割合で来たか、で決めることができる。この表を見てみよう。
左の列は光子数比( = 高いエネルギー[5-10keV]の光子の割合 ÷ 低いエネルギー[3-5keV]の光子の割合)であり、
右の列はそれに対応する円盤の温度である(単位はK:ケルビン)。
例えば光子数比が 0.382 のときは「高いエネルギーの光子の数は、低いエネルギーの光子の数の38.2%」であることを示し、
そのときの円盤温度は 1580万K である。
さて、では今回のデータの温度はどれくらいかを見積もってみよう。
次の図のように、まず高いエネルギー[5-10keV]の光子の数を合計する。
適当なセル(D22)で、「=SUM(D8:D20)」と入れよう。490、という結果が出力される。
同じように低いエネルギー[3-5keV]の光子の数を合計すると、1450であるらしい。
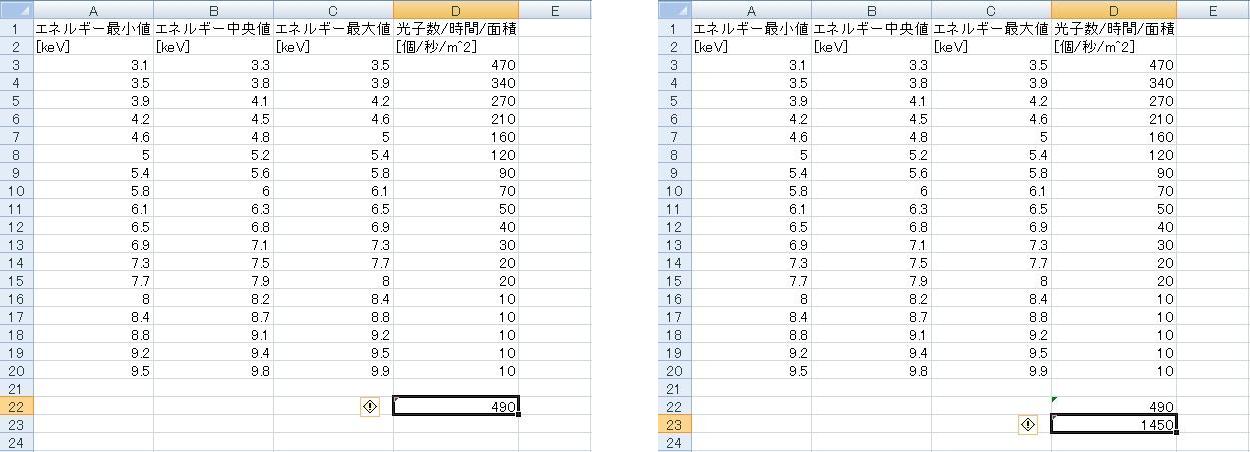
これらを割ってみよう。0.33793... という数字が出てきただろうか?
では先ほどの表の上の段でこの数字に一番近いものを探してみよう。
0.337 というものがある。これに対応する温度は1390万Kだ。
つまり今回のスペクトルは、円盤温度が約1390万Kであることを示している。
4.1.2 光度の求め方
ところで光度(明るさ)とはなんだろうか?明るいとか暗いとか、どうやって数字で表せばよいのだろう。
ここでもやはりエネルギーを使う。
たくさんエネルギーを放出すれば「明るい」というし、あまり放出しなければ「暗い」というのだ。
光度とは、1秒間にどれくらいのエネルギーを放出するか、で決まっているのである。
では今回の天体は1秒間にどれくらいのエネルギーを放出しているのだろうか?
それを知るためにまず、「1m2あたりの光度」を求めてみよう。
この量を フラックス と呼んでいる。
ざっくり言えばフラックスとは、「天体が出したエネルギーのうち、我々が望遠鏡で捉えることができたエネルギー/望遠鏡の面積」のことである。
我々が捉えるエネルギーは、天体が本当に出したエネルギーのごくごく一部でしかないので、
このフラックスをもとにして天体の本当の光度を逆算してやろうというわけだ。
具体的は 1つ1つの光子のエネルギー × 光子数 / 時間 / 面積 を計算すればよい。
次の図のように、E3のセルで「=B3*D3」と打ってみよう。
これは上の式(1つ1つの光子のエネルギー × 光子数 / 時間 / 面積)を計算しているのである。
次に全てのエネルギーについて同じことをする。
図のような数字が得られただろうか?
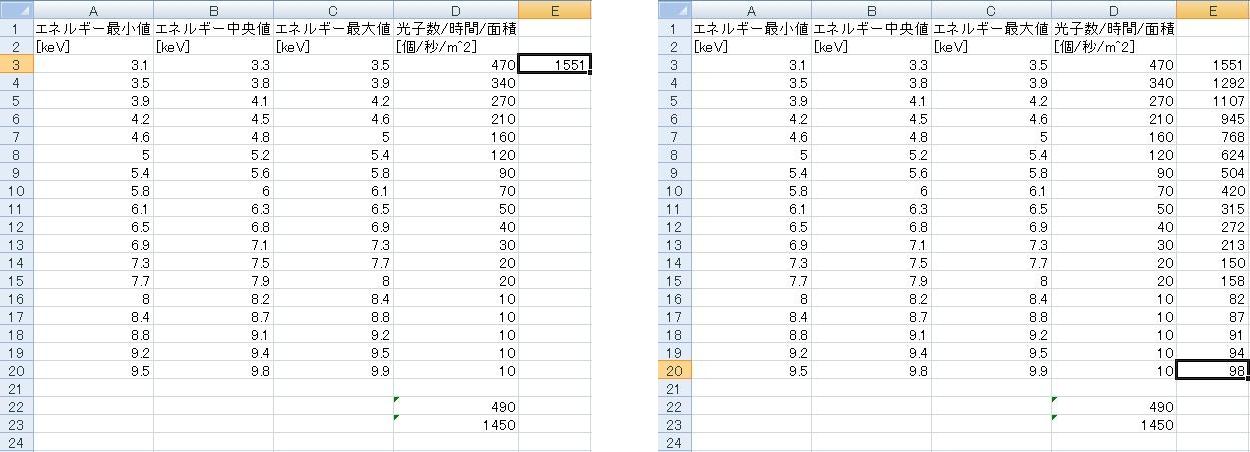
ではこれらを足してみよう。8771 という数字が出力される。
つまり今回のフラックスは 約 8771 keV/s/m2 だというわけだ。
単位を keV から J に直そう。
1 keV = 1.6 × 10-16 J だから、約 1.4 × 10-12 J/s/m2 が正解である。
フラックスは分かった。 では天体の本当の光度はどれほどだろうか?
光度Lを求めるときは、フラックスf と 距離D と 円盤の傾きi を用いて次の式を計算すれば良い。
円盤の傾きはすでに約70°と分かっているのでそれを使おう。
次の値を代入し、全体の明るさLを計算してみよう。
* f = 1.4 × 10-12 [J / s / m2]
* D = 16万光年 = 1.5 × 1021 [m]
* cos i = cos 70° = 0.342
約5.8 × 1031 J/s がこの天体の光度である。
ちなみに太陽の光度は 3.8 × 1027 J/s だから、
驚くべきことにこのブラックホールは太陽の15万倍ものエネルギーを放出していることになる。
4.2 温度と光度 → 内縁半径
これで温度と光度が分かったので大きさ(内縁半径)を導くことができる。具体的にはどういう計算をすればよいのだろうか?
「黒体放射する物体の光度は温度の4乗に比例する」というステファン・ボルツマンの法則を用いる。
その法則によれば、温度T、放射面積Sの物体の明るさLは次の式によって表される。詳しくは中性子星の章を参照してほしい。
σ は初めて出てきたが、これは「ステファン・ボルツマン定数」という、ある決まった数である。
今回のような降着円盤の場合、内縁半径R*と円盤温度T*を用いて次のように変形できる。
この式を解けば良い。
内縁半径を求める形に整理してみよう。
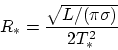
あとは計算するだけだ。単位に気を付けて、次の数を代入して内縁半径を計算してみよう。
* L = 5.8 × 1031 [J/s]
* T* = 1390万 [K] = 1.39 × 107 [K]
* σ = 5.67 × 10-8 [J / m2 / K4 / s]
最終的に 47km という値が得られただろうか?
ただしこれは本当の内縁半径ではなく、みかけの内縁半径である。
この章の最初で注意したように、この内縁半径はすこし小さめに出ている。
黒体放射と相対論的効果の補正を考慮すると、このみかけの内縁半径を1.2倍したものが本当の内縁半径になる。
つまり 47×1.2=56km がこのブラックホールの内縁半径だというわけだ。
4.3 内縁半径の考察
内縁半径が56kmだということは、内縁の直径は約110kmである。主にエネルギーを出しているのは円盤の中でもブラックホールに近い領域だけだから、
X線の放射領域はざっくり100〜200kmくらいであろう。
つまり関東地方くらいの大きさしかない。
そんな小さな領域から太陽の15万倍ものエネルギーが出ているのだ!
ブラックホールとは決して、物体を吸い込むだけの物静かな天体などではない。
降着円盤を介して莫大なエネルギーを放出する、宇宙の暴れん坊なのである。
4.4 内縁半径 → シュバルツシルト半径 → ブラックホール質量
さて、内縁半径が得られたら質量は分かったも同然である。内縁半径が 56km ということはシュバルツシルト半径は 約19km である。
つまりこのシュバルツシルト半径に対応する質量は 6〜7Msun である。
この質量はペアの恒星の動きから求めた質量:6〜9Msunと一致している。
X線から求めた質量が可視光線から求めた質量と矛盾がないことからも、やはりLMC X-3はブラックホールである可能性が高い。
5. 発展 -- 多数のデータからブラックホールの証拠を得る
5.1 質量が変化しないことを確認する
4章では確かに太陽質量の6〜9倍という値と矛盾のない質量を得た。しかしこれはひとつのデータしか使っていない。偶然そうなったとは言えないだろうか?
偶然でないことを確かめるには、多数のデータを用いるのが最も簡単で確実である。
ロッシX線望遠鏡は何度もLMC X-3を観測しているので、そういう作業に非常に向いている。
ここに12個のLMC X-3のデータを用意した。
この中のいくつかについて、同じ作業をしてブラックホール質量を求めてみよう。
全部やってみてもいい。
本当に太陽質量の6〜9倍という値を得ることが出来るかどうか、自分の目で確かめてもらいたい。
2005年03月23日
2005年03月26日
2005年07月26日
2005年07月29日
2005年08月11日
2005年10月11日
2005年11月12日
2005年11月30日
2005年12月03日
2005年12月10日
2005年12月19日
2006年05月18日
光度や温度が変化しても、内縁半径だけはほとんど変化しないことが確かめられただろうか?
5.2 円盤温度と光度の関係を見る
質量がほとんど変わらないことが確認できたら、最後に5.1節で得られた円盤温度と光度をこのグラフ用紙に描き入れていこう(印刷用pdf)。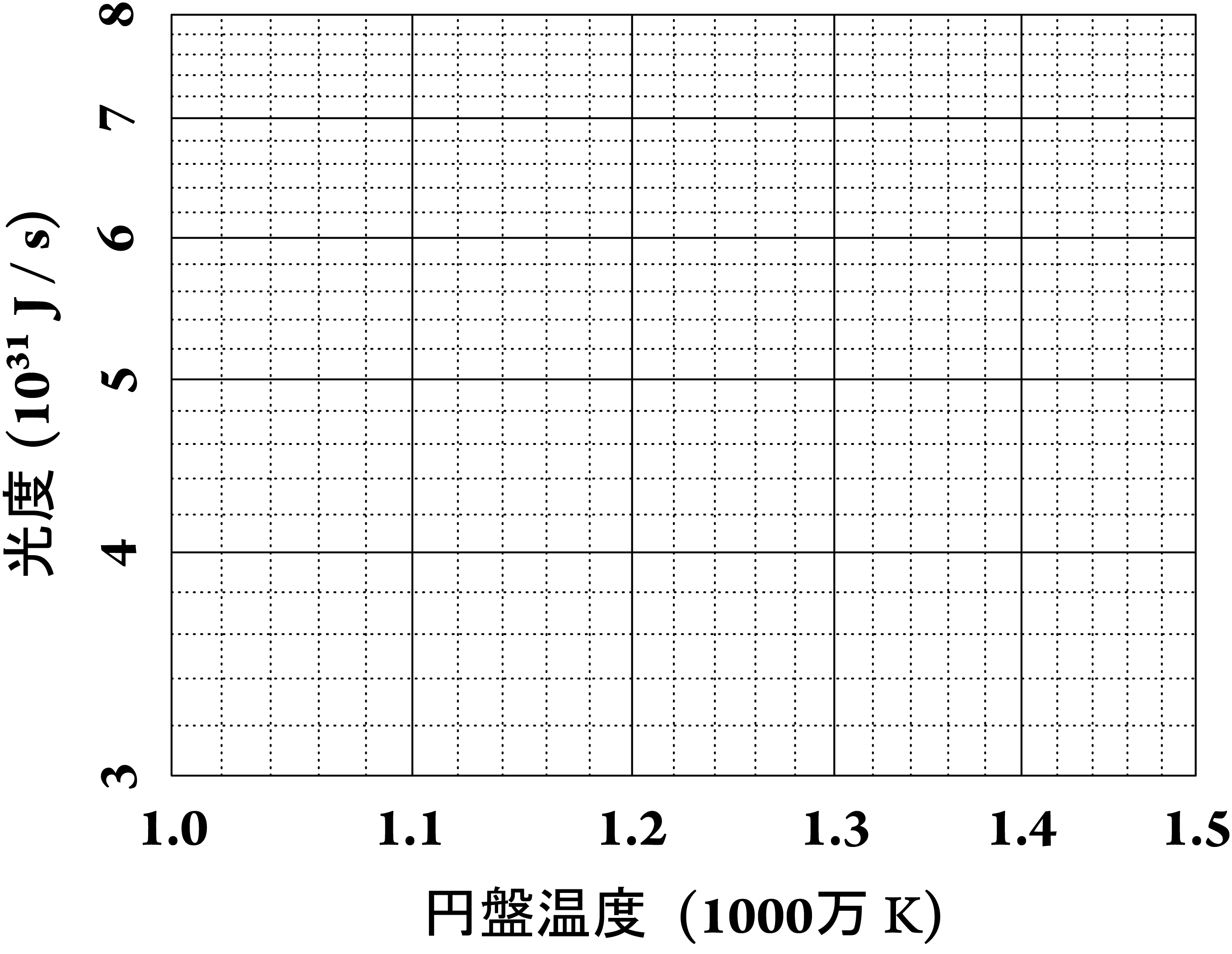
どのような図が完成するか予測できるだろうか?
これまでの学んできたブラックホールの物理は、このグラフ用紙にどのように表れるべきなのだろう?
ではすこし考えてみよう。
4.2節で次の式が出てきた。
この中のπとσは定数である。さらに、質量が一定だということはR*(内縁半径)も一定だということだ。
ということは、このように簡略化できることが分かる。
要するに「光度は円盤温度の4乗に比例する」というわけだ。
このグラフ用紙は両対数グラフなので、「傾き4の直線」という形で表れる。
実際に描き入れたとき、確かに直線になることが分かるだろう。
******小さい領域ってどれくらい?******
放射領域の大きさは変動時間から大体推測することができる。
一体どのように見積もるのだろうか?
物体は光速を超えることができないのだから、変動している物体は光速より遅いはずである。
ということは、仮に光速にものすごく近いスピードで変動していたとしても、放射領域は 変動時間×光速 より小さいはずだ。
今回の場合、0.073 s × 30万 km/s = 21900 km であるから、放射領域は最大でも大体2万kmしかない。
2万kmしかない、と書いたが、一体これって宇宙的にはどれくらいの大きさなのだろう?
適当な比較対象は、やはり身近な地球と太陽である。地球の直径は約13000km、太陽の直径は約140万kmだ。
2万kmというのは地球よりは大きいかもしれないが、太陽よりは圧倒的に小さい。
やはりこれはものすごく小さい領域だと言えよう。
こんなところから莫大なX線が出るというのは、当時は予想外で驚くべき事態であった。
戻る
***********************************************************